• 第二章 三角形的面积、边角间关系定理

思路提点

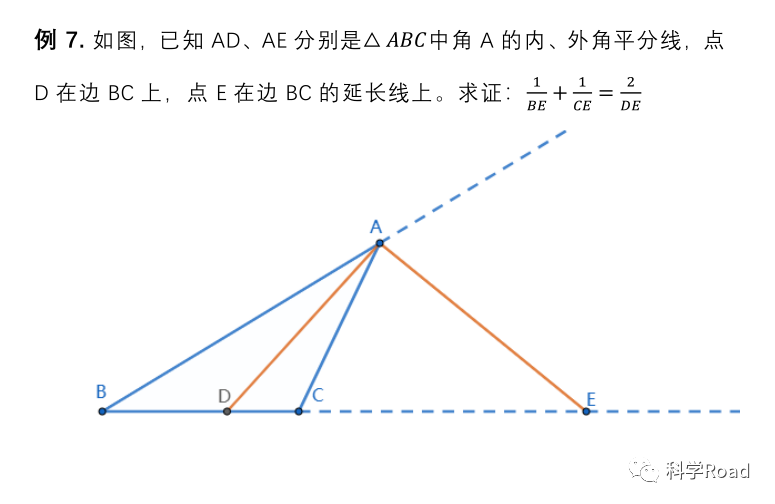
    本题主要考察三角形中对角平分线的处理，可能用到的定理有：正弦定理、余弦定理、张角定理、（外）角平分线性质定理。

• 思路1：计算线段长度

    书上的想法是设∠BAD=∠CAD=α，并用字母表示从A点出发的线段，然后用余弦定理计算BE、CE、DE，直接代入验证等式成立。

具体步骤：

（1）在设表线段时，通常我们习惯直接设三角形的边长，然而本题最终目标是落在直线BC上的线段，过A点的线段都只是过渡作用，因此为了简化计算，设AD、AE的长度一定比设AB、AC的长度更好（∠ADE=90°）；

（2）设AD=a，AE=b，可用张角定理表示出AB、AC的长度；

（3）用余弦定理表示出BE、CE、DE的长度，验证即可。

解答过程：

• 思路2：转化为角度计算

    注意到求证的等式是齐次式，可用正弦定理转化为角度的关系式，然后利用三角变换的恒等式证明。

（1）设∠BAD=∠CAD=α，∠B=β，在△ABE、△ACE、△ADE中分别用正弦定理，表示出BE、CE、DE；

（2）代入验证即可。

解答过程：

• 思路3：几何法

    由三角形中角平分线的性质定理、外角平分线的性质定理容易证明。

解答过程：

方法小结

• 方法一：以边长为主，直奔主题，计算量相对较大，适合对三角形内的线段计算十分熟悉的同学；
• 方法二：以角度为主，间接转化，计算量小，适合熟悉三角函数恒等变换的同学；
• 方法三：纯几何法，简洁明了，涵盖本章必须掌握的定理：（外）角平分线性质定理。

知识拓展

    事实上，到B、C距离比例相等的点均在同一个圆上，对平面上任一点P，如果PD平分∠BPC，则P在以DE为直径，以DE中点O为圆心的圆上，我们把这个圆称作阿波罗尼斯圆，简称阿氏圆。

    感兴趣的同学可以尝试证明定理：

    平面内到两个定点的距离之比为常数k(k≠1)的点的轨迹是圆