数学奥林匹克小丛书--初中卷:三角形的外心

正文
第七章 三角形的四心
接下来介绍外心:
定义
性质1
性质2

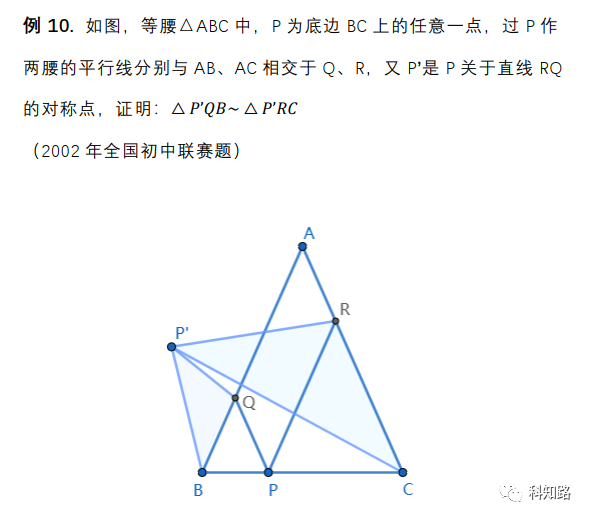
很容易发现要证的△P’QB和△P’RC都是等腰三角形,等腰三角形证明相似只用证明顶角相等,那么此题就转化为一个处理角度代换的问题。



正文
第七章 三角形的四心
接下来介绍外心:


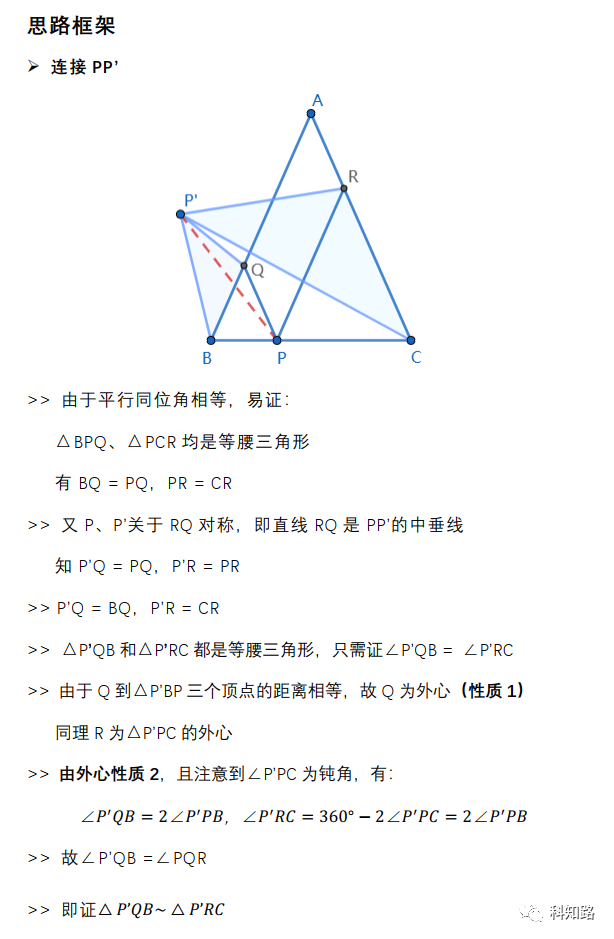
很容易发现要证的△P’QB和△P’RC都是等腰三角形,等腰三角形证明相似只用证明顶角相等,那么此题就转化为一个处理角度代换的问题。



发布于 2024-04-23 13:10
全部 0条评论