数学奥林匹克小丛书--初中卷：等腰直角三角形
-
-
上海小升初 这家伙很懒，还没有设置简介
0 人点赞了该文章 · 187 浏览
本系列参考教材为小蓝本：数学奥林匹克小丛书（第三版）初中卷
正文
第十章 等腰三角形
本节我们学习等腰三角形的构造，其中等腰直角三角形尤为特殊，在出现直角或者45°特殊角的问题中我们往往通过构造或者证明等腰直角三角形可以取得不错的结果。
性质：
下面看一个例子：
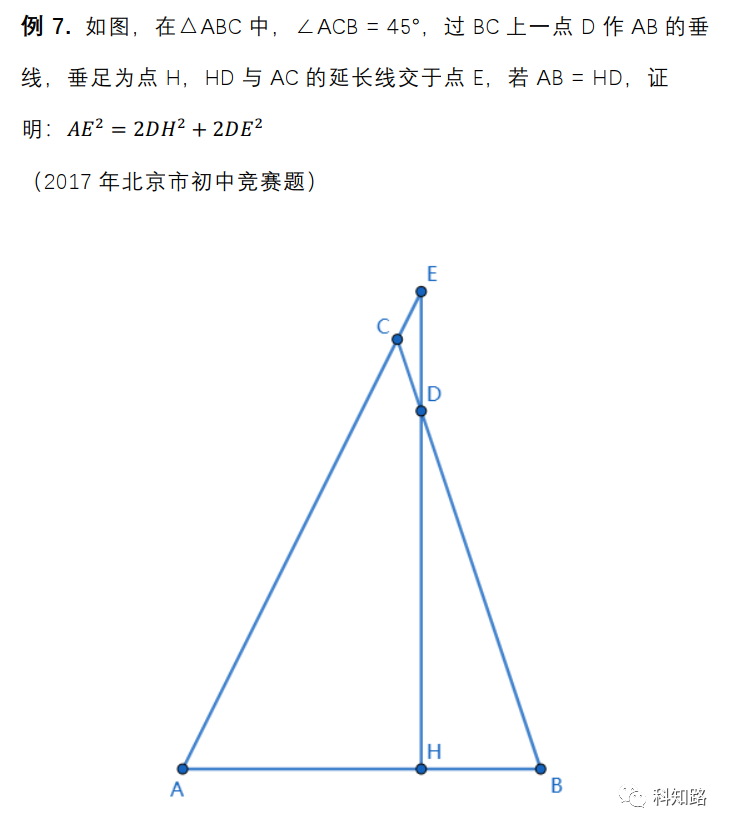
下面来看具体思路：
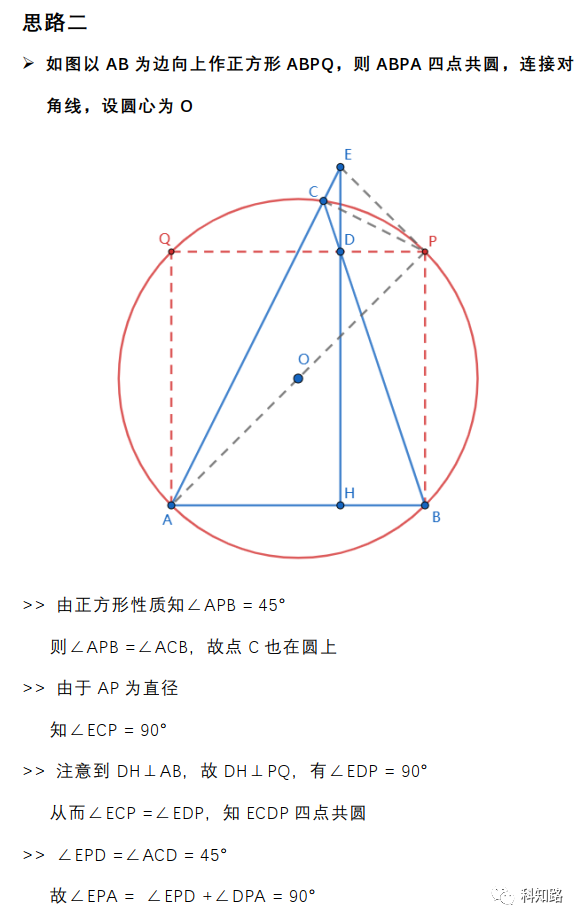
2、辅助线构造思路：
法一的思路是结合DH=AB条件构造全等，由于45°的介入呈反K形；
法二的思路则是从∠C=45°知晓C点的轨迹在一个圆上，我们通过构造出这个圆巧妙地解决问题，需要同学对四点共圆的知识比较熟悉
全部 0条评论