这个寒假要写基金申请本子，杂事也多，没有时间写长篇大论了，只能抽空讲讲题。

下面两道题是高思导引三年级有关计算的。如果想激发娃的兴趣，提升计算能力，那可以玩一玩美国的数学跳棋《寒假带娃玩什么？美国数学跳棋，专注运算能力！》，玩法多样，适合不同年龄的娃。

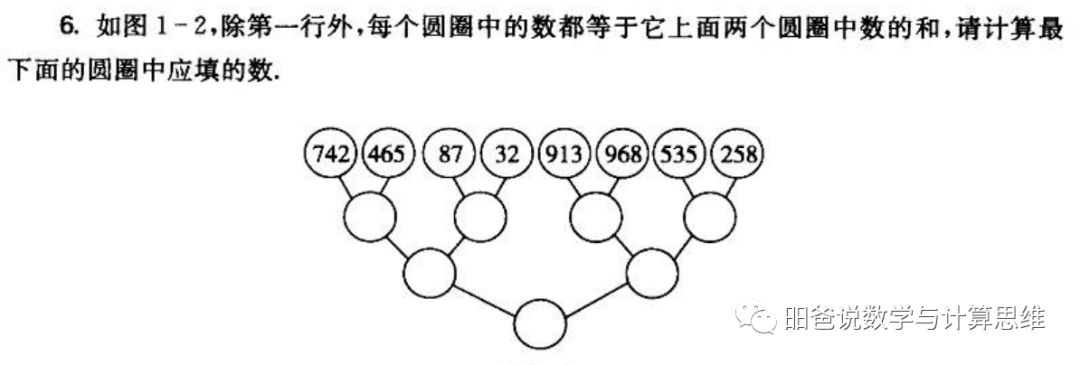
这个题，当然可以老老实实一个个圆圈加起来计算，但这样计算的话，工作量太大。其实这题最重要考察两点：

（1）整体思维

（2）交换律

所谓整体思维，就是通过观察可以发现，最后那个圆圈就是上面八个数之和，所以，我们就没有必要两个两个地按部就班计算了。

意识到最后的结果就是742+465+87+32+913+968+535+258后，就可以利用加法交换律，将原来的计算变成：

(742+258)+(465+535)+(87+913)+(32+968)=4000

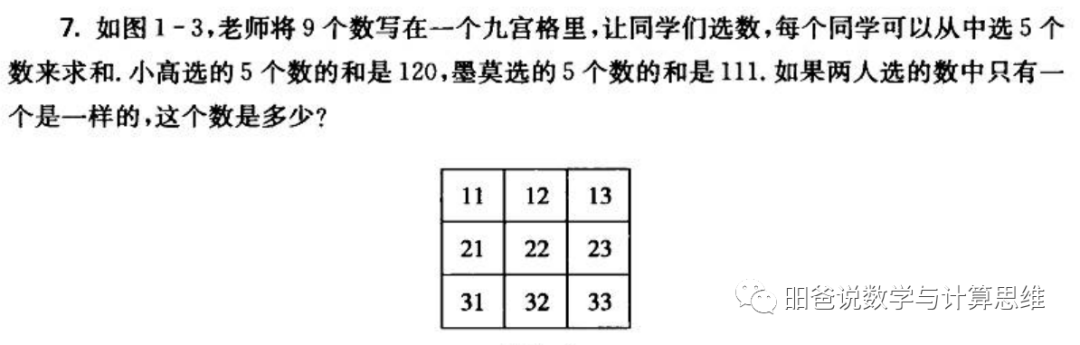
这个题，首先要把问题的条件读清楚，我们不妨罗列一下：

（1）一共有9个数，而且这9个数很有特点；

（2）小高和墨莫各选了5个数；

（3）小高和墨莫选的数有1个相同；

（4）小高的5个数之和为120，墨莫的5个数之和为111。

有的人一看到这个问题就会去猜小高选了哪5个数，它们的和才能是120，墨莫又选了哪5个数，和才能是111。

比如 31+32+33+11+13=120，31+22+33+21+13=120。我们发现，其实有很多组都满足和为120的要求，比如把其中一个十位的3换成2，把另一个2换成3或者把另一个1换成2。

因此，去枚举所有的可能性有点不现实。

我们不妨换个角度，问题要问的是两个人选的一样的数是哪个。假如选的是11，那会怎样？

由于小高和墨莫只有这一个数相同，所以两个人选的另外四个数互不相同，那只能是12，13，21，22，23，31，32，33。不管谁选了哪4个数，它们的和总是不变的(又是整体思维)，为12+13+21+22+23+31+32+33，再加上两个11，最后两个人选的10个数之和为209≠120+111。

上面的分析其实表明：两个人选的10个数必须覆盖所有的9个数，其实就是所有9个数再加上两人同时选中的那个数。

由于9个数的和为36+66+96=198，而两个人的10个数之和为120+111=231，因此两个人共同选的那个数就是231-198=33。