2024年希望数学培训题题六年级详细解析与简评

解析部分

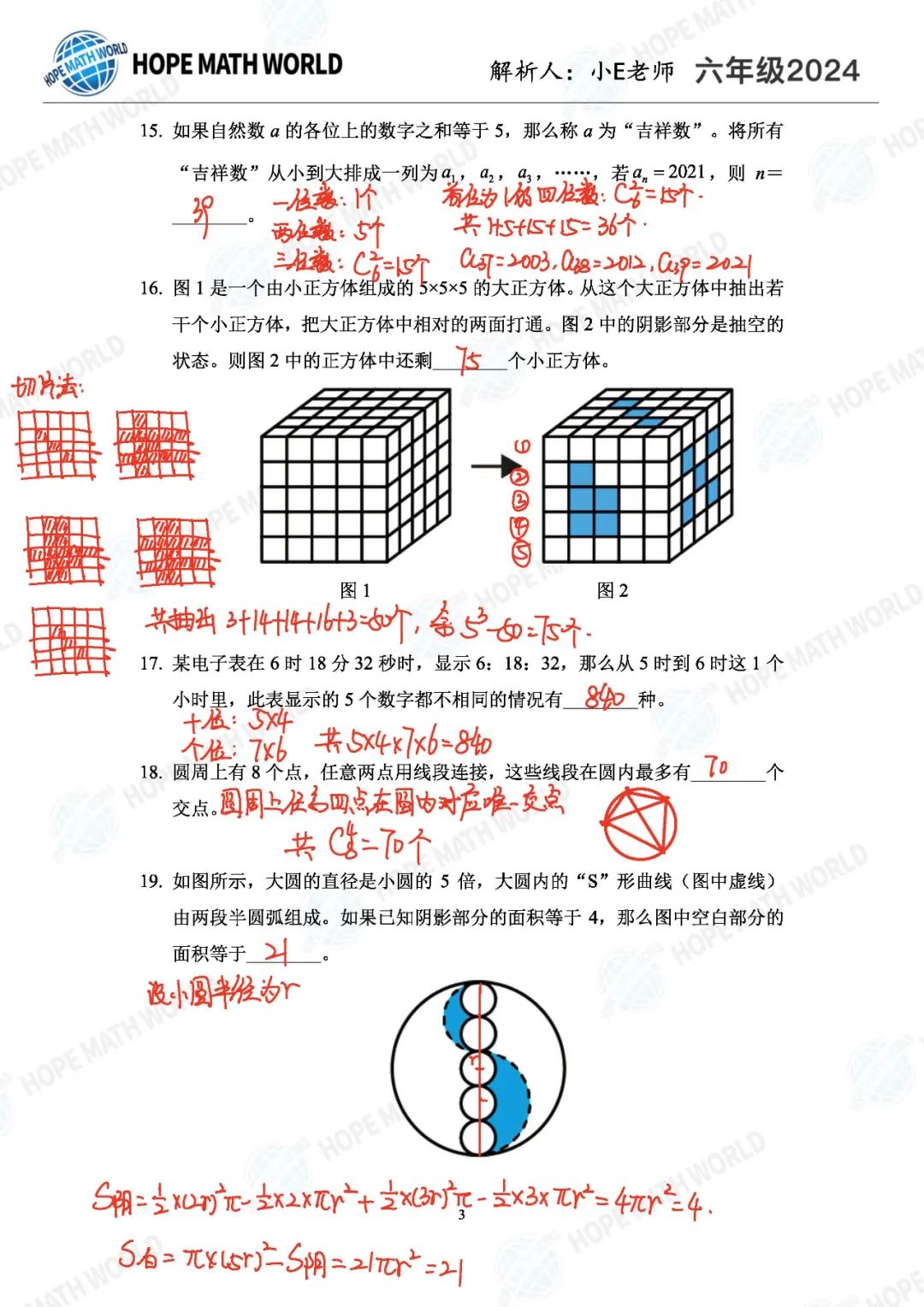

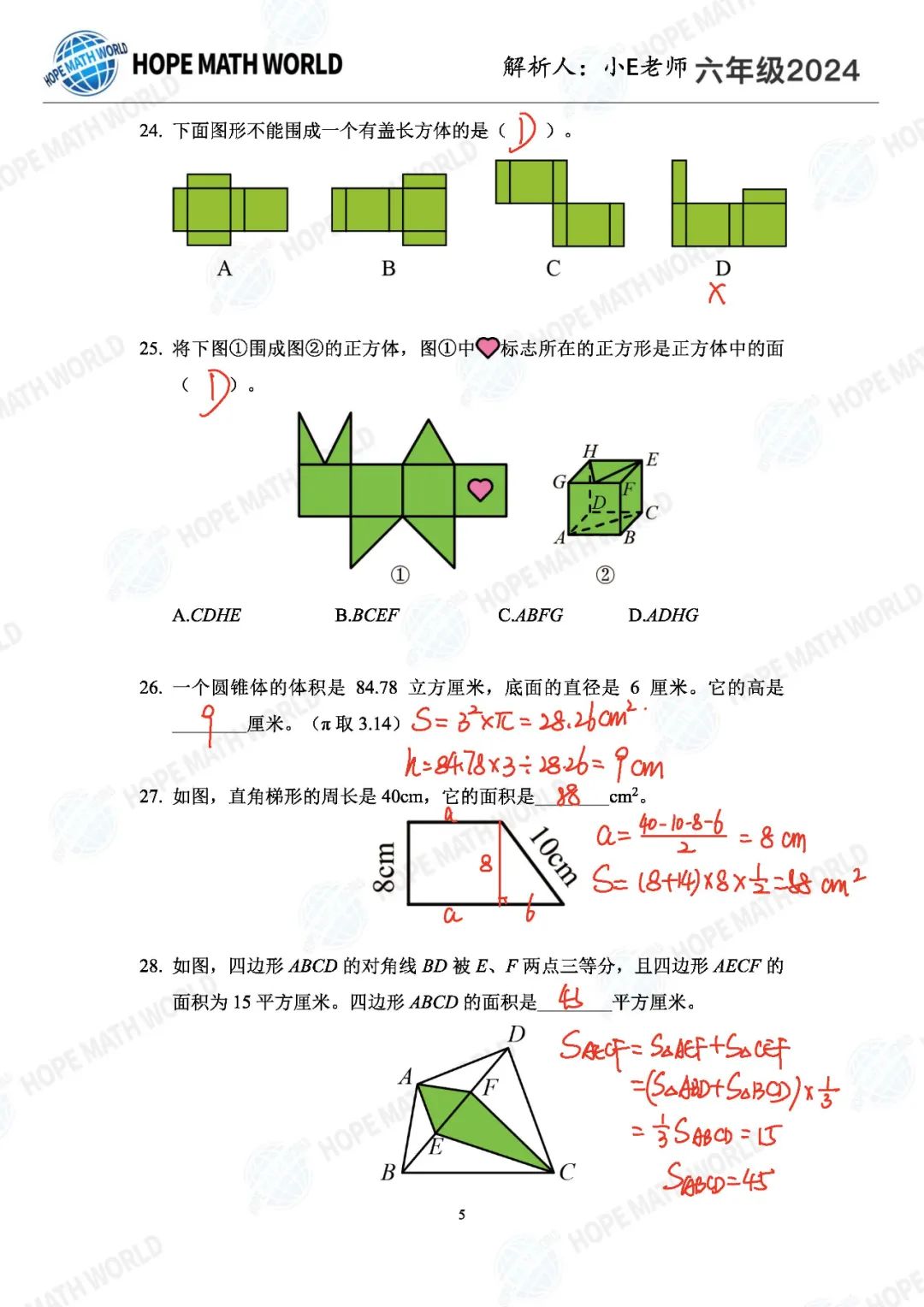










简评部分
六年级的题目,码题痕迹过重,难度过于参差不齐。
简单说一下我认为值得关注的几个题。
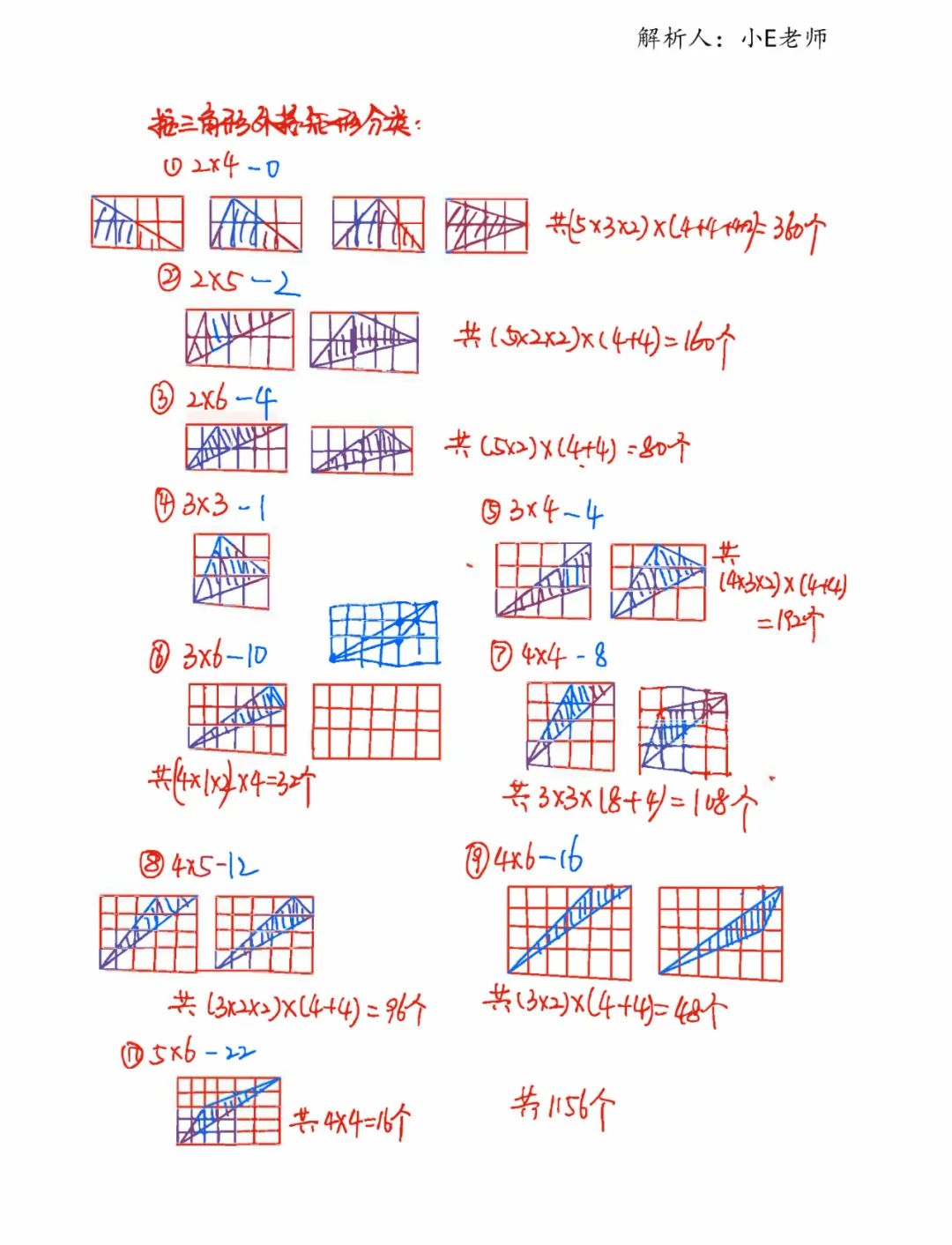
Q14是一个特别反人类的题,格点图形计数的核心思路,是按照三角形外接的矩形将三角形形状分类枚举,然后通过数矩形个数来数出三角形。但是6×6中可能存在的情况实在过多了。方法本身需要掌握,但我不认为这个是孩子能解决的。
Q21来自2020年华杯,核心是正六边形中的一半模型,属于正多边形几何里常考的知识点。
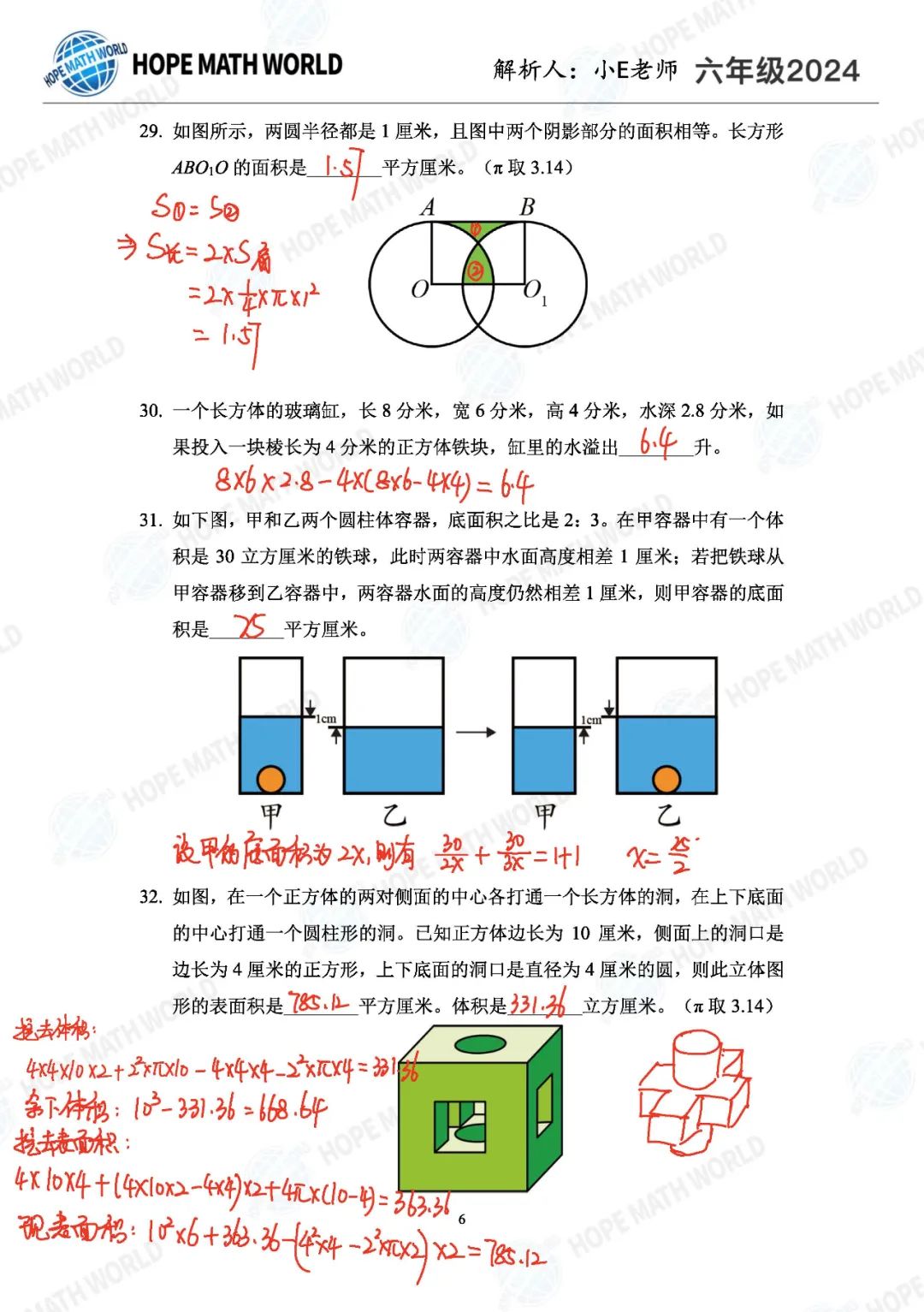
Q31是一个差量分析的思路,通过水面高度变化量列出方程得到答案,思考方式有一定参考性。
Q32这种挖洞问题,计算表面积变化最简单的方式,是先求出被挖去图形的总表面积,其中本来不在表面的是增量,本来就在表面的是减量,所以可以得到公式:表面积增量=挖去图形表面积-2×原表面积减少量。
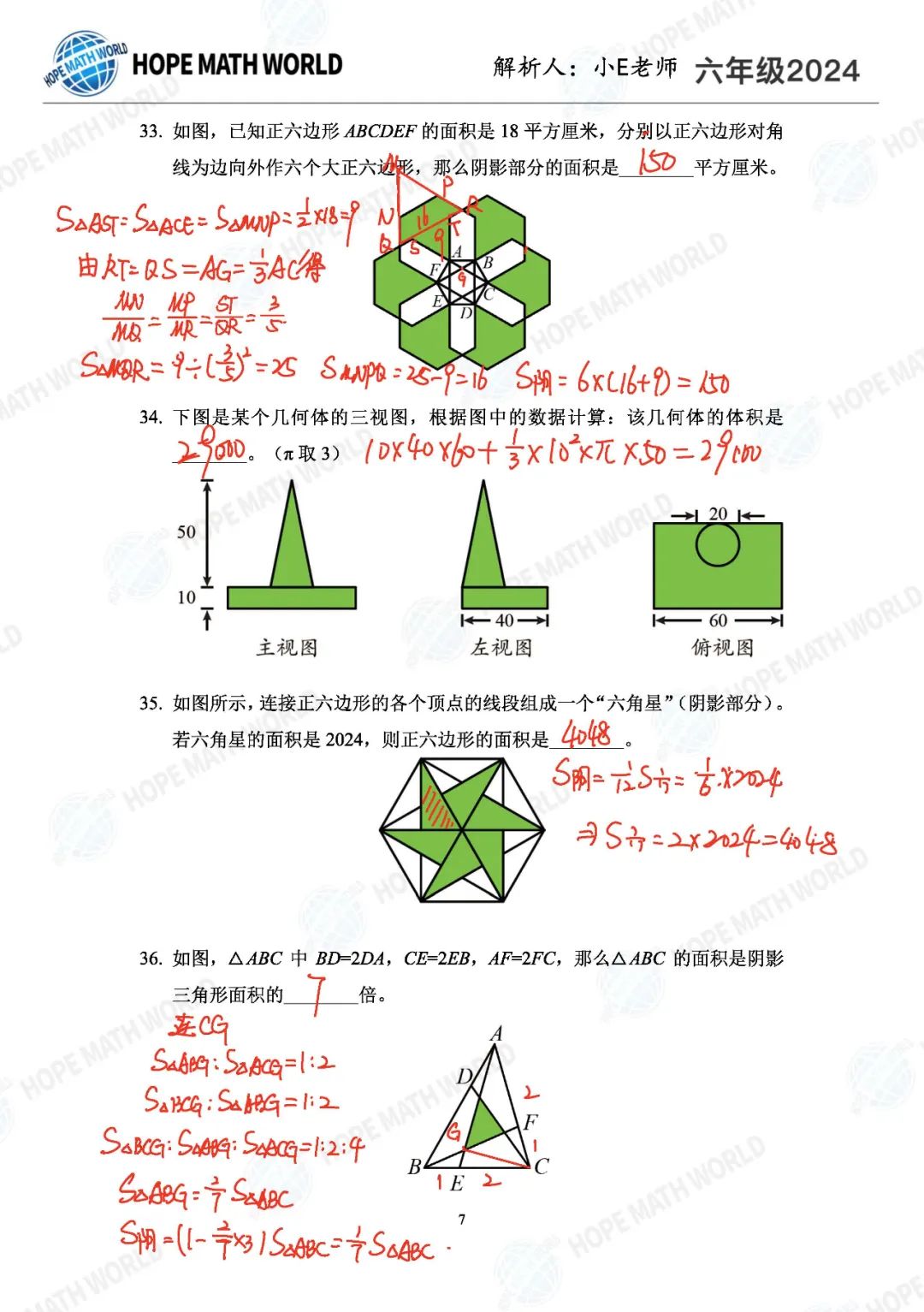
Q33是个比较难的正多边形几何,需要综合应用相似模型、全等和鸟头模型去解决。
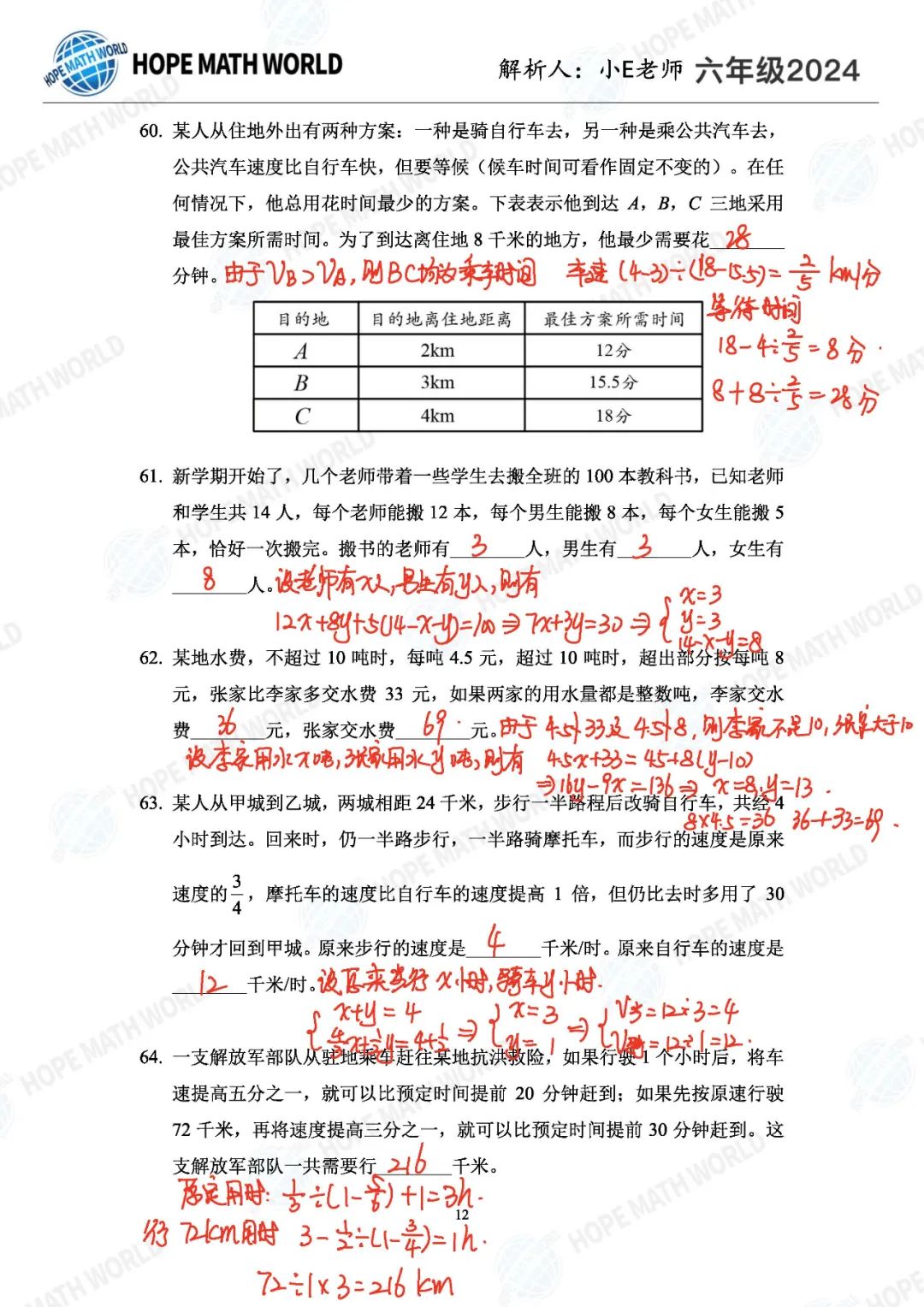
Q40不那么容易想到。由于平均速度等于速度和,证明两船的行驶方向始终保持相反,即两船同时调头,这个突破口比较隐蔽,但见过类似问题的孩子应该容易想到。
Q41可以用设而不求的方式列方程求解,也可以直接利用整体平均的结论去做,一个比较经典的问题。
Q42的题面不严谨,实际上边长只有唯一解。最早版本的这道题就是错的,一直延续至今。
Q49是个导引5星题,原解析比较繁琐,给出的这个做法简洁一些。
Q66在类似的考察最大奇因数问题中算是最简单的了,相似但更难的题还是有很多,偶尔会见到。
Q68算是比较有意思的数阵图最值,还是要把握数和、线和、重合数的关系。
Q74本身比较无聊,属于典型的纸老虎问题,要求孩子面对看似复杂的题时有动笔的勇气。
Q79也是个导引题,看起来是逻辑推理,其实本质是数独,做好转化就很简单。
Q86是个数论方程变形题,对小学生可能有一定难度。
Q94还是老生常谈的看到质数就想到奇偶性分析,以及最基础的因式分解。
Q98因为是6的倍数,所以存在简便算法,不含6且是6的倍数的数,可以任意填写个位和十位,然后百位根据个位和十位的余数,补位039/147/258。这一性质对于3和9的倍数都适用。
Q99需要先分析连续10个数中最多有几个奇数,再通过平均数计算找到答案,平均的思想很重要。
其他题目都是常规题或者比较无聊的题目。



全部 0条评论