2021AMC12解读

AMC12有11道和对应的10卷相同(其中10道属于1-20题),所以AMC10能做对20道的可以直接挑战12,晋级AIME的机会更大。——要补充的只是一些复数和立体几何知识。
所以我们就来看下AMC12到底考些什么吧。这里对A和B卷也只讲前20道题,其中和10相同的不再重复,请回看:
AMC12 A
Problem1 (代数/计算)
What is the value of 21+2+3-(21+22+23)?
(A)0 (B) 50 (C) 52 (D) 54 (E) 57
提示:直接计算即可。
Problem 2 (代数/计算)
Under what conditions does (a2+b2)1/2 =a+b hold, where a and b are real numbers?
(A) It is never true.
(B) It is true if and onlyif .
(C) It is true if and onlyif .
(D) It is true if and onlyif and .
(E) It is always true.
提示:显然a+b<0时不成立,a=b=0时成立,可直接排除A、B、E,选择D。
Problem 3
The sum of two natural numbers is 17,402. One of the two numbers is divisible by 10. If the units digit of that number is erased, the othernumber is obtained. What is the difference of these two numbers?
(A)10,272 (B)11,700 (C) 13,362 (D) 14,238 (E) 15,426
(同AMC10A Problem 3)
提示:快捷做法,两个数个位数为0和2,相减必为8。
Problem 4
(同AMC10A Problem 7)
Problme 5
(同AMC10A Problem 8)
Problme 6 (古典概率)
A deck of cards has only red cards and black cards. The probability of a randomly chosen card being redis 1/3. When black cards are added to the deck, the probability of choosing red becomes 1/4. How many cards were in the deck originally?
(A)6 (B) 9 (C) 12 (D) 15 (E) 18
提示:m/(m+n)=1/3,m/(m+n+4)=1/4。或考虑开始红:黑=1:2,后来变成1:3,即增加的4张牌等于开始的1/(1+2)。
Problem 7
(同AMC10A Problem 9)
Problem 8 (数列递推公式)
A sequence of numbers is defined by D0=0, D1=0, D2=1,
and Dn=Dn-1+Dn-3 for n≥3.
What are the parities (evenness or oddness) of the triple of numbers (D2021, D2022, D2023), where E denotes even and O denotes odd?
(A)(O, E, O) (B)(E, E, O) (C) (E, O, E) (D) (O, O, E) (E) (O, O, O)
提示:计算前10项左右,可以发现奇偶性以7为周期变化。所以所求三项的奇偶性等于第5到7项。
Problem 9
(同AMC10AProblem 10)
Problem 10
(同AMC10AProblem 12)
Problem 11 (坐标变换)
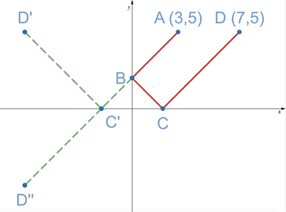
A laser is placed at the point (3, 5). The laser bean travels in a straight line. Larry wants the beam to hit and bounce off the y-axis, then hit and bounce off the x-axis, then hit the point (7,5). What is the total distance the beam will travel along this path?
(A) 2√10 (B) 5√2 (C) 10√2 (D) 15√2 (E) 10√5
解答:画出等“距”路径A-B-C’-D’’,D’’=(-7, -5),求AD’’即可。
Problem 12
(同AMC10AProblem 14)
Problem 13 (复数极坐标)
Of the following complex numbers, which one has the property that z5 has the greatest real part?
(A)-1 (B)-√3+i (C) -√2+i√2 (D) -1+i√3 (E) 2i
解答:A、E可直接求出一为负数一为0。B、C、D化为r(cosθ+isinθ)形式,r都为2,θ分别为5π/6、3π/2和2π/3。则比较π/6、7π/2和4π/3的cos即可。
Problem 14 (对数)
What is the value of
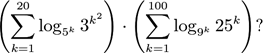
(A)21 (B) 100log53 (C) 200log35 (D) 2,200 (E) 21,000
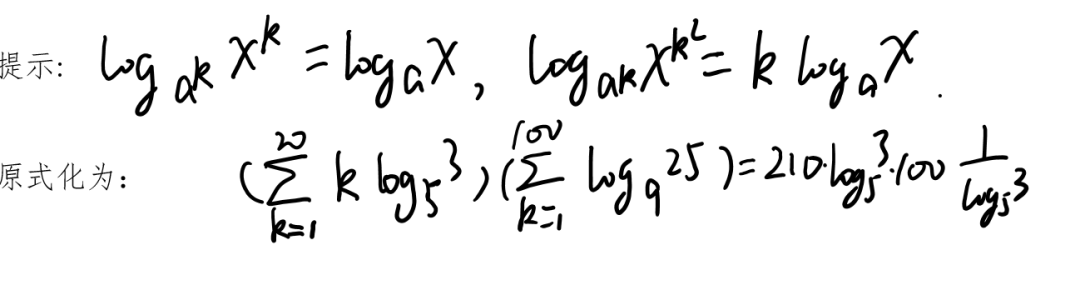
Problem 15 (组合)
A choir direction must select agroup of singers from among his 6 tenors and 8 basses. The only requirements are that the difference between the number of tenors and basses must be a multiple of 4, and the group must have at least one singer. Let N be the number of different groups that could be selected. What is the remainder when N is divided by 100?
(A)47 (B) 48 (C) 83 (D) 95 (E) 96
直接计算法:设选择m个tenor,n个bass,分别考虑m=0到6,比如m=0时,n可以选择4和8,即有C(6, 0)(C(8, 4)+C(8, 8))种可能。
高级方法(未必更快):计算生成函数
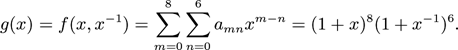
则要求的是4|(m-n)时对应的值,计算g(i)+g(-i)+g(1)+g(-1),即然后扣除m=n=0,即得到4095。
Problem 16
(同AMC10A Problem 16)
Problem 17
(同AMC10A Problem 17)
Problem 18
(同AMC10A Problem 18)
Problem 19 (三角函数)
How many solutions does the equation
sin(π/2*cosx)=cos(π/2*sinx) have in the closed interval [0,π] ?
(A)0 (B) 1 (C) 2 (D) 3 (E) 4
提示:π/2*cosx和π/2*sinx都在arcsinx定义域内,
所以π/2*cosx=arcsin(cos(π/2*sinx))=π/2-π/2*sinx,即sinx+cosx=1。
Problem 20 (圆锥曲线)
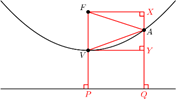
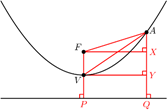
Suppose that on a parabola with vertex V and a focus F there exists apoint A such that AF=20 and AV=21. What is the sum of all possible values of the length FV
(A)13 (B) 40/3 (C) 41/3 (D) 14 (E) 43/3
提示:画出抛物线的准线,设FV=V到准线距离=d,A的两种可能如下,可以列出de的方程:212-(20-d)2=202-(2d-20)2,即3d2-40d+41=0。
Problem 21
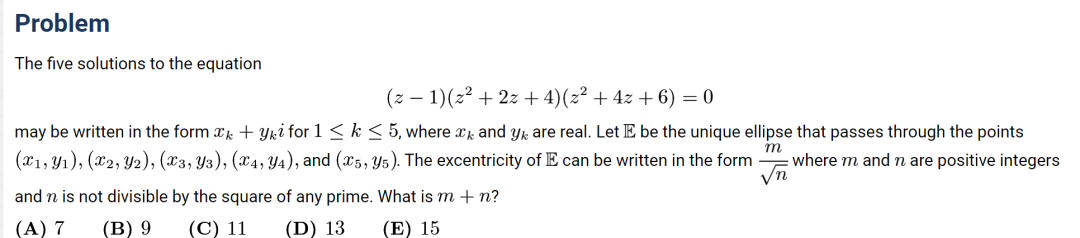
Problem 22
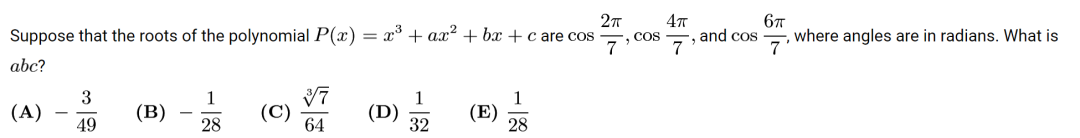
Problem 23
(同10A Problem 23)
Problem 24
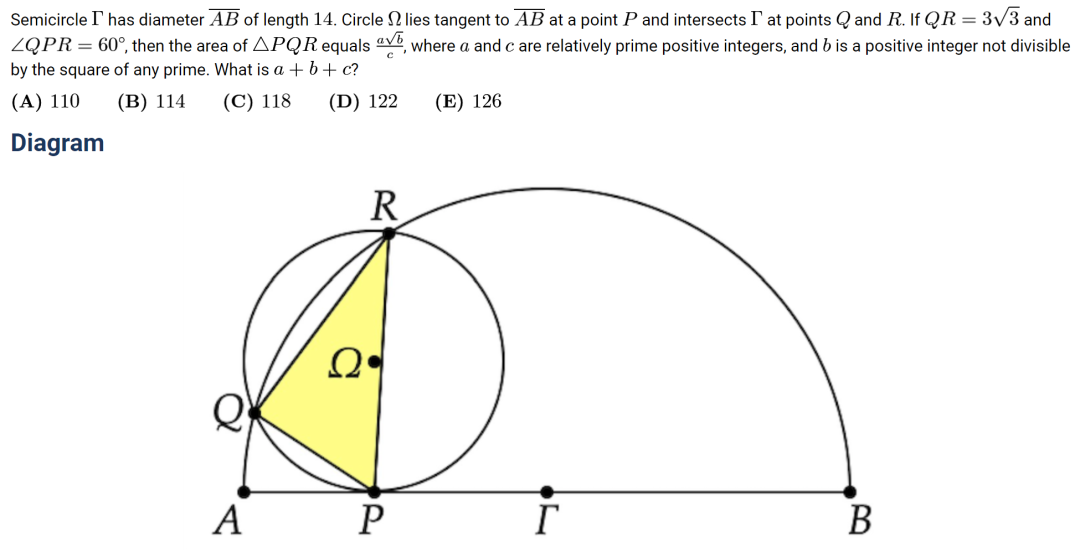
Problem 25
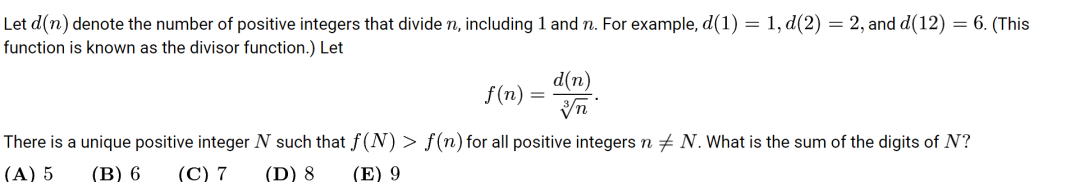
参考答案:
B D D D E
C D C C E
C A B E D
C D E C B
A D D D E
AMC12 B
Problem 1
(同10B Problem 1)
Problem 2
(同10B Problem 4)
Problem 3 (连分数)
Suppose
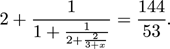
What is the value of x?
(A)3/4 (B) 7/8 (C) 14/15 (D) 37/38 (E) 52/53
提示:可直接分步计算,第一步先左右各减去2,得到(1+1/(2+2/(3+x)))=53/38,依次进行。
Problem 4
(同10B Problem6)
Problem 5
(同10B Problem9)
Problem 6
(同10B Problem10)
Problem 7
(同10B Problem12)
Problem 8
(同10B Problem14)
Problem 9 (对数)
What is thevalue of
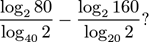
(A)0 (B) 1 (C) 5/4 (D) 2 (E) log25
提示:log280/log402-log2160/log202=log280*log240-log2160*log220=…
Problem 10 (数论)
Two distinct numbers are selected from the set {1, 2,3, 4, …, 36, 37} so that the sum of the remaining numbers is the product of these two numbers. What is the difference of these two numbers?
(A)5 (B) 7 (C) 8 (D) 9 (E) 10
提示:设减去的两个数是x和y,则703-x-y=xy,即(x+1)(y+1)=704。
Problem 11 (Stewart Theorem)
Triangle ABC has AB=13, BC=14, and AC=15. Let P be the point on AC such that PC=10. There are exactly two points D and E on line BP such that quadrilaterals ABCD and ABCE are trapezoids. What is the distance DE?
(A)42/5 (B) 6√2 (C) 84/5 (D) 12√2 (E) 18
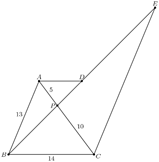
提示:利用Stewart定理,可求出BP=8√2,然后利用BPA~DPC,BPC~EPA。
Problem 12
(同10B Problem19)
Problem 13 (三角函数图像)
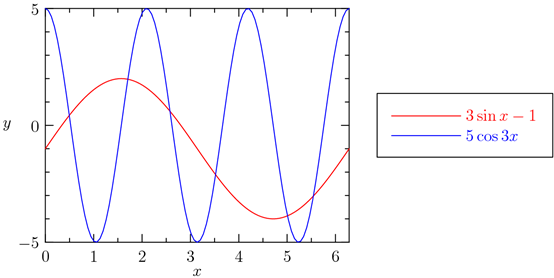
How many values of in the interval 0<θ≤2π satisfy 1-3sinθ+5cos3θ=0?
(A)2 (B)4 (C) 5 (D) 6 (E) 8
提示:画出1+5cos3θ和3sinθ的图像,求有几个交点。
Problem 14 (立体几何+不定方程)
Let ABCD be a rectangle and let DM be a segment perpendicular to the plane of ABCD. Suppose that DM has integer length, and the lengths of MA, MC, and MB are consecutive odd positive integers (in this order). What is the volume of pyramid MABCD?
(A)24√5 (B) 60 (C) 28√5 (D) 66 (E) 8√70
提示:设MA=a,MD=b,可得方程 a2+(a+2)2-b2=(a+4)2,。
化为(a-2+b)(a-2-b)-16,得a=7,b=3。
Problem 15
(同10B Problem20)
Problem 16 (多项式函数)
Let g(x) be a polynomial with leading coefficient 1(首项系数1) whose three roots are the reciprocals(倒数) of the three roots
of f(x)=x3+ax2+bx+c where 1 (A)(1+a+b+c)/c (B) 1+a+b+c (C) (1+a+b+c)/c2 (D)(a+b+c)/c2 (E)(1+a+b+c)/(a+b+c) 提示:g(x)与f(1/x)有相同根,可以推出g(x)=f(1/x)*x3/c,所以g(x)=f(1)/c。 Problem 17 (三角形和梯形) Let ABCD be an isosceles trapezoid(等腰梯形) having parallel bases AB and CD with AB>CD. Line segments from a point inside ABCD to the vertices divide the trapezoid into four triangles whose areas are 2, 3, 4, and 5 starting with the triangle with base CD and moving clockwise as shown in the diagram below. What is the ratio AB/CD? (A)3 (B) 2+√2 (C) 1+√6 (D) 2√3 (E) 3√2 提示:设该内部点到AB和CD的高分别为p和q,AB和CD长分别为r和s,则有pr=8,qs=4,同时(p+q)(s+r)=28(梯形面积)。可以解出r/s(作为一个未知数)。 Problem 18 (复数的模) Let x be a complex number satisfying 12|z|2=2|z+2|2+|z2+1|2+31. What is the value of z+z/6? (A) -2 (B)-1 (C) 1/2 (D) 1 (E) 4 提示:利用z*z共轭=|z|2,可得到下式,其中只有实部。 Problem 19 (古典概率) Two fair dice, each with at least faces are rolled. On each face of each dice is printed a distinct integer from 1 to the number of faces on that die, inclusive. The probability of rolling a sum of 7 is 3/4 of the probability of rolling a sum of 10, and the probability of rolling a sum of 12 is 1/12. What is the least possible number of faces on the two dice combined? (A)16 (B) 17 (C) 18 (D) 19 (E) 20 提示:(1)假设两个骰子面数分别为a和b(a≥b)。掷出7的组合只有6种,所以掷出10的组合有8种,推出a≥9,b=8。(2)所以总的组合数是8a种,则掷出12的组合有2a/3≤8种,即a≤12,同时3|a,a只能为9或12。(第二步亦可直接验证9是否满足。) Problem 20 (多项式除法) Let Q(z) and R(z) be the unique polynomials such that z2021+1=(z2+z+1)Q(z)+R(z), and the degree of R is less than 2. What is R(z)? (A)-z (B) -1 (C) 2021 (D) z+1 (E) 2z+1 提示:(z2+z+1)|(z3-1),用z3-1去除原式,得到余子式为z2+1,再除以(z2+z+1)。 Problem 21 Problem 22 (同10B Problem24) Problem 23 Problem 24 Problem 25 参考答案: D B A C D A C B D E D D A A D A B A B A D B A A E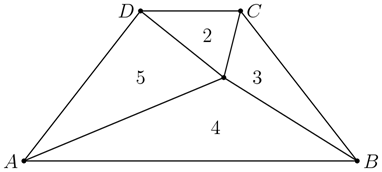
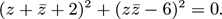





全部 0条评论