
有计划参加今年的AMC12的学生,从暑假开始就必须开始做备赛规划了。我近期将挑选几道AMC12真题做一些分析和点评,希望能对大家有所启发和思考。
这个系列一共写了七篇文章,目的并不在于全面地介绍AMC12的情况,而更多地是反映我个人的喜好和感受。七篇文章的链接如下:
《【AMC12题选】绝对值运算,简单和复杂只有一线之隔》
本文作为这个系列的完结篇,我将对前文中留作思考题的几道题目进行分析点评。按照时间顺序,首先出场的是第二篇文章《【AMC12题选】吓死人的质因数分解》中的思考题:
对所有大于1的整数n,定义pow(n)为能整除n的最大质数的最大的幂。例如,pow(144)=pow(24×32)=32。使2010m整除下面的数的整数m最大是多少?
这道题虽然被排在第25题,但难度确实不算太大,文章的读者留言也已经给出了答案。下面我简略地做一下分析。
由于2010=2×3×5×67,所以我们只需分别确定2, 3, 5, 67在连乘积中出现的次数。
首先计算2出现的次数。根据pow()的定义,如果某个n使得pow(n)的表达式中出现2的幂,则2必须是n的最大的质因数。显然,只有当n是2的幂时才能满足这个条件。
小于5300的最大的2的幂是212=4096,所以连乘积中2的出现次数是1+2+···+12=78。
然后计算3出现的次数。小于5300的数中,形如2m×3的数有11个,形如2m×32的数有10个,形如2m×33的数有8个,形如2m×34的数有7个。与这些数对应的3的出现次数之和为
已经超过了2的出现次数,所以无需继续找下去了。
5的出现次数的计算是完全类似的。形如2p×3q×5的数已经多达41个,即对应的5的出现次数为41次。应该不难推测总的出现次数会大于78。有兴趣的童鞋可以具体算一下具体的数值,这里就不浪费篇幅了。
最后是67的出现次数。形如m×67的数,当m≤67时,67都是最大的质因数。这些数导致的67的出现次数是68次。当m>67时,如果m是质数,67就不是最大的质因数;如果m不是质数,67就是最大的质因数(请注意m的最大值是79)。对于后者,m的取值可以是68, 69, 70, 72, 74, 75, 76, 77, 78,一共9个。所以67的出现次数总共是68+9=77次。
综上所述,67出现的次数最少,是77次,所以m的最大值是77。特别需要注意的是,2的出现次数也仅仅比67多一次。
下一题是第三篇文章《【AMC12题选】多项式,根在哪里?》的思考题:
多项式y=x6-10x5+29x4-4x3+ax2的图像曲线位于直线y=bx+c上方,且只在三个点处与直线触碰。这三个点中最右边的点的横坐标是多少?x6-10x5+29x4-4x3+ax2-(bx+c)≥0对任意实数x成立,且不等式左边的6次多项式恰好有三个不同的实根。
要进一步往下分析,就需要利用多项式的根的性质。由于6次多项式在复数域内应该恰好有6个根(计算重数),所以要么这个多项式有复根,要么这三个实根是重根。在本题中应该是什么样的情况呢?
此时我们就要用到重根的特性。多项式的图像是一条光滑曲线,每一个根都是曲线和x轴的交点。而不同重数的根的“交”法很不一样。
重数为奇数的根(包括单根)的“交”法,是曲线穿过x轴;而重根为偶数的根的“交”法,则是曲线触碰x轴后就往回转。它们的具体形态,我们都可以通过y=xn在x=0处的表现来体会。
把根的这些特性与多项式的值恒非负结合起来看,可以推出三个实根的重数都是偶数,从而都是二重根。于是我们可以把6次多项式写成
x6-10x5+29x4-4x3+ax2-(bx+c)=(x3+px2+qx+r)2.
分别比较等式两边的5次、4次、3次项的系数,可得
2p=-10,
p2+2q=29,
2(r+pq)=-4.
不难解出p=-5, q=2, r=8。要具体求出三个实根的值,就必须对x3-5x2+2x+8进行因式分解。这个过程需要用一点因式分解的经验,最终可得到
x3-5x2+2x+8=(x+1)(x-2)(x-4),
再下一题是第四篇文章《【AMC12题选】把题目读透,解题就完成了一半》的思考题:
设x和y是两个不相等的非零实数,且满足等式
这道题的条件就只有一个等式,不可能把两个未知数x和y的值具体求出来。如果按常规的方程思路去处理,只会把问题变复杂。
第四篇文章的主题是“把题目读透”,具体到这个题目,一方面要注意到题目条件不足以确定x和y的具体值,另一方面题目本身也并不要求x和y本身的值,而是它们的乘积。
看清楚了这两点,就会明白需要考虑另一种处理方法。对于等式条件,有一个常用的技巧是把等号两边的值设为一个待定的量,特别是对于连等式(多于两个表达式的值相等),这个技巧往往能开辟一条有效的路径。
如果记这个待定的量为k,则x应该满足方程x2-kx+2=0。类似地,y应该满足方程y2-ky+2=0。也就是说,x和y都是方程z2-kz+2=0的实根。由韦达定理即可知xy=2。
这道题难度不大,因为这个技巧比较基础,受过一些竞赛训练的学生应该都接触过。所以这道题在AMC12的排序比较靠前,是第8题。但就分析思路而言,它与第四篇文章是切题的。
特别说明一下,x和y的取值是有无穷多种可能性的。同样是根据韦达定理,x+y=k,所以取不同的k值,可对应得到不同的x和y的值,但它们的乘积始终都是2。
最后,如果要用常规的方程处理方法,可以通过因式分解得到(x-y)(1-2/xy)=0,同样可以得到xy=2的结论。
接下来是第五篇文章《【AMC12题选】“时间困难”的问题——起点很近,终点很远》的思考题:
记G为所有具有以下形式的多项式P(z)构成的集合:
其中c1,c2, …, cn-1都是整数。已知P(z)的根各不相同,且所有根都是“整复数”,即形如a+ib的复数,其中a和b都是整数。请问G中一共有多少个元素?这道题只要结合高次代数方程的韦达定理,就不难知道只需寻找绝对值是50的约数的整数根或模的平方是50的约数的整复根。
由于50的正约数有1, 2, 5, 10, 25, 50,所以需要分别对每个正约数列出符合要求的所有根,然后进行组合得到相应的多项式。下面仅对5和10两种情形列出满足要求的根如下:
5:±2±i, ±1±2i, ±5
10:±3±i, ±1±3i, ±10
由于复根必须是成对的共轭复根同时出现,所以第一组根有6种选择方式,第二组跟同样有6种选择方式。把从第一组和第二组选择的根合并起来作为多项式的所有根,即可对应一个多项式。这样一共可以得到36个多项式。
只要把6种情形下的实根和复根都不遗漏地列举出来,并且把它们的组合方式也不遗漏地进行计数,就可以得到答案。然而,要在短时间内精准地完成这两个“不遗漏”的任务,难度其实是相当大的。以我的衡量标准,能在一个小时内得到正确答案的,都可以称为高手!——但每个人只能有一次给答案的机会,也就是只有一次赢得高手称号的机会。欢迎有自信的童鞋尝试挑战一下。
综上所述,这道题确定解题路径很容易,但要毫无差错地走完整条路径却非常困难,此谓文章标题中的“起点很近,终点很远”。
第六篇文章《【AMC12题选】令人心惊的第15题》的思考题我就不分析点评了。在没有时间恐慌的情况下,大家可以慢慢数一下有多少条不同的路径。
最后来看一下第七篇文章《【AMC12题选】绝对值运算,简单和复杂只有一线之隔》的思考题:
定义函数
f(x)=log10(sin(πx)·sin(2πx)·sin(3πx)···sin(8πx)).
f(x)的定义域与区间[0,1]的交集是n个开区间的并集。请问n的值是多少?
真数的表达式是8个正弦函数的乘积,使这个表达式的值大于0的每个开区间的端点处的值都是0。也就是说,每个端点都是某个(或不止一个)正弦函数的零点。
每个正弦函数都会在它的每个零点处变号(从正变负或从负变正)。再看整个乘积表达式(8个函数的乘积),如果其每个零点处都恰好有奇数个正弦函数变号,则从0到1依次经过这些零点,乘积表达式的值就会正负交替,非常有规律。
在这种理想的情形下,我们只需确定乘积表达式的零点的数量,就可以算出n的值。而要找出这些零点并不难,例如,sin(kπx)在(0,1)内有k-1个均匀分布的零点。
然而实际情况并不那么理想。乘积表达式一共有21个零点,其中16个零点处只有一个正弦函数变号,但下面5个零点处有不止一个正弦函数变号:
其中,在1/2处有4个正弦函数同时变号,另外4个零点处都有两个正弦函数同时变号。也就是说,在这5个零点的两侧,表达式的值有可能都为正,也有可能都为负。
我们需要关注的是前一种情形,因为此时这个零点会把原本使表达式的值为正的某个区间切割成两个(使表达式的值为正的)区间,从而使区间的数量增加1。而后一种情形并不会增加区间的数量。
于是,我们首先考虑那16个(只有一个正弦函数变号的)零点,而假设上面的5个零点不存在。此时,使得乘积表达式的值为正的区间有9个。然后,我们再把上面的5个零点一个一个地加进去,看是否会出现把那9个区间切割开的情况。
最终的结果是,有3个零点会切割原有的区间。所以一共有9+3=12个区间组成函数f的定义域。

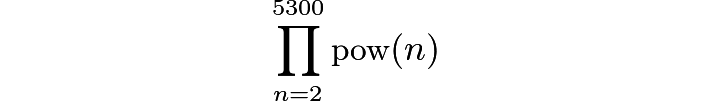
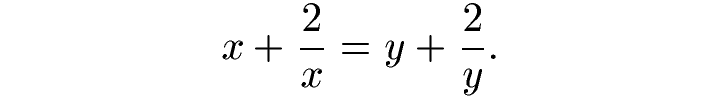
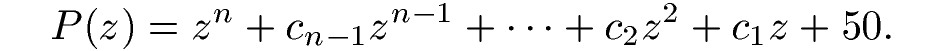



全部 0条评论