1. 甲班和乙班共83人，乙班和丙班共86人，丙班和丁班共88人。问，甲班和丁班共多少人？

解法一：四个班的总人数是：83+88=171；甲班和丁班的总人数=四个班的总人数-乙班和丙班的总人数=171-86=85.

解法二：解法一的思路很巧妙过程很简练，但是很多人苦因没思路最后难以完成。那么我们还有一种虽然复杂，但是却很容易想的方法。设而不求法

像解方程设未知数一样，我们这道题也可以设未知数，只不过这道题并不需要我们解开未知数到底是多少，我们只是借用这个未知数的形式，列式子计算。

设甲班的人数为x，根据甲班和乙班共83人 ，乙班的人数为83-x；根据乙班和丙班共86人，丙班的人数为86-(83-x)=3+x；根据丙班和丁班共88人，所以丁班的人数为88-(3+x)=85-x；甲班和丁班的人数现在都已经知道，那么把他们相加就得到最后的结果了，x+85-x=85.

哎，我们突然发现，我明明设了未知数了，但是最后未知数被消掉了。这就是设而不求法，以设出来的未知数为桥梁，最后找到我们需要的结果，这个方法从小学贯穿到高中，在多个领域都有应用，掌握这种方法能有效帮助我们解决问题。

2. 如图，将0,1,2,3,4,5,6，这7个数填在圆圈和方框内，每个数字恰好出现了一次，组成只有一位数和两位数的整式算式，问：填在方框内的数字是几？

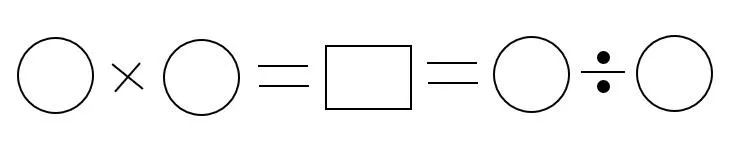
题目说用7个数字组成5个数，说明有3个数是一位数，另外2个是两位数。然后我们大致分析一下这些数的位置。

首先两位数一定不能出现在左边的两个圆圈内。【假设，可以有一个两位数出现在左边的圆圈内，一位数×两位数的结果最少也是两位数，那么方框内一定会是个两位数，而右边的两个数现在只能是一位数，那么一位数之间的除法运算结果绝对不可能是二位数，那么我们最初的假设就是错的。】

其次两位数一定出现在右边的圆圈的被除数位置和方框内。【如果方框内是一位数，那么左边的三个全是一位数，满足题目条件的一位数只有2×3=6，然而剩下的数没办法凑除法了】

然后我们分析0的位置，因为0在乘除法里很特殊，首先0不能出现在一位数的位置，【也就是不能出现在左边的两圆圈和右边的除数圆圈】否则乘法除法的运算结果是0，那么就和题目中每个数字只用一次矛盾了，所以推测0是出现在了两位数的位置，而且只能在个位。继续分析，如果0出现在方框内，那么 ?0= ??÷ ?，倒推出被除数的个位一定是0，与题目条件矛盾，所以，0的位置是被除数的圆圈内。现在我们已经知道了式子大致是 ?× ?= ??= ?0 ÷ ?

同样的道理，1也一样，1出现在了两位数的位置，不过在个位还是十位就要继续分析了。如果1在两位数的个位上，那么 ?1= ?0 ÷ ?，倒推出被除数的个位一定和除数一样，与我们推测出的被除数个位是0矛盾，因此1在两位数的十位上。现在我们已经知道了式子大致是 ?×?= 1?= ?0 ÷ ?

接着我们分析方框中的数具体是多少，方框中的两位数中十位是1，首先0,1都用过了，所以一个一个推测分析。如果是12，发现没问题；如果是13，发现左边两个圆圈乘法凑不成13，不行；如果是14，发现只能是2×7来凑，但是没有数字7，所以不行；如果是15，发现只有3×5来凑，但是数字5已经用过一次了，所以不行；如果是16，发现只能2×8或者4×4来凑，但是都不符合条件，所以不行。最终发现只有12满足要求。

那么左边两个圆圈就能推测出是3×4，那么剩下的数字很明显就能得出 3×4=12= 60÷5.

3. 甲乙丙丁与小强五名同学一起进行象棋比赛，每两个人都要比赛一盘，到目前为止甲一共赛了4盘，乙一共赛了3盘，丙一共赛了2盘，丁一共赛了1盘，问小强赛了几盘？

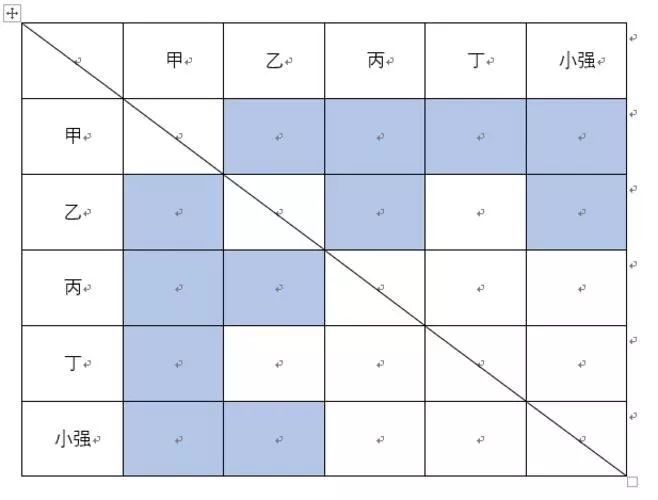
4. 把14拆分成几个自然数的和，在求出这些自然数的乘积，使得得到的乘积尽可能的大，问，这个乘积是几？【较难】