华数之星:牛娃唱着歌做完,普娃打天价酱油(附详细解析)
小高组的真题和解析。

详细解析
第一题
假设两个分子分别为x和y,即x/6+y/337=2021/2022。
因为2022=6×337,两边通分可得:337x+6y=2021
这是个含两个未知数的不定方程,但由于限定了x, y都是整数,所以可以求解(不一定有解,也不一定是唯一解)。
第一种方法是从x=1开始逐个去试(为什么不从y开始呢?因为y的系数6太小了),试验到x=5,可以得出y=56。而x=6时, y=0。因此,只有x=5和y=56一组解。
另一种方法可以用同余。两边同时除以6的余数相等。由于337=6×56+1,因此左边除以6的余数就等于x除以6的余数,用同余式写成:
337x+6y≡x (mod 6)
而2021≡5 (mod 6)
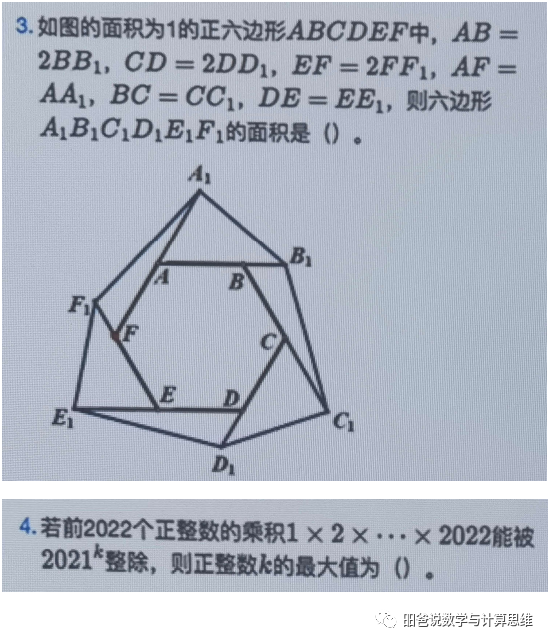
由于0 第二题 不好意思,这题我不会做,感觉题目漏了条件。 第三题 这题就是考察最基本的三角形面积公式。如图,连接A1B, C1D,E1F。假如正六边形的1/6面积为a的话,那外部各个三角形的面积如图,总计是7.5a, 所以,整个面积为2.25。 更多的面积问题可以参考我的文章《万字长文:面积问题怎么求解?》(买过《给孩子的数学解题思维课》一书的就不用付费阅读了,书里有)。 第四题 这题2021换成别的数也一样。没别的,就是要对2021分解质因数。不过,对2021分解质因数还不那么容易。 我们知道,45×45=2025>2021,因此,如果2021是合数的话,那一定有一个小于45的质因数。通过尝试,发现2021=43×47。 下面就看1×2×...×2022能被多少个47整除。由于2022÷47=43...1,因此其中有43个47的倍数,但没有47^2的倍数,因此,k=43。 关于更多质数的话题,可以参考我的文章《孤独而高冷的素数》。 第五题 这题考察整体思维和极限思维。关于这两种及更多的数学思维,可以读我的书《给孩子的数学思维课》。 注意到一场比赛不管胜负情况如何,总是贡献1分(一胜一负和两平都是1分),10个人一共要比赛45场比赛,所有人的分数之和为45分。 由于第一名和第二名都没有输,因此第一名和第二名应该打平。第一名最多得8.5分,第二名最多只能是8分。第三名最多是16.5-10=6.5分。 设S1, S2, ...,S10分别表示第1名到第10名的得分,则有: S1≤8.5, S2≤8,S3≤6.5,S7+S8+S9+S10=S4≤6,S5≤5.5,S6≤5 S1+S2+ ...+S10≤8.5+8+6.5+6×2+5.5+5=45.5 而总分应该是45分,这说明S3只能是6.5分,否则总分就小于45分了。 事实上,据此可以得出前六名的得分分别为:8.5,8,6.5,6,5.5,4.5。 第六题 这题如果不学乘法原理,直接分类枚举找规律也行。 100~199之内: 100,101,102,...,108 110,111,112,...,118 ... 180,181,182,...,188 共计:9×9个 同理,200~299,300~399,...,800~899也各有9×9个 因此,一共有9×9×8=648个。 当然,如果学过乘法原理,那就是百位有1~8这8种填法,十位和个位各有0~8这9种填法,一共有8×9×9=648种。 按照枚举的过程或乘法原理的分析,我们看到: 百位的1~8分别出现了9×9次; 十位的0~8分别出现了8×9次; 个位的0~8分别出现了8×9次; 由于1+2+3+...+8=36,因此总和为: 36×100×9×9+36×10×8×9+36×8×9=320112.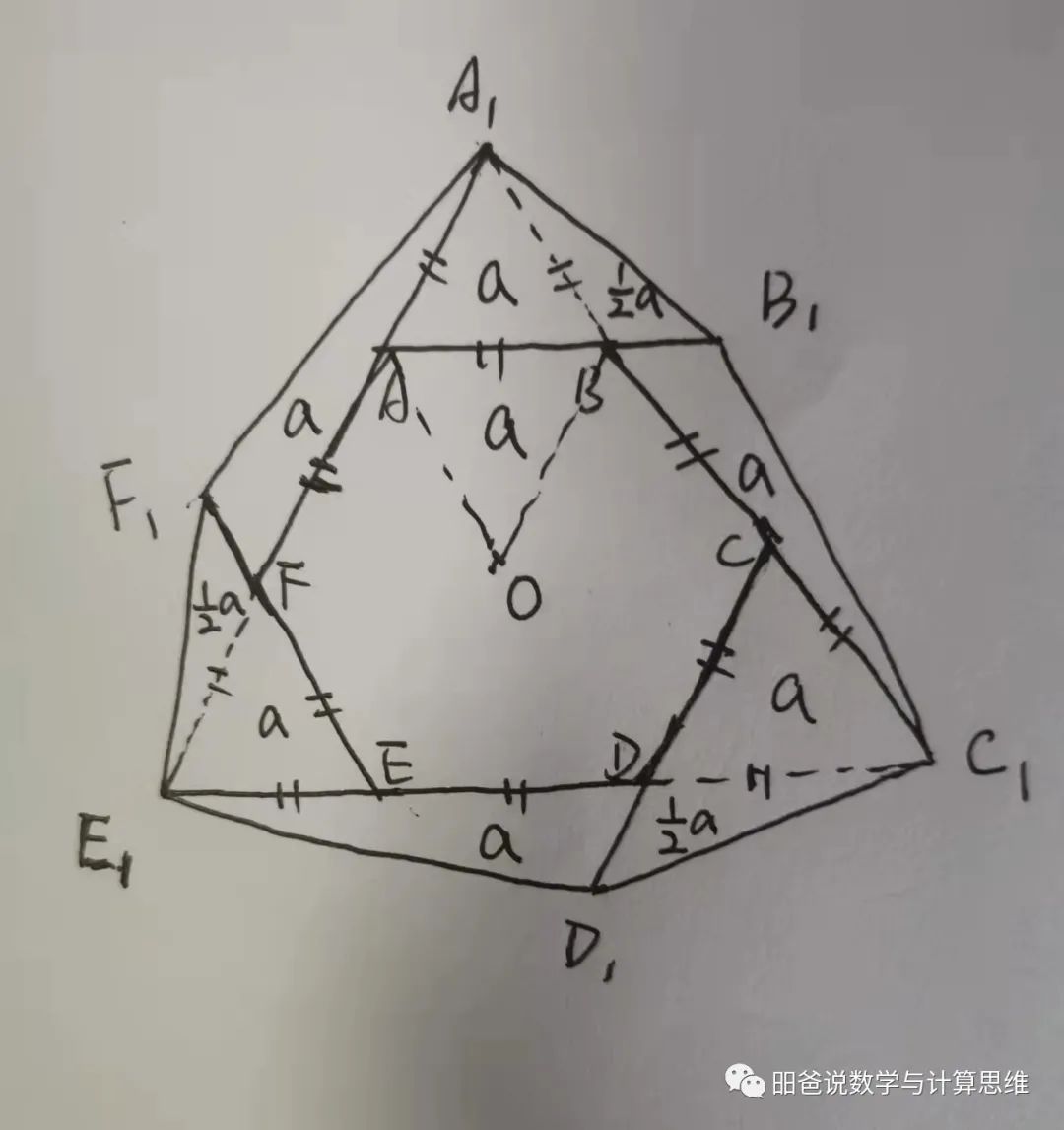





全部 0条评论