第一届华罗庚金杯试题解答和分析(小学册)决赛试题节选
1上期练习答案
1. 53+50-59=44(人),或者 设A班有x人,则B班有53-x人,C班有x-3人,D班有44人。
2. 第二题思路较为复杂,为了方便大家自己梳理,所以原题又重出了一遍。
3.甲比赛4盘,所以每个人都和他比赛过。丁只有1盘比赛,已经和甲比了。乙比赛3盘,因为丁已经比赛完了,那么就和剩下小华、甲、丙比赛。丙2盘,一盘和甲,一盘和乙。所以小华是2盘
4.18=2+2+2+2+2+2+2+2+2,2×2×2×2×2×2×2×2×2=512.又因为18拆出来的2+2+2可以换成3+3,而3×3比2×2×2大,我们尽量把2+2+2全换成3+3,那么18=3+3+3+3+3+3,3×3×3×3×3×3=729。这个乘积是729.
2本期试题讲解

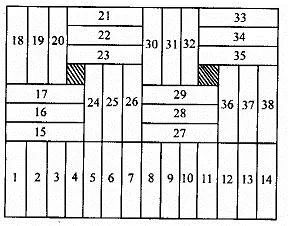
1. 图1是七巧板拼成的正方形,边长是20厘米。问:图中红色部分的面积是多少?
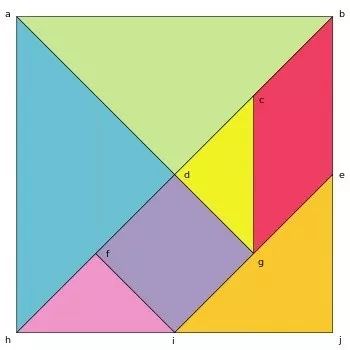
七巧板的这七个部件其实都是由若干个小三角形构成的。我们可以以上图中黄颜色的三角形为标准,将这个七巧板的其余各部分全部分割,就可以看到七巧板的“原貌”了。
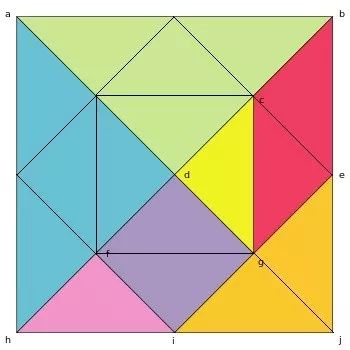
现在我们再来解决这道题就很容易了。正方形的边长是20厘米,所以面积就是20×20=400平方厘米。接下来这个正方形里面有16个大小相等的小三角形,那么每个小三角形的面积就是400÷16=25平方厘米。由于图中的红色部分的面积是两个小三角形构成,所以红色部分的面积就是25×2=50平方厘米。
2. 一个长14厘米、宽11厘米的长方形纸片最多能裁出多少个长为4厘米,宽为1厘米的纸条?怎么裁?请画图说明。
长方形纸片的面积是14×11=154平方厘米,裁出来的纸条面积是4×1=4平方厘米,按照道理来说,154÷4=38.5,也就是说,应该会裁出来38个小纸条然后还剩了一点纸。但是如果我们按照常规思路,从一个角开始慢慢叠放,最终会发现得到这样两种结果。
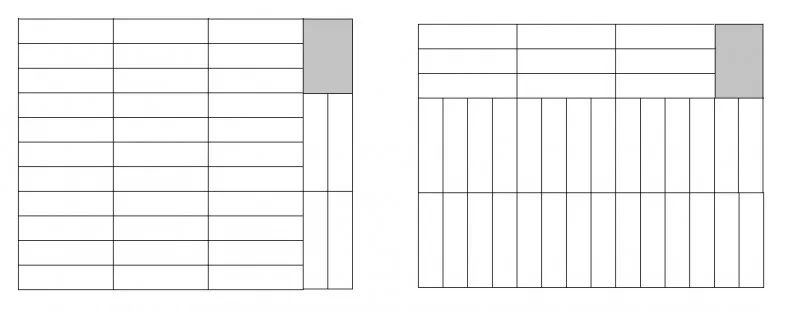
这两幅图的右上角还有6平方厘米的面积没有使用,我们能否找出一种方法把这个6平方厘米中分出来4平方厘米呢?其实弦图可以给我们启示:用3个长方形小纸条可以拼成一个长为4厘米、宽为3厘米的大长方形,4个这样的大长方形就可以拼成一个边长为7厘米的大正方形。【如图所示】
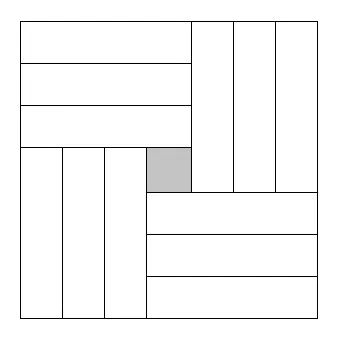
那么我们在设计的时候就可以试着把这样的图形加入到我们的图形中。这样就很容易找到合适的方法了。
3. 有49个小孩,每人胸前都有一个号码,号码从1到49,各不相同。请你挑出若干个小孩,排成一个圆圈,使得任何相邻两个小孩的号码的乘积小于100.你最多能挑出来多少个小孩?
想要挑选的小孩多,那就尽可能挑选号码小的孩子,首先我们把一位数的孩子挑出来,一共九个。
然后我们分析,这些一位数之间相乘肯定不会超过100,那么我们就可以在这些一位数之间插入一些其他的数【其他的数只剩下两位数了】,让这些数之间相乘也不会超过100。在我们挑选的一位数中,最大的是9,我们只要让9和最小两位数10相乘,只要他们的结果确实小于100,那么其余的数字和剩下的两位数相乘,也总有一种不会超过100的组合.也就是说我们可以在9个一位数之间插入9个较小的两位数。
那么现在一共18个数,都是一位数两位数交错排列,也就是说再插入一个两位数,一定会出现两位数×两位数的情况,显而易见,剩余的两位数×两位数>100,所以也就不能再插入新的数字了。那么最多也就挑选出18个孩子。
4. 老师在黑板上写下了13个自然数,让小明计算他们的平均数,小明计算出来的答案是12.43,老师说:只有最后一位数字错了,正确的平均数是多少?
我们分析一下,既然这个数只有最后一位错了,那么这个数最小可能是12.40,最大可能是12.49,那么我们利用平均数倒推回去,计算这13个自然数的总和。
最小是12.40,那么对应的这13个自然数的总和是12.40×13=161.2,最大是12.49,那么对应的这13个自然数的总和是12.49×13=162.37,也就是说,这13个自然数的总和最小可能是161.2,最大可能是162.37。
然而自然数相加的结果一定是自然数,那么我们就在161.2~162.37这个范围内寻找自然数即可。最后发现162这个自然数。那么他就是13个自然数的总和,那么正确的平均数就可以计算出来,162÷13≈12.46。




全部 0条评论