第一部分：试题

2、如果两个质数的和是2019，那么这两个数的乘积是？

3、如果x²=2019x，那么x与901的和是？               .

4、在四位数中，满足各位上数字的乘积等于这四个数字中的某一个，这样的四位数共有多少个？

5、100个小朋友站成一圈，按顺时针方向1〜2报数，凡报“1”的退出。如此一直下去，最后只剩下一个人，这个小朋友最初是第多少号？

6、兄弟两人一起锻炼。弟弟步行锻炼30分钟，哥哥跑步锻炼，跑步速度是弟弟步行速度的5倍，跑的路程是弟弟步行路程的3倍。哥哥跑步锻炼了多少分钟？

7、在镜子中看到钟面（没有标阿拉伯数字那种）上的时间是7：10，实际时间应该是？

8、自然数a和b各自恰好有5个不同的约数，ab有多少个不同的约数？

9、年龄分别为11岁至31岁的21个人围成一个圆圈，将所有相邻两个人的年龄的差值（大数减小数）记录下来，这21个差值总和的最大值是多少？

10、含有相同数字的三位数（如100, 202, 999等都是）共有多少个？

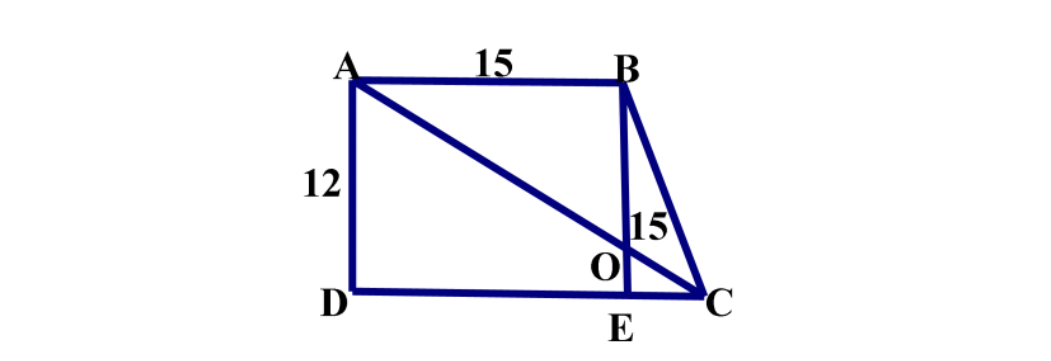
11、计算：4780×99－（476. 4×284＋4764×71. 6） ÷ （1+1/99）

（1）写出这条规律。

（2）运用这条规律计算:

第二部分：解析

2、如果两个质数的和是2019，那么这两个数的乘积是？

质数和是奇数，其中必有一个是2，两数乘积=2×2017=4034。

3、如果x²=2019x，那么x与901的和是？    

解方程得x=2019或0，x与901的和为2920或901。 

4、在四位数中，满足各位上数字的乘积等于这四个数字中的某一个，这样的四位数共有多少个？

（1）有三个数字1：1+8×4=33个。

（2）有至少一个数字0，这里又要再进一步分类：

有1个数字是0：3×9×9×9=2187个。

有2个数字是0：3×9×9=243个。

有3个数字是0：9个。

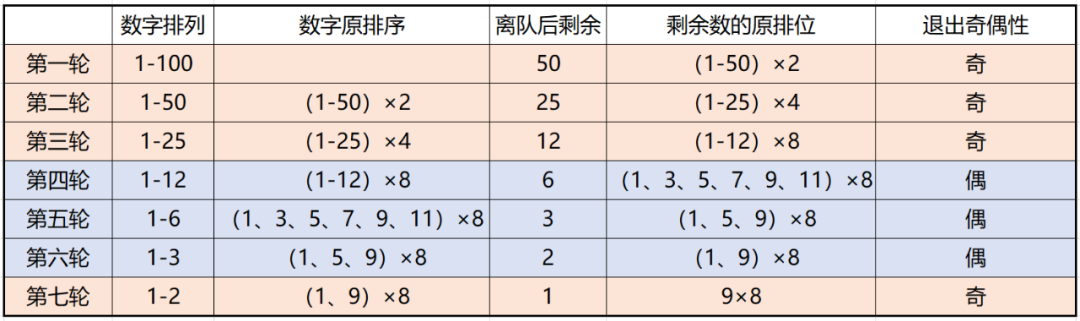
5、100个小朋友站成一圈，按顺时针方向1〜2报数，凡报“1”的退出。如此一直下去，最后只剩下一个人，这个小朋友最初是第多少号？

6、兄弟两人一起锻炼。弟弟步行锻炼30分钟，哥哥跑步锻炼，跑步速度是弟弟步行速度的5倍，跑的路程是弟弟步行路程的3倍。哥哥跑步锻炼了多少分钟？

7、在镜子中看到钟面（没有标阿拉伯数字那种）上的时间是7：10，实际时间应该是？

8、自然数a和b各自恰好有5个不同的约数，ab有多少个不同的约数？

9、年龄分别为11岁至31岁的21个人围成一个圆圈，将所有相邻两个人的年龄的差值（大数减小数）记录下来，这21个差值总和的最大值是多少？

要使年龄差值最大，应该尽量使年龄大的和小的错开排列，如11、31、12、30、13、29、14、28、15、27、16、26、17、25、18、24、19、23、20、22、21。差值总和为20+19+18+…+3+2+1+10=220。

10、含有相同数字的三位数（如100, 202, 999等都是）共有多少个？

11、计算：4780×99－（476. 4×284＋4764×71. 6） ÷ （1+1/99）

答案：1584。

13、一项工程，如果甲先做5天，那么乙接着做20天可完成；如果甲先做20天，那么乙接着做8天可完成。如果甲、乙合作，那么多少天可以完成?

（2）当n=2019时，请你指出覆盖方法。

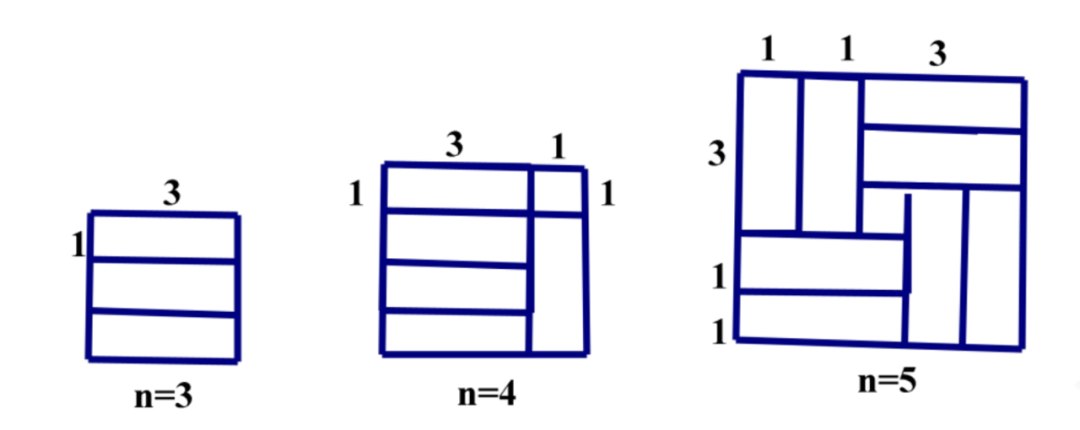
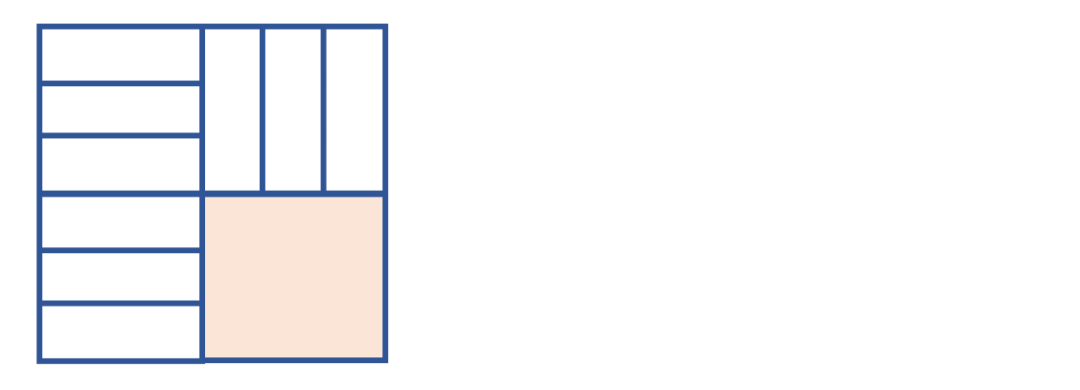
（1）写出这条规律。

（2）运用这条规律计算:

2019²-2018²+2017²-2016²+……+ 3² -2²+ 1

（1）n²-（n-1）²=n+（n-1）。

（2）

2019年五年级一、二、三等奖分数为87分、73分、55分。