2020鹏程杯数学试题及解法(六年级)
【答案】75.
【解析】x × y × z = 2020 - 7 = 2013 = 3 × 11 × 61,所以x + y + z = 3 + 11 + 61 = 75.
- 2 -如图所示,由O点引出的6条射线形成的角满足
∠AOB =∠BOC =∠COD =∠DOE =∠EOF = 18°.
直线l分别交这6条射线依次于点M,G,H,K,L,N.则图中至少有锐角________个.
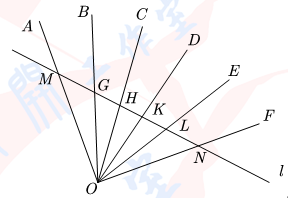
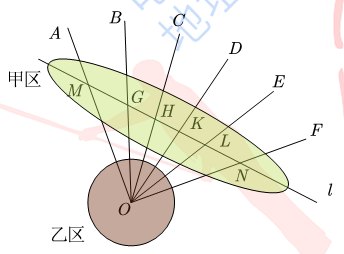
【答案】24.
【解析】甲区有六个交点,每个交点产生4个角,除了互相垂直的情况,都会产生2个锐角;而6组相交,最多只能有一处垂直(若有2处,则加上O点会连接成一个有2个直角的三角形),故至少有5 × 2 = 10个锐角;
乙区6条射线,任意2条可组成1个角,共C(6,2)= 15个角,其中只有∠MON = 18° × 5 = 90°为直角,其余14个角均为锐角.
综述,共有锐角10 + 14 = 24个.
【答案】3.
【解析】考察一共有多少个因子“5”.两位数中含2个因子5的数有25、50、75三个,都含有数字5,故最多只能采用一个,含1个因子5的数则要求个位是5或0.所以乘积中最多有2 + 1 = 3个因子5,即结尾最多只能有3个连续的0.取两位数25和40,其乘积为1000,可满足要求,故答案为3.
- 4 -
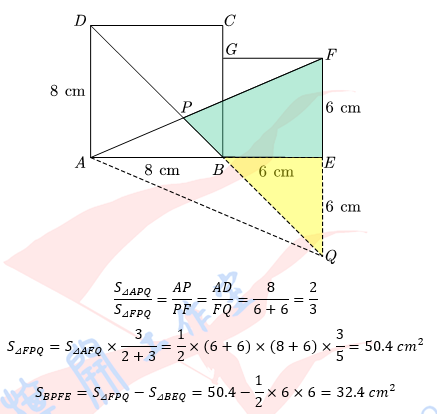
边长分别为8厘米和6厘米的两个正方形ABCD与BEFG如图并排放在一起连接AF交BD于P.则四边形BPFE的面积是________平方厘米.
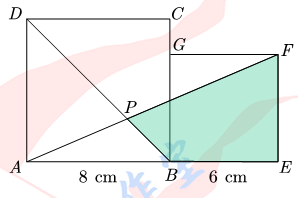
【答案】32.4.
【分析】本题中,把不规则的四边形分成2个三角形进行计算略显复杂,所以我们可以把不规则的四边形补成规则的三角形,用整体减空白进行计算.
【解法一】
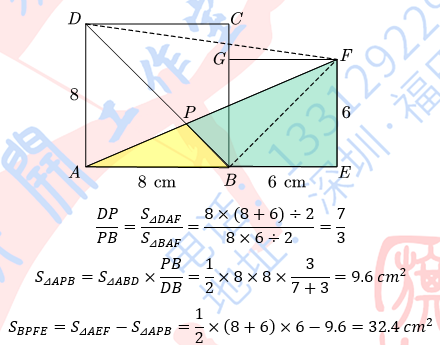
【解法二】
【答案】1023456987.
【解析】使前7位最小,得1023456XXX,末3位的数字为7、8、9,有A(3,3) = 6种排列方式,故第6个数为最大的那个:1023456987.
- 6
-一杯盐水,第一次加入一定量的水后,盐水的浓度变为15%;第二次又加入同样多的水,盐水的浓度变为12%;第三次再加入同样多的水,盐水的浓度将变为________%.
【答案】10.
【解析1】设每次加入的水为1份,
分析第二次加水这个动作,


【答案】71428928571.
【解析】1000000 ÷ 7 = 142857…1,故
S = 7 × 1 + 7 × 2 + … + 7 × 142857
= 7 × ( 1 + 2 + ⋯ + 142857)
= 7 × 142857 × 142858 ÷ 2
= 999999 × 71429
= 71429000000 - 71429
= 71428928571
- 8 -
今年,祖父的年龄是小学生明明年龄的6倍.几年后,祖父的年龄将是明明年龄的5倍.又过几年以后,祖父的年龄又将是明明年龄的4倍.祖父今年是________岁.
【答案】72.
【解析】利用年龄的差不变.祖父的年龄是小学生明明年龄的6倍,意味着年龄差是明明年龄的5倍;即年龄差是5的倍数.同样的理由,年龄差也是4和3的倍数,即年龄差为5、4、3的公倍数,即60的倍数.当年龄差为60岁时,今年明明的年龄是60 ÷ 5 = 12(岁),正是小学生的年龄,爷爷为12 × 6 = 72(岁).若年龄差为120或更大时,明明的年龄与小学生不符.
- 9 -
如图是一个容积为30立方厘米的正方体铁皮盒被剪去一个“角”后的平面展开图(图中相同字母表示长度相等的线段).各侧面剪掉的三个阴影三角形的面积分别为2平方厘米、3平方厘米、3平方厘米,则该铁皮盒最多能装________立方厘米的水.
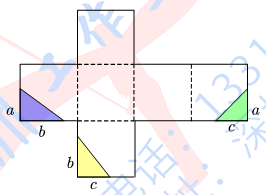
【答案】28.

【答案】20.
【解析】设五年级选手有m人,则比赛场数为

二、解答题(11~15题)
- 11 -

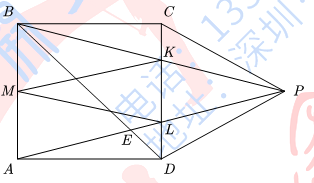
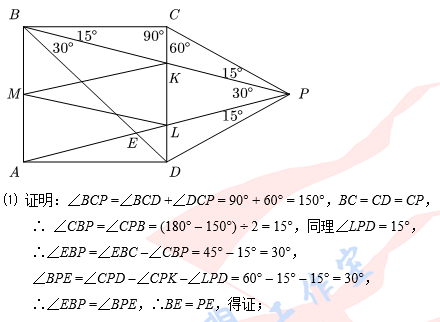
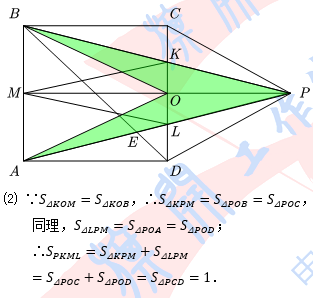
⑴ 证明:BE = PE;
⑵ 求四边形PKML的面积.
⑴ 试举一个鹏程三角形的实例;
⑵ 证明:不存在周长为2020的鹏程三角形;
⑶ 证明:鹏程三角形一定不是直角三角形.
【解析】
⑴ 三边长为3、5、7(开放式答案,满足2条即可:①质数,②较小的2个数之和大于最大的数);
⑵ 若三个质数均为奇数,则其和为奇数+奇数+奇数=奇数≠2020,故3个质数中必须包括一个偶数质数,即2,另外质数为奇数,且不相等,所以它们的差≥2,不满足三角形“两边之差小于第三边”的性质,即不存在周长为2020的鹏程三角形;
⑶ 证明:假设存在鹏程三角形是直角三角形,三边长a,b,c为3个质数,并满足a² + b² = c²;因为奇数+奇数≠奇数,a²,b²,c²中必须有一个是偶数,即必须有一条边的长度为2,此时另外2条边的长度为不相等的奇数质数,其差≥2,不能与边长2组成三角形,矛盾,
故假设不成立,鹏程三角形一定不是直角三角形.
- 15 -
在一块平地上站着n个人,对每个人来说,他到其他人的距离均不相同,当有火灾信号发出时,每人都用水枪击中距他最近的人。
⑴ 当n = 2020时,请你举例说明,可能每个人身上都是湿的;
⑵ 当n = 2021时,证明至少有一个人身上是干的.
【解析】
⑴ n为偶数,可以两两近距离配对,分成1010组互相射击,可以使每个人身上都是湿的.
⑵ 证明一:
① 每人都用水枪击中距他最近的人,所有这些“最近的距离”一定存在最大值,不妨设A击中B的距离是最大的.
② 若B击中其他人,则无人射向A,则A身上是干的.
若B也击中A,则称AB配对,去掉A、B,在剩下的人中重复第①步.
每次操作,要么发现了保持干的人,要么成对地去掉2人.
因为n是奇数,所以不可能通过去除2人全部去掉,所以必然至少有1个人是干的.
证明二:
① 两两之间的距离中,一定存在着最小值,不妨设A和B的距离是最近的,显然A击中B,B击中A.
② 若剩余的人中,有人击中A或B,则导致A或B被击中了2次,则一定有人没有被集中,是干的.
若剩余的人都没有击中A或B,则去掉A、B,在剩下的人中重复第①步.
每次操作,要么证明一定有保持干的人,要么成对地去掉2人.
因为n是奇数,所以不可能通过去除2人全部去掉,所以必然至少有1个人是干的.




全部 0条评论