第一部分：试题

1、字谜ab＋cd＋ef＋gh =128，其中不同的英文字母表示不同的非0数字，则（a＋c＋e＋g）×(b＋d＋f＋h)的值是？

2、x台拖拉机，每天工作x小时，x天耕地x亩，则y台拖拉机，每天工作y小时，y天耕地多少亩？

3、时钟在6:25这个时刻，分针与时针的夹角是？

4、不能写成3个不相等的合数之和的最大奇数是？

5、如图所示，在边长为12厘米的正方形ABCD中，分别以BC、CD为直径在正方形内画两个半圈，这两个半圆的交点为O，则图中阴影部分的面积是多少平方厘米？

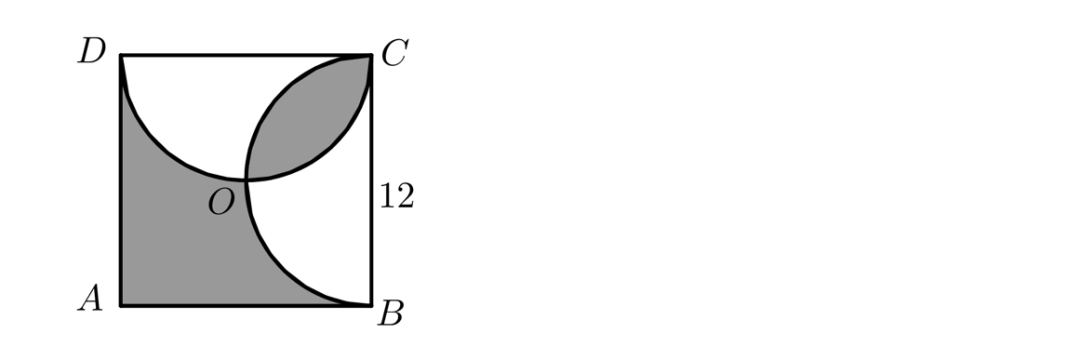
6、老师派若干名学生去购买单价为3元或5元的贺年卡，规定每人至少买一张贺年卡，且每人购买两种贺年卡的总金额不超过15元；如果要求至少有3名学生购买的两种贺年卡的数量完全相同，那么最少要派多少名学生去购买贺年卡？

7、王明参加了10场数学擂台赛，他输的场数、打平的场数都大于他赢的场数，则王明最多赢了多少场比赛？

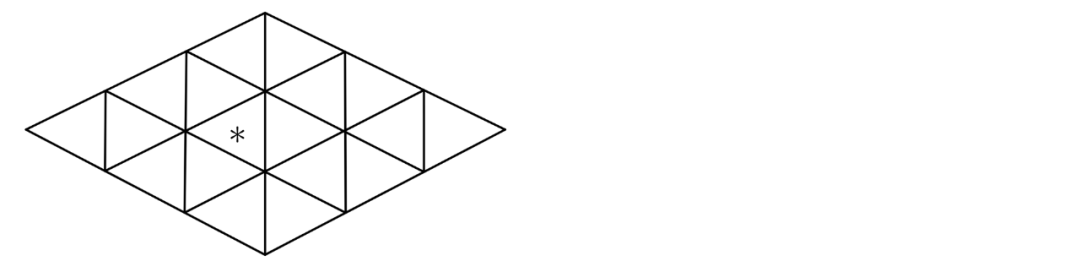
8、如图，有一个由18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形，图中包含“*”的各种大小的正三角形一共有多少个？

9、有浓度为30%的溶液若干，加了一定数量的水后稀释成浓度为24%的溶液，如果再加入同样多的水，溶液的浓度为？

10、在长为1、2、3、4、……、199、200的这200条线段中，选取k（≥3）条，使得这k条线段中任意3条为边都可以构成三角形，则k的最大值是？

11、已知{23.25×[40/31×（△-1）-△]+1/4×△ }÷4/3=1，求出算式中的△。

12、用橡皮泥做一个棱长为4cm的正方体。

(1) 如图，在顶面中心位置处从上到下打一个边长为1cm的正方形通孔，求打孔后的橡皮泥块的表面积。

(2) 如果在第（1）题所述橡皮泥打孔后，又在正面中心位置从前到后再打一个边长为1cm的正方形通孔，求两次打孔后的橡皮泥块的表面积。

(3) 如果在第（1）题所述橡皮泥打孔后，又在正面中心位置处从前到后再打一个长为xcm，宽为1cm的长方形通孔，能不能使所得到的橡皮泥的表面积为130cm²？如果能，请求出x；如果不能，请说明理由。

14、对于正整数n，如果各位上的数字和是一个多位数（含两位数），那么我们再算这个多位数的各位上的数字和，直至得到一个一位数为止，我们将这个一位数记作S（n），例如2018，因2+0+1+8=11,1+1=2，所以S（2018）=2。

大家注意，35×29=1015，根据以上算法，S（35）=8，S（29）=2，S[S（35）×S（29）]=S（8×2）=S（16）=7。有趣的是，S（1015）也等于7。这是巧合还是必然的规律？

15、鹏程幼儿园小张阿姨在“六一”儿童节时给小朋友们发糖果，她将一包糖果放在桌子便回办公室拿东西，回来后发现有些性急的小朋友已各自抓了一把糖果；为了公平起见，她决定通过游戏方式达到平均分配糖果的目的，老师将小朋友们围成一圈，先让所有人数一数自己手中的糖果，凡是奇数的，老师再发一块，然后，每个小朋友将自己糖果的一半分给右边的小朋友；同时，他也收到左边小朋友给的糖果，这样就叫做完成一次“调整”。请你说明：如果张老师手上有足够多的糖果，那么只需要经过有限次“调整”，大家手中的糖果就一样多了！

第二部分：解析

如十位数字和为11，即1、2、3、5，那么个位数字和至少为4+6+7+8=25，不可能为18，不符合题意。

综上，得a＋c＋e＋g=10，b＋d＋f＋h=28，两数相乘结果为280。

3、时钟在6:25这个时刻，分针与时针的夹角是？

分针距离6:30的角度是360/12=30°，时针距离6:30的角度是30×5/12=12.5°，所以，两者夹角为42.5°。

三个数都是奇数时，三个数之和最小为9+15+21=45，

三个数是1奇2偶时，三个数之和最小为9+4+6=19。

即能写出三个不同合数之和的最小奇数是19。可验证：假设比19大的奇数为19+2n，则这个数一定可以写成9+4+（6+2n）的形式。

因此不能写成3个不相等合数之和的最大奇数是17。

5、如图所示，在边长为12厘米的正方形ABCD中，分别以BC、CD为直径在正方形内画两个半圈，这两个半圆的交点为O，则图中阴影部分的面积是多少平方厘米？

连接BO、CO、DO，OC将小叶形分为两个小弓形，分别补在以OB、OD为弦的两个小弓形处，组成直角三角形ABD。因此阴影部分的面积=S△ABD=1/2×12×12=72（平方厘米）。

抽屉原理题，先分析有多少种买贺卡的方式。

合计共有12种买贺卡的方式。要使至少有3名学生购买贺卡方式相同，至少需要12×2+1=25人。

10场比赛，输的和平的都大于赢的场次，说明赢的场次小于1/3。假设赢了3场，这时输的场次和平的场次和为7场，其中必有一个不大于3场，不符合题意。所以，赢的场次最多是2场。

8、如图，有一个由18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形，图中包含“*”的各种大小的正三角形一共有多少个？

如图，共6个。

设溶液有100份，则溶质有100×30%=30份，30÷24%=125，可知加了25份水，再加入25份水后溶液溶质合计有150份。溶度=30÷150=20%。

10、在长为1、2、3、4、……、199、200的这200条线段中，选取k（≥3）条，使得这k条线段中任意3条为边都可以构成三角形，则k的最大值是？

要想构成三角形，即两条较短的边的长度和要大于第三条边，本题中，即选出的数列中，最小的两个数的和要大于最大的数。因为数越大，数之间差的比例越小，所以应从大到小取数。当选取长为100、101、……、199、200的这101条线段，其中任意3条都可以构成三角形，而选取99时，99、100、200不能构成三角形，所以k的最大值为101。

答案：94/21。

12、用橡皮泥做一个棱长为4cm的正方体。

(1) 如图，在顶面中心位置处从上到下打一个边长为1cm的正方形通孔，求打孔后的橡皮泥块的表面积。

(2) 如果在第（1）题所述橡皮泥打孔后，又在正面中心位置从前到后再打一个边长为1cm的正方形通孔，求两次打孔后的橡皮泥块的表面积。

（1）S1=4²×4+（4²-1²）×2+4×1×4=110平方厘米。

（3）分两种情况讨论。

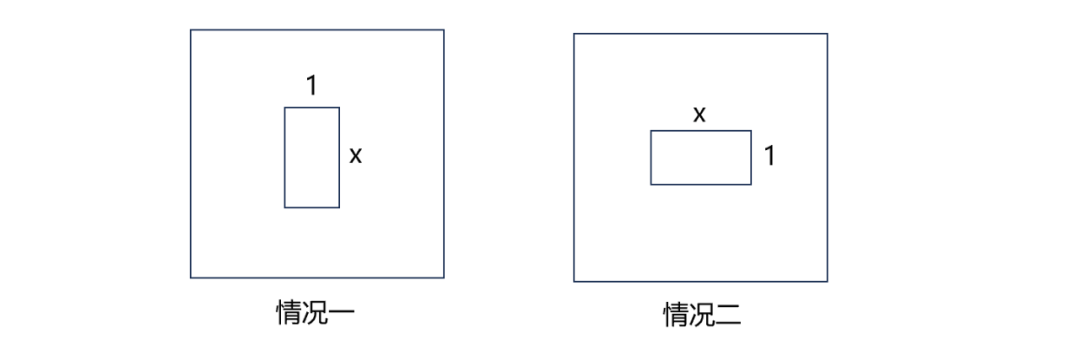
情况一，S=S1-4x+（1.5+1.5x）×4=116+2x=130，解得x=7，不符合题意。

情况二：S=96-2x+（2+2x）×4-4+4×1.5×2=112+6x=130，解得x=3，可以使得橡皮泥表面积为130平方厘米。

13、甲、乙、丙、丁四个人骑着摩托车到外面探险，每辆摩托车带的油最多能行360千米，路上无加油站，为了使其中有人走得更远些，他们想出一个巧妙的方法，且都能安全地返回出发点．那么，他们想出了什么办法使其中有人能行得更远些？最远能行多少千米？

（1）设甲、乙、丙、丁四人同时从A地出发，行了x千米在B地停下，甲给乙、丙、丁各加能行x千米的油，再留足这四辆车返回A地时所需的油；依题意，列方程得：x+3x+4x=360，解得x=45千米，即AB=45千米；

（2）设乙、丙、丁三人同时从B地出发，行了y千米在C地停下，乙给丙、丁各加能行y千米的油，再留足这四辆车返回B地时所需的油；依题意，列方程得：y+2y+3y=360，解得：y=60，即BC=60千米；

（3）设丙、丁两人同时从C地出发，行了z千米，在D地停下，丙给丁加能行z千米的油，再留足这两辆车返回C地时所需的油；依题意，列方程得：z+z+2z=360，解得z=90，即CD=90千米；

（4）丁从D地出发，行至最远处E地，则DE=36÷2=180千米。

综上，最远可以行45+60+90+180=375千米。

14、对于正整数n，如果各位上的数字和是一个多位数（含两位数），那么我们再算这个多位数的各位上的数字和，直至得到一个一位数为止，我们将这个一位数记作S（n），例如2018，因2+0+1+8=11,1+1=2，所以S（2018）=2。

(1)根据以上材料，你能提出一个猜想吗？从等式左边数的个位和数的位数入手考虑，尽量使你的猜想适用范围更广。

(2)请说明你提出猜想的理由。

(3)请举出以上结论的一个应用。

(1)猜想：若m、n为自然数，则S[S（m）×S（n）]=S（mn）。

(2)任意一个自然数和它的各个位置上的数字和被9除所得的余数相同，以四位数为例，因为abcd=1000a+100b+10c+d=9（111a+11b+c）+(a+b+c+d)，所以abcd=a+b+c+d（mod9），即S（x）=x（mod9），从而有S[S（m）×S（n）]=S（m）×S（n）（mod9）=mn（mod9）=S（mn）（mod9）。S[S（m）×S（n）]=S（mn）。

(3)结论可以用于验证两个（或几个）较大的整数相乘的计算结果是否正确；例如：23568×436789=10394243152，因为S（23568）=6，S（436789）=1，S（6×1）=6，而如果S（10394243152）=7，我们可以断定计算有误。

15、鹏程幼儿园小张阿姨在“六一”儿童节时给小朋友们发糖果，她将一包糖果放在桌子便回办公室拿东西，回来后发现有些性急的小朋友已各自抓了一把糖果；为了公平起见，她决定通过游戏方式达到平均分配糖果的目的，老师将小朋友们围成一圈，先让所有人数一数自己手中的糖果，凡是奇数的，老师再发一块，然后，每个小朋友将自己糖果的一半分给右边的小朋友；同时，他也收到左边小朋友给的糖果，这样就叫做完成一次“调整”。请你说明：如果张老师手上有足够多的糖果，那么只需要经过有限次“调整”，大家手中的糖果就一样多了！

在进行调整时，持有糖果最多的要分m块给右边的小朋友，接受左边小朋友的一半（≤m），所以，持有糖果最多的小朋友的糖果会减少或最多持平。同样，持有糖果最少的小朋友的糖果会增加或最多持平。