本文依然来自一名要求匿名的家长。五年级导引是全套导引里面最重要的一本，三导难度不高，四导是过渡，五导是重点，六导是复习。几乎所有小高的重要知识点都涵盖在五导里，没有任何一讲是容易的，没有任何一讲是不重要的。

一道题目可以做很多遍，最重要的就是第一遍。因为经典题目是不可再生资源。所以在讨论具体方法之前，我们先学习一下导引前身《仁华学校数学思维训练导引》的第一作者姚健钢博士的观点。

作者

姚健钢博士是人大附中第一枚IMO金牌（满分），下图是导引中关于他的介绍，是高思学校徐鸣皋校长的学生，在北大学习期间，他在华校讲课并带头编写了《仁华学校数学思维训练导引》，当时只有1200道题目，由于历史原因，难度和现在相比要偏低一些。

高思在这本书的基础上，把梯度设置的更加合理，并分为兴趣篇、拓展篇和超越篇共3008道题目，而且编写了详细的解答，虽然篇幅增了很多，但是根据我的比较，其实基本框架和形式差不多。

我找到早年姚博士接受的一篇专访，虽然时间已经过去10多年，但是现在看来，里面的观点依然十分适用，我觉得只有原作者对于这套书的评价才是最客观的，理解了原作者的意图，然后再去研究这本书才能发挥这本书的价值，以下所有内容均是摘录的重点，大家有兴趣可以搜一下原文。

一、关于刷题

学数学的最好办法是做数学，但切不可陷入极端，为了做题而做题。把孩子做题的数量作为衡量水平的标准是非常错误的。题目是永远做不完的，要引导孩子在解题的过程中从多方面多角度思考，对具有相似性的题目加以比较和归纳，逐渐实现思维能力的提高，养成良好的数学直觉。

一套完整的知识体系是由若干个知识点构成的，好的习题有助于学生将知识体系中各个孤立的知识点相联系并逐渐在头脑中形成一个网络。优秀小学生的直观思维非常强，未必说得出这张知识网络，但是潜意识中有，因而就能在各种竞赛和考试中以不变应万变，比较快地找到解决问题的办法，取得优异成绩。

二、关于难度

可以把难度定在稍微超出孩子现有解题能力一点点的层次上，让孩子不能轻易的得出答案，但是经过老师的引导和自己的思考后又能逐步地解决。这样，孩子每做出一道题不仅提高了自己的数学能力，而且很有成就感，久而久之，学习兴趣和自信心会不断增强。

由于进入重点中学的竞争十分激烈，命题又有很大的随意性，因此某些试题的难度确实很大。我对这种现象很忧虑，例如二年级学生的考试中就出现分数，六年级的试题很多必须用初中代数公式求解。这样做很容易诱导学生去超前学习，而不是把精力放在提高解题能力上。奥数教育强调的是“超常”，而非“超前”。

三、关于题量

《仁华导引》有1200道题，供四个年级用，题目数量确实不多。做完《导引》或者严格说是听老师讲完《导引》并不是一件难事，但是孩子是否真正理解每道题就是另外一码事了。个别水平不高的教师，他讲的问题的解法就不是最优的，没能体现出我希望通过题目所表达的数学思想或技巧。

如果对一道难题的解法，学生只是知其然而不之其所以然，那么考试中碰到类似的题目也不一定能够做得出来。数学的学习重在理解，因此学《导引》不应追求遍数的多少，要运用恰当的方式。

《导引》应该说只是给学生建立了一个学习的标杆或者大纲。我的建议是在做一道导引题之后，根据学生的掌握情况，再做一两道类似的题目加以巩固，这样孩子才有可能对相关的方法和技巧有良好的认识。然后按照这样的模式，一道题一道题的慢慢做，循序渐进的积累，使孩子在数学上越来越“成熟”。

理念

首先讨论一个现象，网上很多人对于导引的难度评价不一致。有的人说导引题目太老，难度已经跟不上了。还有人说做完了导引发现能力没啥提升。北京十大名师之一的老师曾经说过，能把一本导引吃透的孩子，北京一届不超过50人。作为家长，我只是做完了全套导引，应付平时的奥数题目已经游刃有余了，那么为什么会有差别如此之大的说法呢。

其实开头姚博士的文章已经给了答案，好的文章是要定期反复读的，随着阅历的加深每次都有不同的想法，每当做完一本导引我就仔细看一遍。我的做法也是按照他的思路来，中间再及时修正。下面我直接说一下重点：

要高质量和高水平的刷题，看过不等于理解，做完不等于掌握。水一遍不如留着将来做（当然也可能没有将来）。人的思维惯性非常大，特别是错误的惯性，一道有难度的错题一般做3遍才能掌握（不是背答案）。因此，当下决心做完一本书的时候，一定要坚持做完，遇到问题就解决问题，不要自欺欺人地 “做完”，没有决心干脆就别做。

数学上没有哪个结论是证明不出来的，孩子不能理解和证明的结论，是没有意义的结论，也是记不住的结论。每一个高年级的知识点都需要前面的铺垫，每一个高年级的题目都是之前多个知识点的综合。只靠背结论，在低年级内容不多还可以，但到了高年级是绝对背不完的。

当发现一个知识点掌握不好的话，最该做的就是仔细去推导和证明之前的基础知识，而不是找更多同等难度甚至高难度的题目再做。否则就学乱了，简单题出错，中档题不稳，难题不会。这个我在《浅谈低年级和高年级奥数学习方法的区别》里面详细说过。

从知识点上来说，小奥和初中几乎没有关系，但是从思维能力上来说，小奥肯定能够覆盖中考的难度，我研究过本市中考的部分理科试卷，如果孩子小学能够掌握4星难度，那么将来中考时，绝大多数题目都是口算题，我想这也是小奥能起到选拔作用的原因。

路线

难度要适合：简单题直接跳过，过难题目不要硬上。总的原则还是要负重训练。星级至少比目标高1星，比如分班考是3星难度，那么平时最高就要到4星才能保证稳拿3星。这就是降维的优势，我们从不提前校内，就是用小奥的知识体系来学习，没有任何问题。理论上是不存在奥数成绩好但校内不行的。

睿爸观点：

小学数学鸡娃系列中的“先校内，在小奥”其实是对相对普的娃的建议，我看到的绝大多数在学创+班级的娃提前校内不是必须的。

家长要提前准备：比如做完一道题目以后，能不能现场再编一道类似题目，或者准备一道看起来类似但其实不一样的题目。如果自身能力不够也没关系，可以找找其他练习册提前准备，毕竟常见的经典题型就那么多。就像姚博士在前面说的：“在做一道导引题之后，根据学生的掌握情况，再做一两道类似的题目加以巩固，这样孩子才有可能对相关的方法和技巧有良好的认识。”

如下图，每个题目增加一些相同方法的难度稍微更高一些的题目。或者是适应性更强的题目，比如原题是长方形，那么思考在平行四边形甚至任意四边形是否也适用。一个关键点在角上适用，那么这个点放在边上，图形的内部甚至图形外部是否结论依然成立，这样孩子在学习了一个新的方法以后，可以检验到底有没有吃透，也可以拓展思维。

我做完整的一讲导引需要一个小时左右，但是要准备给孩子讲题至少要再花一个小时，这一个小时我要思考孩子会掉那些坑，如何帮她爬起来。如果我对答案或者自己的做法不满意，我会再去找其他的资料，比如《明心资优》、《奥数教练员手册》，或是各位老师的课程，老师的清单详见《双减时代家长自鸡奥数心得》

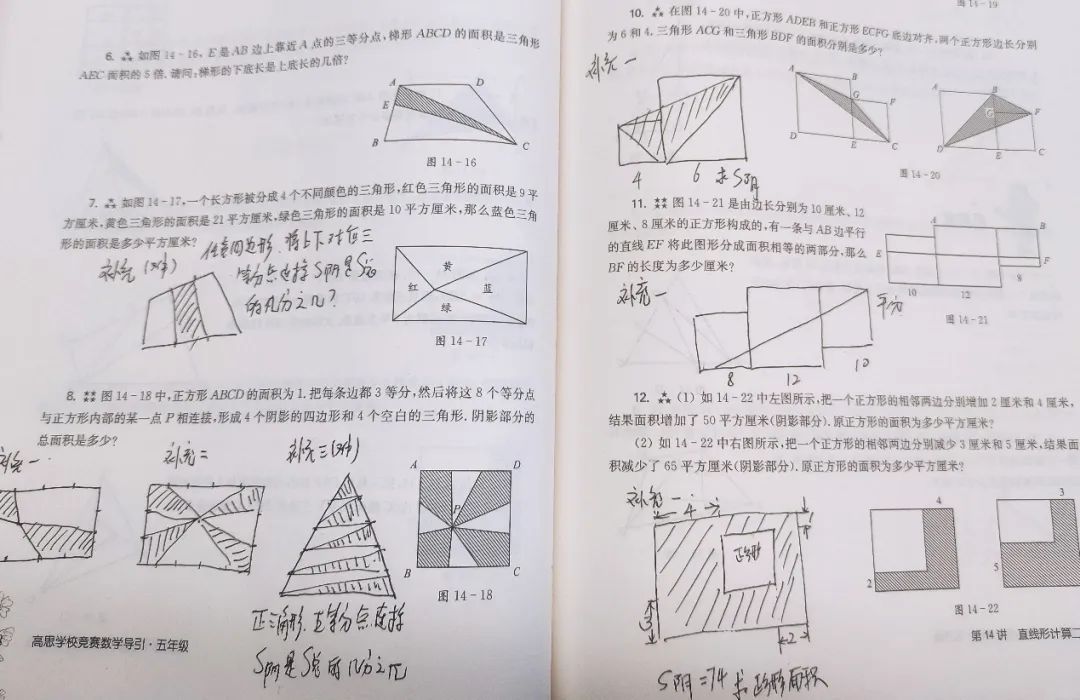
多给孩子一些留白思考的时间，把做题变成讨论题。到了高年级，除了我在《浅谈低年级和高年级奥数学习方法的区别》中提到的以外，还有一个区别在于听课和做题的时间比例问题，低年级如果跟一个机构，上课加上作业每周不会超过5小时，那为什么很多高年级的孩子每周学习小奥要超过10个小时呢？除了多奥的因素外，主要时间都用在了做题和思考上，孩子之间的差距也就在这里。

睿爸观点：

我个人建议上课和做题时间比是1:2，至少是1:1，年级越高，孩子自己在做题中的思考总结更重要。

一题多解，多解归一。即使是导引上简单的题目，也可以深入研究，就是简单问题复杂化。五导的答案基本只有一种解法，但是每当做完了一道题目，家长可以分析有没有其他的解法，和孩子在不断的总结中共同进步，下面我举一个例子。

这是第14讲《直线型计算二》兴趣篇的第8题，这是一道难度不大的2星题，解析通过直接求边上三个三角形的面积间接求出，相当于是利用了面积公式，除了这种方法我又用一半模型、等积变形和比例三种方法分别解答。

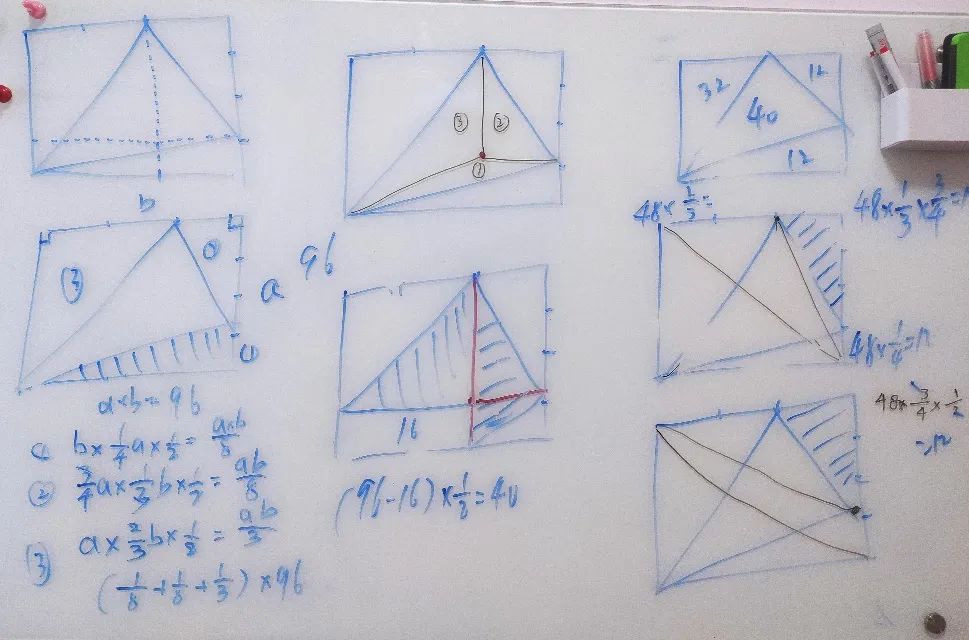
遇到难题多坚持一下。做难题过程中，思维的锻炼和成绩提升是显性福利，坚忍不拔品质的提升是隐性福利，孩子的学习能力和他面对难题时坚持的有效时间成正比。如果你家孩子遇到4、5星题目的时候，就算做不出来，只要孩子还在思考，除非是时间太长了，否则不要轻易打断。

最后也是最重要的，学习尽量少走弯路，但是没有捷径。课是必须学的，题是必须做的。有很多家长会纠结选那个老师的课，刷那本练习册，但没有那个老师的课是完美的，没有那本练习册是最好的。无论是孩子还是家长，每天一道一道题目做下去就行了。

模块

关于各模块的特点我在《浅谈低年级和高年级奥数学习方法的区别》说的已经比较详细了，但是我当时忘说了一个问题，就是各模块的学习顺序，某些模块确实有先后，接下来我会按照做题顺序展开，并说明理由。

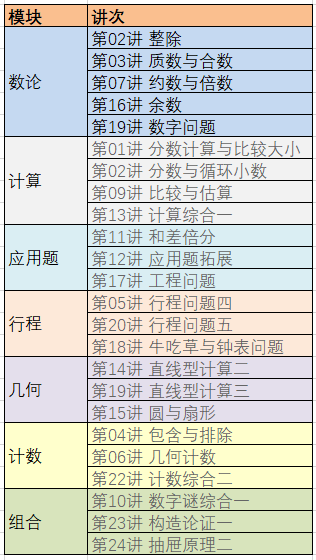
数论：其实机构一般四下就引入，最先学的原因是数论的知识点是通用的，学完以后再看很多问题会有不一样的想法。小奥的数论很难，但是五导除了第19讲以外，其他数论模块的题目都不太难，整除、因倍质合、余数、位值原理这些知识点都是相通的，学了一个知识点，会对其他的知识点有更深的理解。

如果对于深度有一定要求，那么五导的数论无论从数量还是难度都不够，可以继续做六导的数论综合一、二、三，或者四、五年级大白本对应的内容，五导的数论只是一个起点。

计算：五年级计算引入了分数的计算，分数学习需要先掌握数论的知识。刚开始分数的计算会有一些不适应，平时每天要多加练习，如果分数计算基本功没有打好，后面的应用题、行程、几何都要受影响。估算的部分相对较难，因为以前的都是等式，如何进行缩放会是一个难点。

睿爸观点：

不等式的缩放在竞赛中一直是乐此不疲的考点。数学小组的娃在打卡不等式的应用时均分明显下降，我觉得是小学娃相对习惯等式思维，但并不习惯用不等式考虑问题，所以找不等式关系困难，经常忽略对边界的判断，不熟悉不等式缩放的一些常见技巧（首尾相加、分段放缩等）。

应用题：五导最大的变化就是引入了分数和比例，所以要有过硬的计算基本功。算术方法简洁，一般从找不变量和公共量入手，或者列方程解决。这三讲其实没有什么区别，都是同一个问题，工程问题和行程问题的思维方式其实更加类似。这部分到了高年级既不是重点也不是难点，无论用什么方法，能做出来就是好方法。

睿爸观点：

对于高年级小奥来说，应用题即不是重点也不是难点，大多数只是考试时的送分题。但对于高年级校内来说，这部分即是重点也是难点。

行程：行程是高难度应用题，导引里面的行程都不简单，题干文字多，过程复杂，四、五导的行程都是难度最高的章节之一。《行程问题四》是流水行程和环形路线，和四导的火车过桥是同一难度。《牛吃草和钟表问题》里面，牛吃草是四年级课本的内容，所以难度不大。钟表问题也是行程中的相遇和追及。

《行程问题五》是变速问题，这是一个难点，处理变速问题除了通过“同时同线，专人专线”比较外，主要是引入了假设法这个新知识点，另外还要依靠比例和方程这两个利器。难题做不出来非常正常，有的题型见识一下就可以了。

睿爸观点：

就我自刷导引的经历，五导行程问题里面的三星题都很费力。

几何：《直线型计算二、三》主要就是研究比例，经过计算、应用题和行程对于比例的锻炼后，就没有计算上的压力。几何的学习方法是把基本功打好，通过中档题目的练习吃透知识点。图形再复杂，也是由线段和角度组成的，如何能找到其中的联系需要训练，几何不是通过难题练出来的，而是中档题目练出来的。

很多人说辅助线难做。辅助线也不是凭感觉画的，而是需要一定在那里或者将图形旋转过去。没有原因的辅助线就是瞎画，熟悉了之后自然就有做题的感觉。

几何模型很多，本质上就是共边和共角。不需要记结论，而是要记住证明过程，第一反应是找比例，而不是想是哪个模型，什么鸟头、风筝、燕尾、飞镖、双峰、金字塔、沙漏这些，就是为了让孩子容易记住起的名字，仅此而已。水平不行的才会讲模型，应该讲共性，而不是特性。

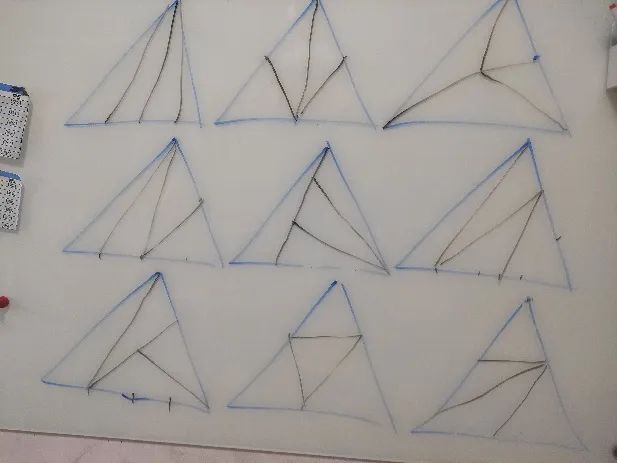
要想几何掌握的好，必须要多画图，在画图中找规律，然后再讲解知识点固化。比如讲直线型计算的比例，不用上来就讲，而是指定一个三角形，让孩子想各种办法4等分，这个操作的过程，就是孩子运用知识点的过程，这个才能记得牢，你多花的这个时间，等后面学习知识点会节省回来，等做到导引类似下图这种题基本就是直接做，因为这个图之前做出来过。

计数：计数和组合放在最后主要是难度的考虑。《包含与排除》就是容斥原理，这个模块的题型较为固定，不会有太大的变化。之前的计数讲究的是不重不漏，实际做题很难满足，那么容斥原理研究的是如何处理重和漏，需要有较好的和差倍和数阵图基础。

《几何计数》这一讲的难度不高，但和所有的计数题目一样，极其容易做错，考试很难全对。枚举对技术要求低，但是非常容易漏，排列组合更多是从总体考虑，和枚举相比正确率更低。越高级的方法，对于水平要求越高。如果是重要的比赛，优先枚举，另外枚举也是一种能力。

本来数论和计数就难，《计数综合二》是关于数论、数字谜和计数交叉知识点，肯定能做出来一些，但全部做出来难度还是很大，连我自己做正确率也不高。

睿爸观点：

数论的题目我能做出来的大概率是对的，但计数的题目则完全没信心。在思路、答案和标答都不同的时候更是麻烦，为了知道自己究竟错那里，经常需要用程序辅助验证。

组合：组合基本就是把所有的难题组合到一起。《数字谜综合一》需要结合分数、循环小数、比较与估算、数论的知识点，难度还是不小的。用到的分类讨论特别多，过程极其麻烦，一边做题一边就会发现天赋对于奥数的重要性。

《构造论证一》主要研究两个问题，是否存在和最值问题。前者只需要构造，后者既需要构造，也需要论证。小奥学过的所有方法都可以放进来，最重要的还是数论，需要多做多题，如果一种类型的题目不会，一定要多补充类似的题目。

《抽屉原理二》最难的就是构造抽屉，还是需要数论的知识（任何模块只要和数论结合都很难），关于这方面我建议还是多见见题型，有些经典的抽屉构造方式要记住，不是说硬记，而是尝试构造其他方式再对比，理解为什么这么构造抽屉。

总结

我家孩子一下做完三导，二上四导，现在二下在做五导，这个进度其实不算太慢，但我从来没有因此而得意，因为我自己非常清楚，拓展篇题目虽然掌握了，但是有的章节第一次正确率并不高。很多超越篇题目孩子并没有吃透，只是我给她讲会了，当时能够跟上思路，再遇到还是大概率不会，以后的路还很长。

其实家长亲自教孩子并不是最优的方法，因为在你给孩子讲的时候，你的角色首先是一个家长，其次才是老师，这就注定了你的劣势地位。就像曾经有个家长说过，严于律己，宽以待娃。