广东省仅一人上榜！2022年IMO国家队选拔第一轮集训结束（附本次集训试题）

0 人点赞了该文章 · 84 浏览

2022年奥林匹克数学中国国家集训队第一阶段闭幕式于今天11点在线上举行。第一阶段集训共有60人参加，经过8天4场考试的激烈角逐，共选拔出15人。

在闭幕式上，首先由中国数学会数学竞赛委员会主任彭联刚教授及中国人民大学附属中学高江涛副校长分别进行致辞，最后由第63届中国队领队北京大学国际数学研究中心肖粱教授宣读进入第二阶段集训的名单：

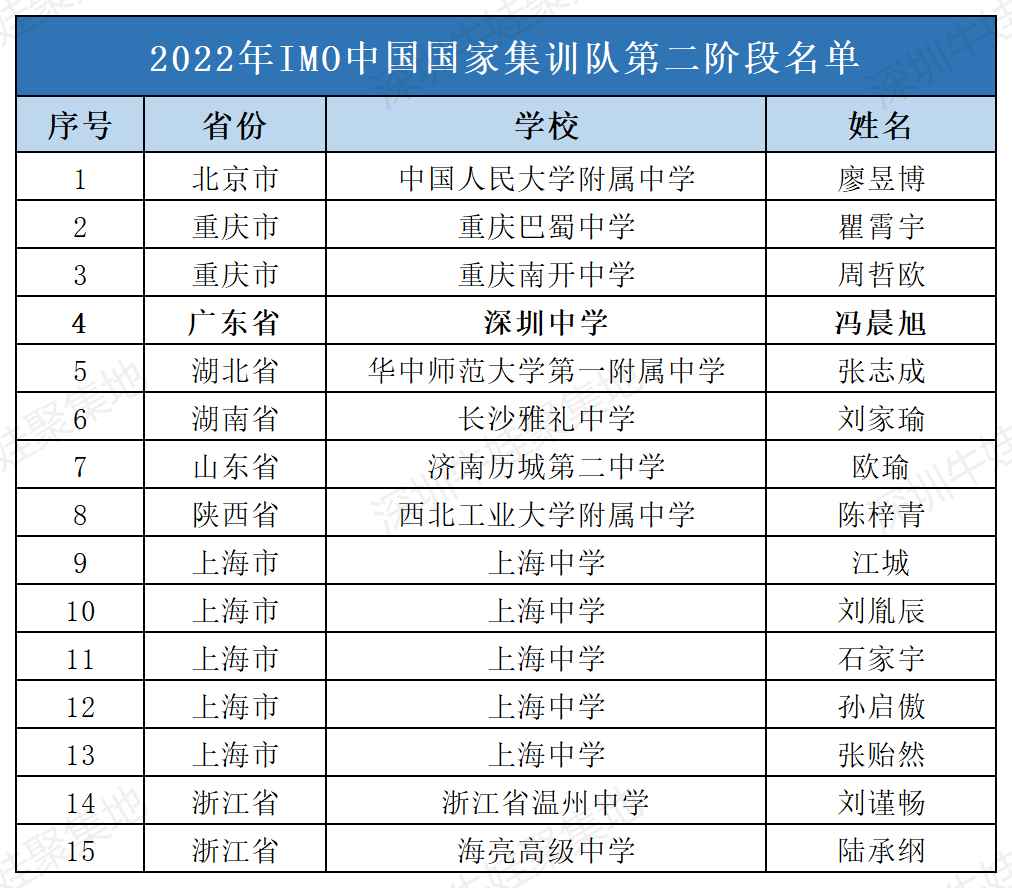
据悉，下一轮集训也将在线上举行，集训结束后将选拔出6名队员进入国家队，代表中国参加今年的国际数学奥林匹克(IMO)。

最后，在这里祝15位同学在下一阶段也能取得令自己满意的成绩！

2022年IMO国家队第一轮集训试题

2022年CTST试题（一）

1.设凸六边形内接于圆，交于点 , 交于点 ,设的外心分别为证明: ,, 交于一点。

2.已知为素数，为无穷整数集，证明：存在的元子集 , 使得中任意个元素的算术平均值不在中。

3.设为给定正整数，且令Q={(x,y,z) ∈ ℤ³ | 0 ≤ x ≤ a,0 ≤ x ≤ a, 0≤ y ≤ b, 0≤ z ≤ c }.

初始时,在中的每个点上放置若干枚棋子(可以不放)，棋子总数为而后可进行如下三类操作：

(1)从点  处拿走  枚棋子，并在点  处放置一枚新棋子.
(2)从点  处拿走  枚棋子，并在点  处放置一枚新棋子.
(3)从点  处拿走  枚棋子，并在点  处放置一枚新棋子.
求  的最小值，使得无论最初的  枚棋子如何放置，都可经过一系列上述操作，使得点处有棋子。

4.在锐角中，内心为为关于边的对称点，延长线交延长线于点作交劣弧于点过作平行线交延长线于点证明：若则

5.设为复平面上的单位圆, 上个(可相同的)复数,,..., 满足中任意一段长度为的开弧上至多有个 ,且任意一段长度为的开弧上至多有个 .求的最大值。

6.设为有限集的个(可相同的)子集，且满足：对有：

证明：可将中元素黑白染色，使得每个的元素既有黑的，又有白的。

注：试题来源于网络

2022年CTST试题（二）

1.求所有正整数对（m,n），在m+1条横线与n+1条竖线构成的方格表中，可以对其中的一些方格添加一条对角线（允许不添加，但不能在一个方格内添加两条对角线）。使得整个图形可以一笔画并回到起点。

2.非直角△ABC满足BC>AC>AB，平面上两个不重合的点P_1、P_2，使得若AP_i、BP_i、CP_i分别与△ABC的外接圆交于D_i,E_i,F_i,则有D_iE_i⊥D_iF_i且D_iE_i=D_iF_i≠0其中i=1,2。

直线P₁P₂与△ABC外接圆交于Q₁，Q₂。Q₁,Q₂关于△ABC的西姆松线交于W。证明：W在△ABC的九点圆上。

3.a₁，a₂，…，a_n为n个两两互相不整除的正整数，即对任意i≠j.

a_i不整除a_j。

证明：a₁+a₂+…+a_n≥1.1n-2n.

注：如果证明了n充分大时的不等式，会适当给分.

4.给定正整数，求的所有最小值点.

5.给定正整数，为的正约数集合，为的映射.证明下面的两个论断等价：
(A)对的任意正约数，有.
(B)对的任意正约数，有.

6.给定正整数、，，、、、，、、、为个实数.证明：使得的正整数对()的对数不超过.

注：试题来源于网络