目录

第6单元

第6单元二元二次式的分解，这个单元介绍了利用双十字相乘法分解二元二次式和三元齐次式。从名字就可以看出，双十字相乘法需要用到大量的十字相乘，所以十字相乘掌握不熟练的同学赶紧回头去看上个单元👉因式分解与技巧0-5单元刷题建议👈（点击蓝字可查看）

通过例1，同学们可以理解如何使用双十字相乘法进行因式分解。

例3是把二元二次式中的双十字相乘法推广到三元齐次式。

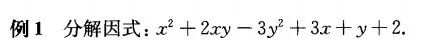
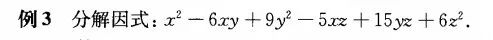
前面的介绍的双十字相乘法都用在6项的多项式中，例5介绍了不足6项的二元二次式和三元齐次式如何处理。

 

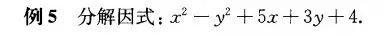
本单元技巧性也很强，第一次接触双十字相乘的同学需要完成习题6进行巩固。练习之后仍不习惯使用双十字相乘法的同学也不用担心，下个单元学习的主元法也可以用来解决本单元的题目。

第7单元

第7单元综合运用，这个单元主要介绍了换元法和主元法两种方法，另外还有一些其他的技巧。

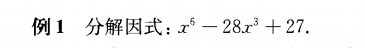
例1可以利用换元法实现降次的目的，把这道题变成大家熟悉的二次三项式，再十字相乘。

例2与例1类似，可以利用局部换元，把这道题变成大家熟悉的二次齐次式，再十字相乘。

 

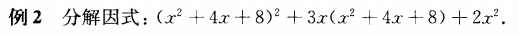
例3与例4虽然看起来完全不同，但是把四个连续整数表示出来之后，例3与例4就变得非常像了，这两道题都是通过分组相乘来构造相同的二次式，再利用局部换元简化题目。

 

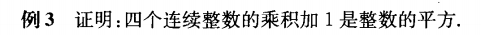
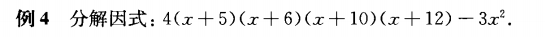
对于以上这些，题目中有重复部分的式子可以利用换元法进行因式分解。

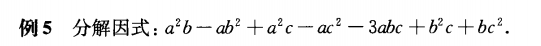
例5是一个含有多个字母的复杂多项式，对于这类式子的因式分解，我们往往使用主元法的技巧，也就是把其中的一个字母作为主要字母，其余字母看做系数。比如，这道题可以把a当做主要字母，于是这个复杂多项式就可以看作关于a的二次三项式，接下来利用十字相乘法进行因式分解。

 

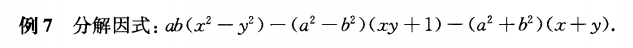
例7和前面题目的不同之处在于这道题可以把a、b都当做主要字母，把这个多项式看作关于a、b的二次齐次式，再利用十字相法乘进行因式分解。

例8展开整理之后是一个三元齐次式，在上个单元中，我们学习过这类式子可以利用双十字相乘法进行因式分解。本单元中，我们学习了主元法之后，就有了另外一种解法。我们以x主要字母，把这个式子看作关于x的二次三项式，再利用十字相乘法进行因式分解。

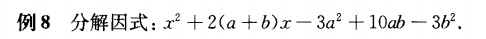
例10有一个新的换元方法，这道题使用均值换元，更便于后续的操作。

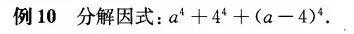
例11的思路是展开之后重新分组。

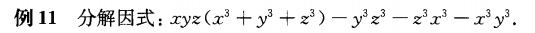
本单元习题7的题目数量较多，而且很多题目与例题相似度很高，同学们可以酌情练习。

以上是6、7单元的内容，这两个单元属于稍微进阶的内容，整体难度适中。这个部分需要同学们掌握拆项、添项、换元法和主元法这些技巧。