No.209 2022年人大附中早培班八上数学期中考试解析
之前只发了试卷,查了一下网上没答案,我就做了一下。23题和25题有点复杂。
1.A 坐标平移变换
2.A 找到135°角即可
3.B 3/4/5的直角三角形
4.C 相似比
5.C 根据交点位置与对称轴位置的关系可判断a<0,k>0
6.A 相似比换算
7.D 对称性;a不能确定,所以AB无法确定正误
8.D 求出k=3/4即可
9.ABC ∠ADC=60°
10.AC y=x²-2x-3
11.ABC 旋转
12.ACD B选项中必须先进行操作三;CD选项由操作次数的奇偶性判断
13.-2 分子分母同除以b
14.-√3≤b≤√3,两条切线的截距为边界
15.1/9 相似比
16.a≥-1 a在对称轴右侧
17.7 DE=CP/2
18.3√2/7

19.同弧所对的圆周角是圆心角的一半;等边对等角
20.(1)y=-(x-6)²/36+3;(2)不会出界
21.(1)
(2)3;3
(3)略
22.(1)连接OC、BD,易证
(2)13/3 连接AC,易证△CDE∽△ABC∽△ACE
23.(1)交点(0,-3);对称轴x=-a
(2)①-4≤y1≤5;y2=-3
②a≥3/2。分类讨论,a>0时,x1离对称轴的距离≥x2离对称轴的距离,解得,a≥3/2;a<0时,x1离对称轴的距离≤x2离对称轴的距离,无解。
24.(1)略,易证全等
(2)若AB`与圆相切,则切线长等于AD=1,切点必然与B`重合,得证。
(3)5/4
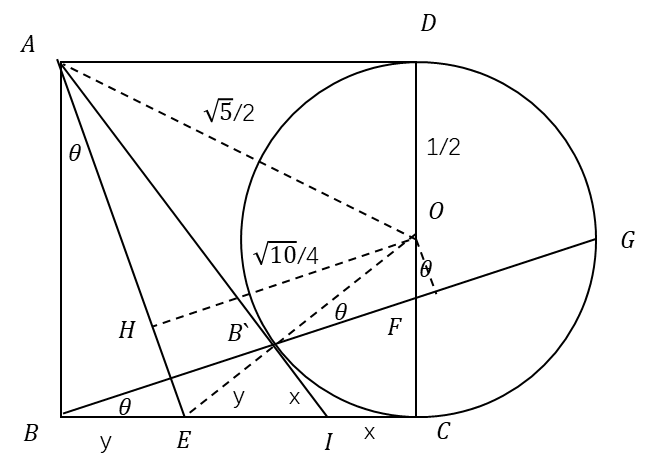
如图所示,易知E、B`、O三点共线。
设BI=IC=x(切线长相等),由勾股定理得
设BE=EB`=y,作OH⊥AE,由等面积法得

算出θ的各三角函数值

则
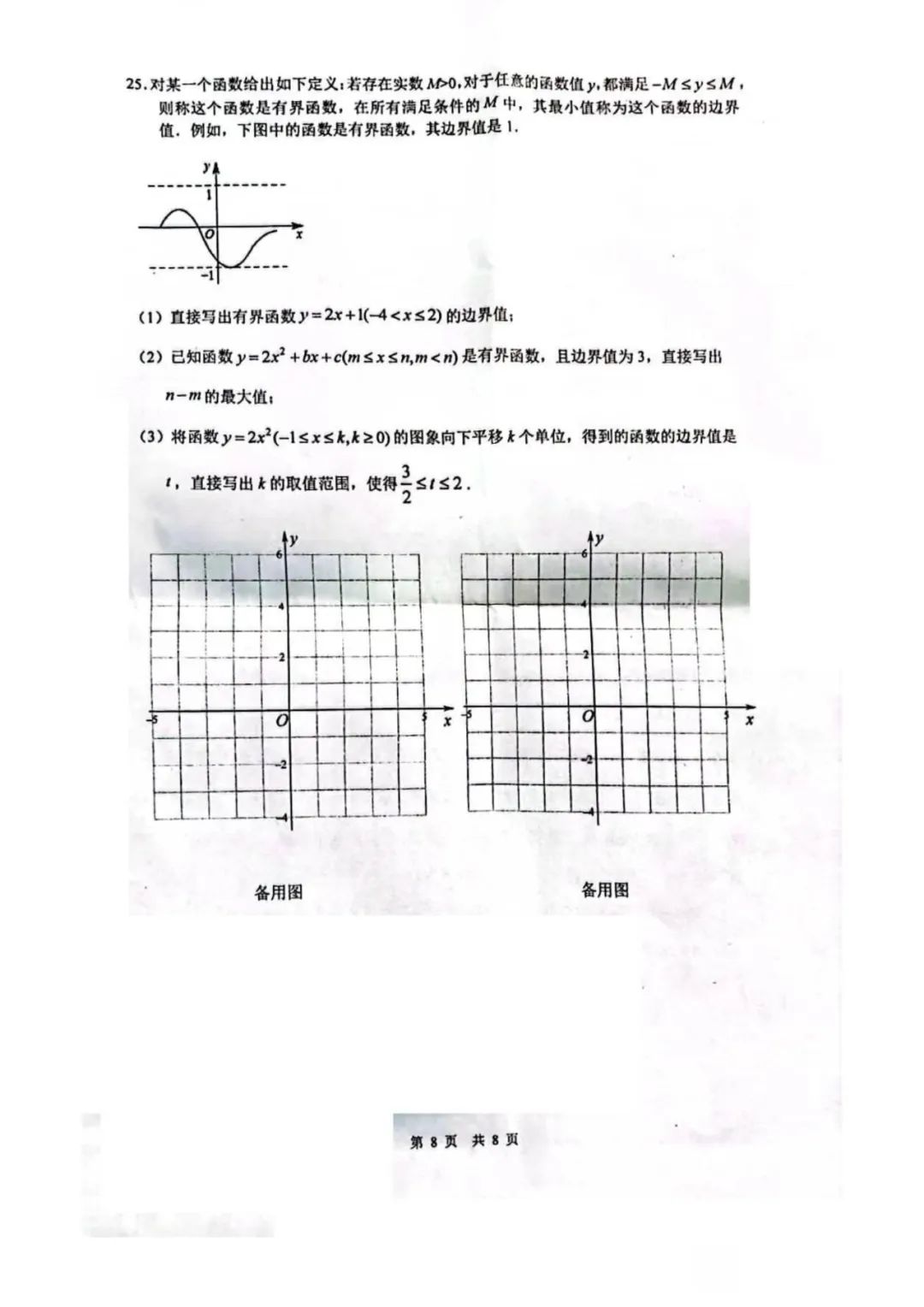
25.(1)7
(2)分类讨论
由题意,顶点纵坐标(8c-b²)/8<3,即b²-8c+24>0。
存在下图两种情形

若-3<(8c-b²)/8<3,则二次函数与y=3的两个交点横坐标之差为n-m的最大值。
由2x²+bx+c=3,得m+n=-b/2,mn=(c-3)/2,则
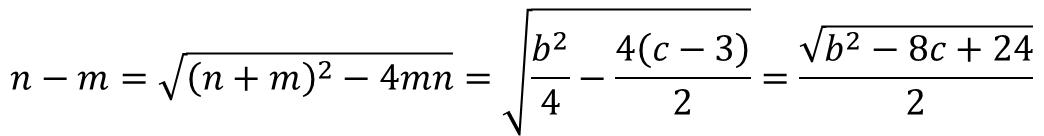
若(8c-b²)/8<-3,m,n只能在对称轴同侧,分别与y=±3的交点的横坐标之差为n-m的最大值。不妨取m,n同在对称轴右侧,则
2n²+bn+c-3=0;2m²+bm+c+3=0
求根公式求出两根,再作差

(3)0≤k≤1/2或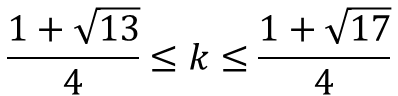
由题意,首先必须满足k≤2
平移后函数解析式为f(x)=2x²-k,则
f(-1)=2-k,f(0)=-k(函数最小值),f(k)=2k²-k
根据条件3/2≤t≤2,分类讨论:
①若0<k<1,则f(-1)>f(k),此时函数最大值为f(-1)=2-k。因为此时|f(0)|=|-k|<1,所以必须满足3/2≤f(-1)=2-k≤2,解得0≤k≤1/2。
②若1≤k≤2,则f(-1)>f(k),此时函数最大值为f(k)=2k²-k。
a)若1≤k<3/2,则需满足3/2≤f(k)=2k²-k≤2,解得
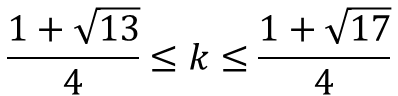
b)若3/2≤k≤2,则需满足f(k)=2k²-k≤2,此时无解。
综上,0≤k≤1/2或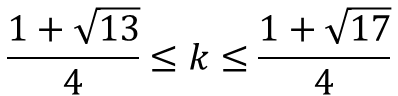
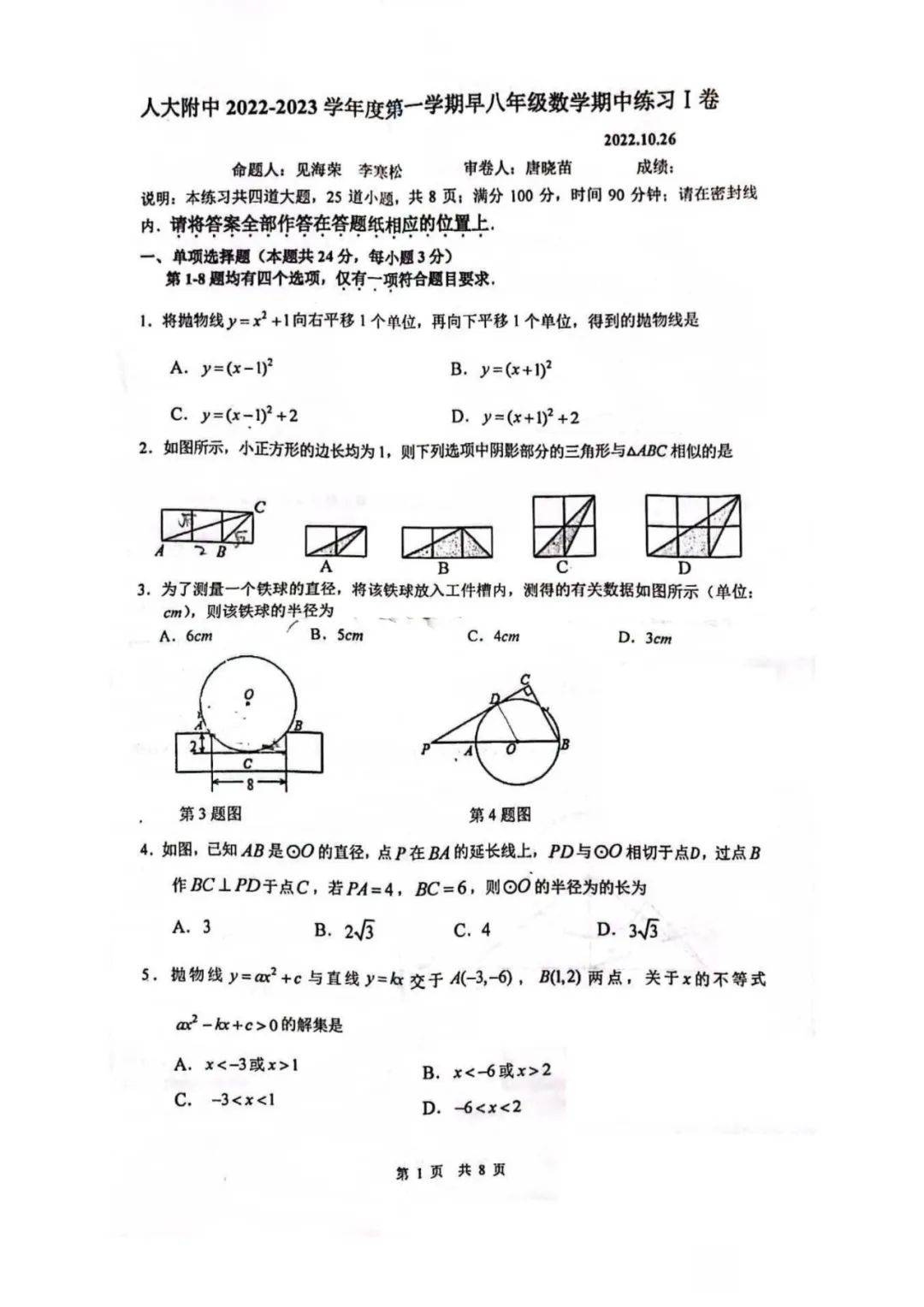
附试卷:











全部 0条评论