2022年六年级希望杯100题解析
希望杯最好的复习材料莫过于官方出品的《希望杯100题》了,每年活动前都会发布,和正式活动的知识点吻合度非常高,基本上可以认为是考试大纲。所以在准备希望杯的过程中,这100题是必刷的。
但是官方只给出了100题的答案,但是并没有给出解析,下面给大家分享一下解析的手写版。在解析之后也会有对整个知识点分布的梳理。
《希望杯100题》解析
01-48题解析


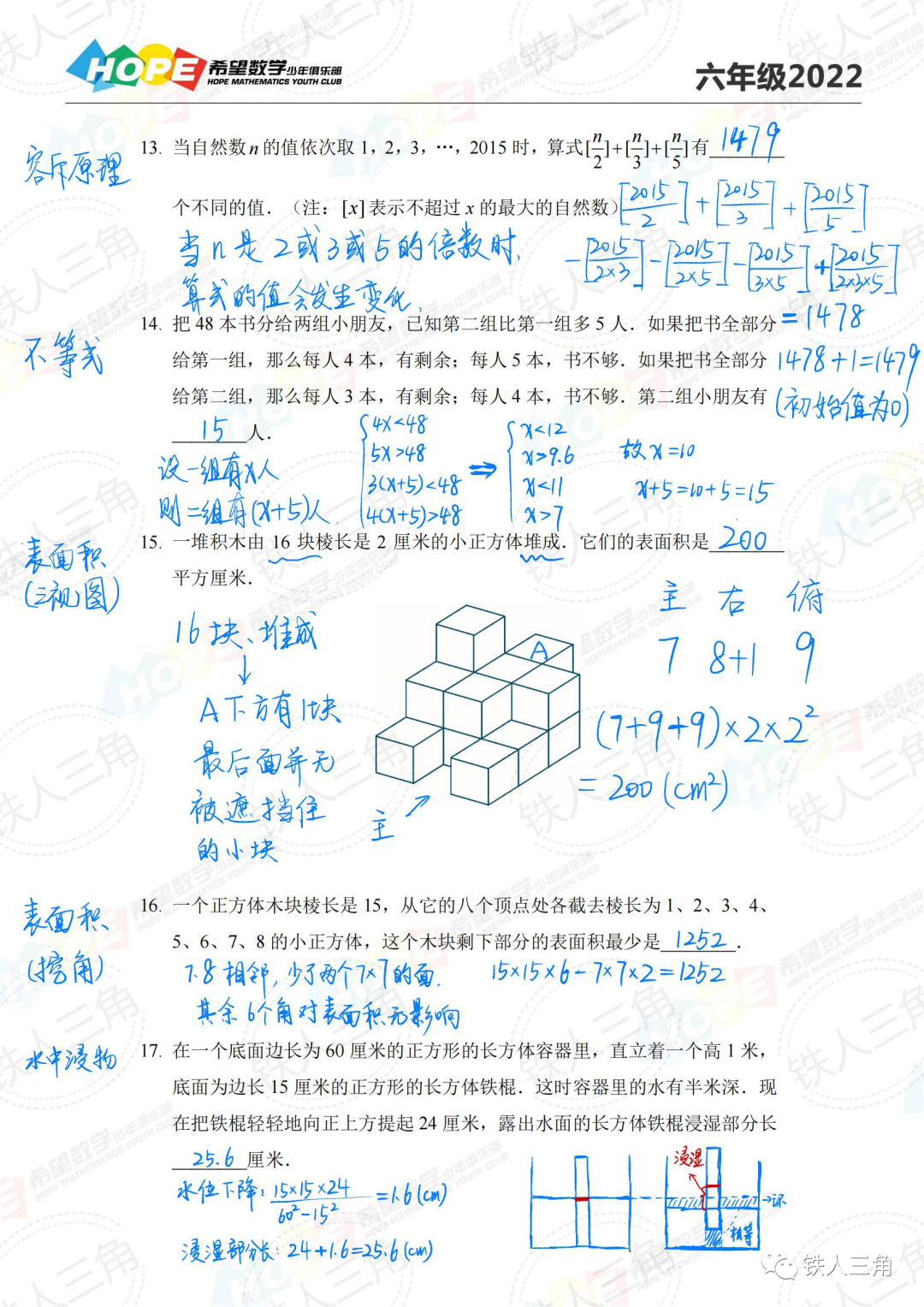
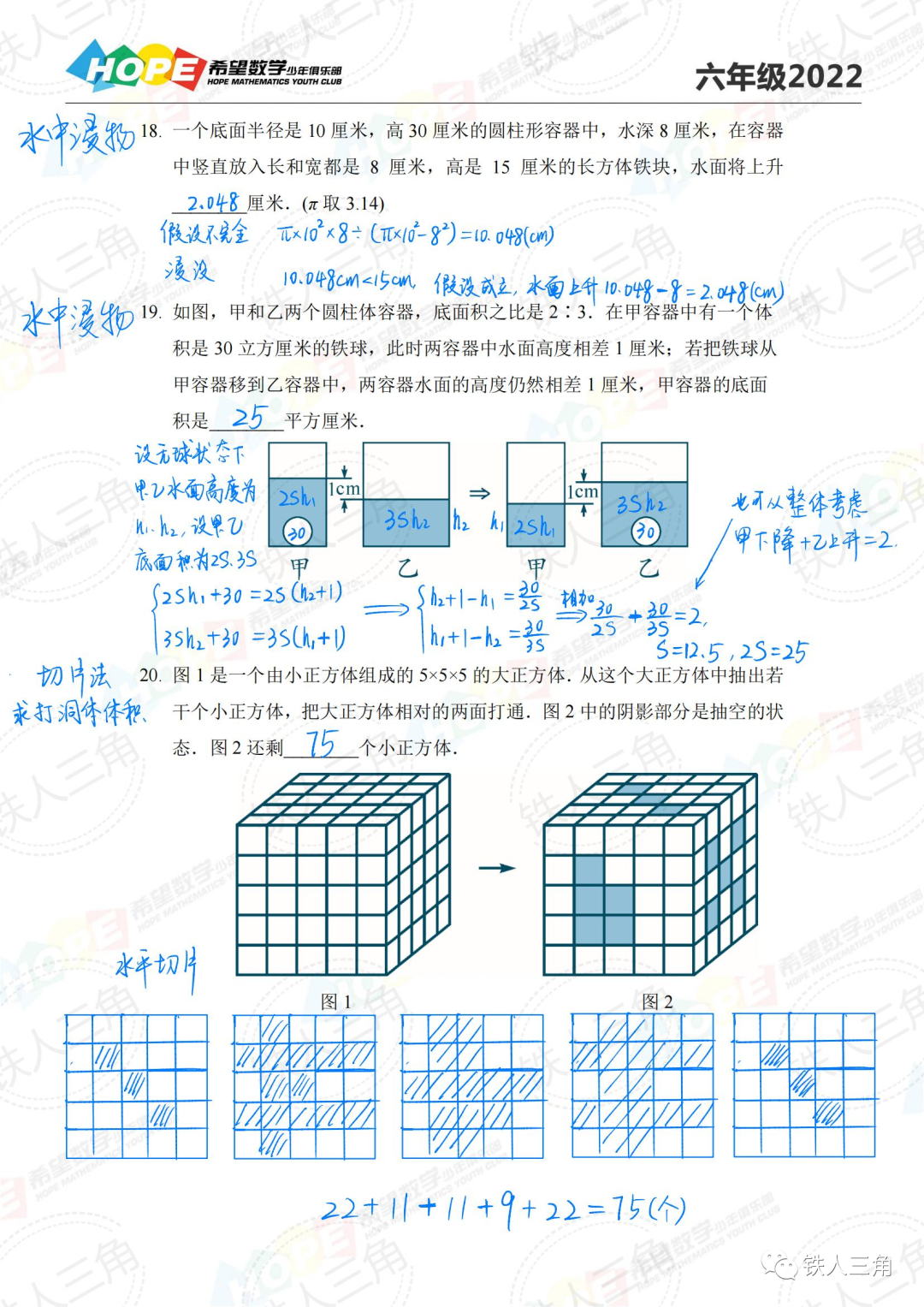

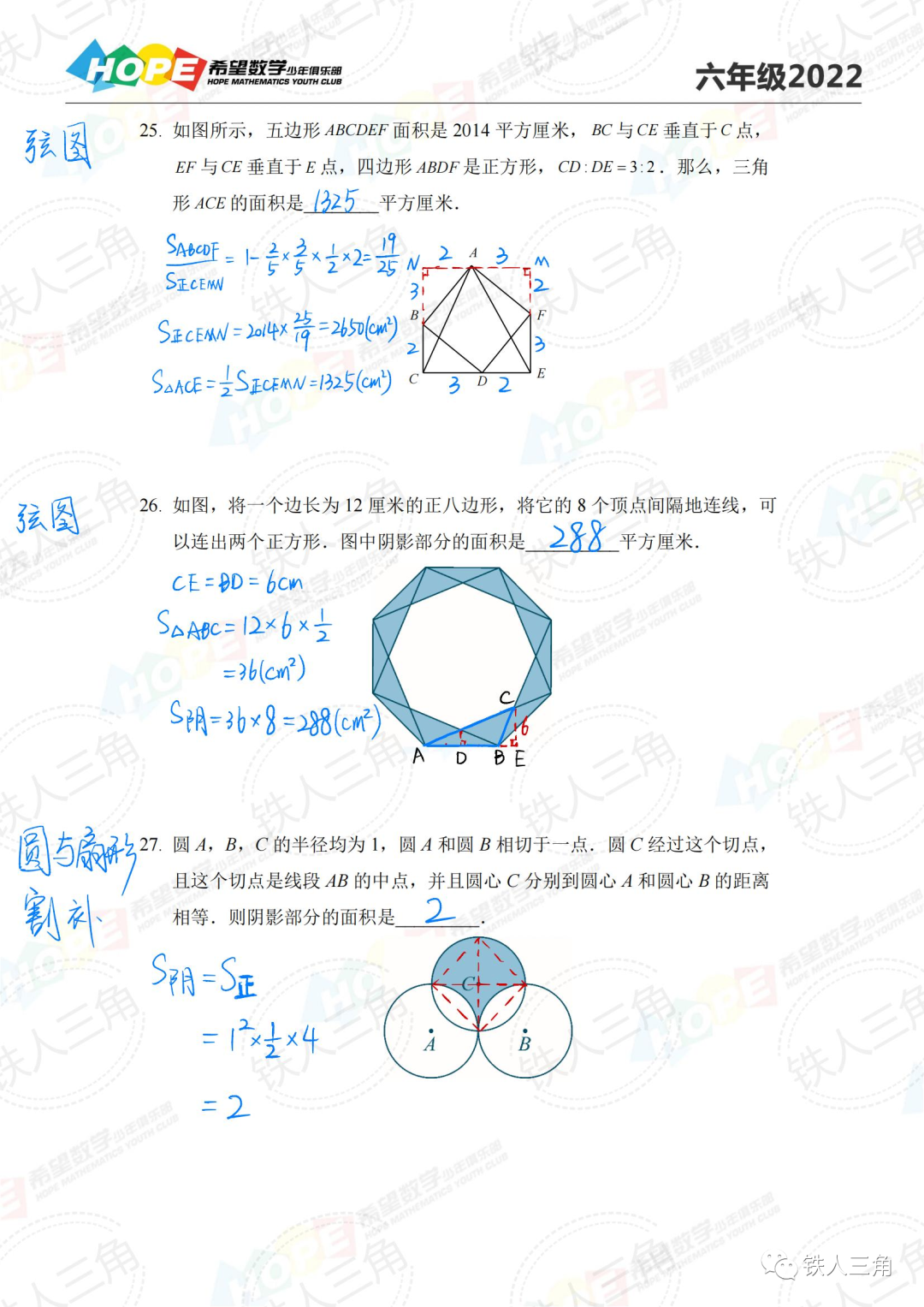





左右滑动查看更多

49-100题解析








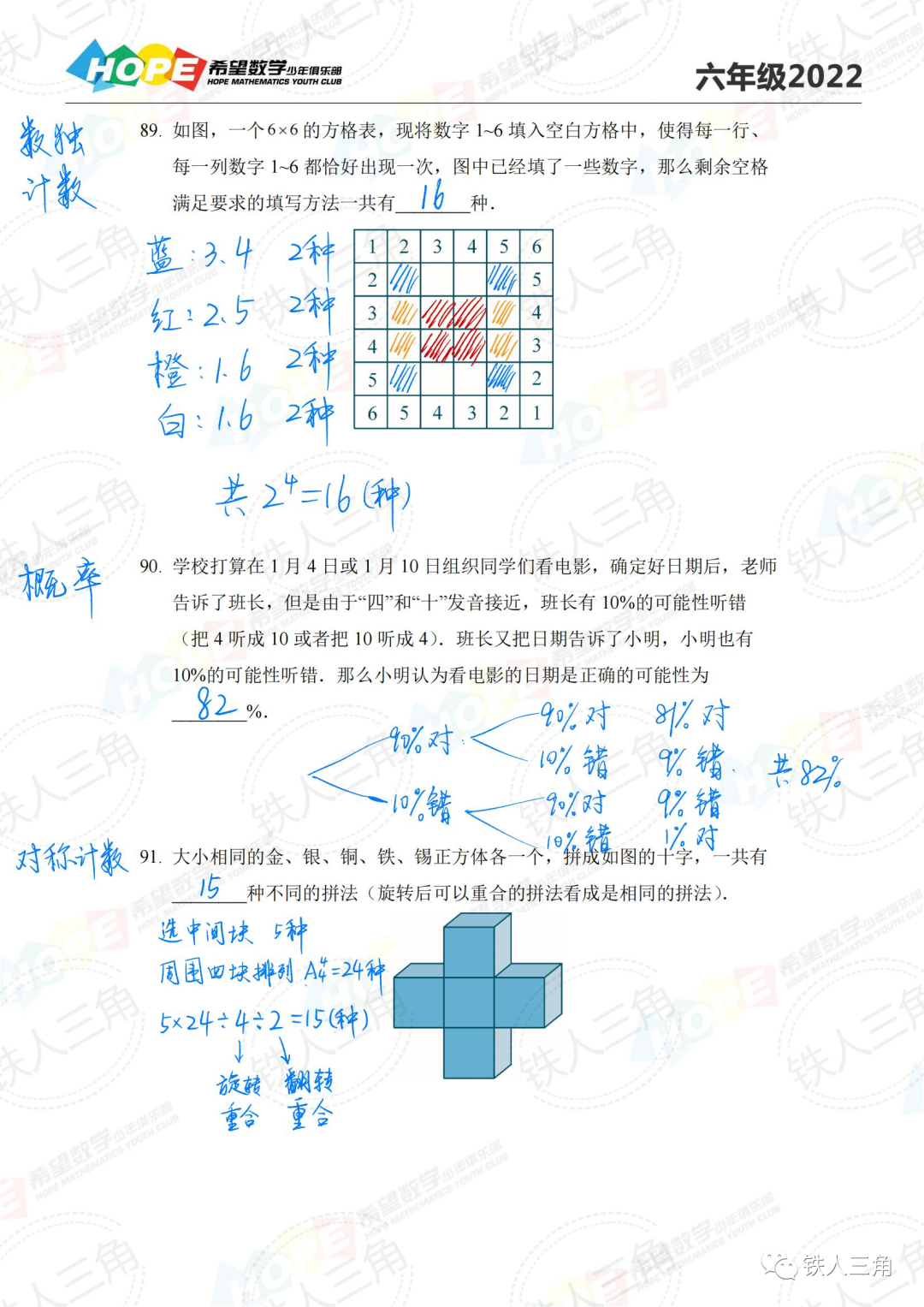
知识点分布梳理
计算
1、裂项:常规分数裂项及较少出现的阶乘裂项
2、循环小数:涉及循环小数化分数,相对基础
3、繁分数运算:结合换元思想,相对基础
4、比较与估算:难度较大,需要掌握常见的放缩技巧
5、定义新运算:与归纳相结合,形式灵活
6、数字谜:与数论中的整除、完全平方数相结合,难度较大
几何
1、格点与割补:掌握基本割补思想
2、等积变形:能根据平行的条件想到对应的方法
3、比例模型:综合性较强,需要熟练掌握各模型
4、勾股定理与弦图:出现多次,需要熟练掌握勾股数,以及对弦图相对敏感
5、圆与扇形:掌握基本周长面积公式,有基本割补思想
6、堆体表面积:相对基础,三视图带凹槽
7、正方体的表面:需掌握不同位置挖块对于正方体表面积的影响,结合最值考查
8、打洞体体积:相对基础,会使用切片法
4、水中浸物:出现次数多且难度较大,需要较强的基本功
应用题
1、代数思想:多个问题涉及方程(组)、不等式(组),代数能力强占优
2、分数比例应用题:模型相对基础,需要有基本的对应能力、份数思想、代数思想
3、工程问题:出现多次,考查全面,代数基本功过硬的话难度不大
4、浓度问题:相对基础,代数基本功过硬的话难度不大
行程
1、平均速度:相对基础,需掌握平均速度的概念
2、v-t图:相对基础,需要有基本的识图能力
3、环形跑道:涉及走走停停与变速变向,难度较大
4、接送问题:需要掌握最基本的接送问题处理方法
数论
1、弃九法:出现多次,结合计算、最值等综合考查
2、整除特征:与逻辑推理相结合,需熟练掌握常见数的整除特征
3、位值原理:题目特征相对明显,需要一定基础以便于识别出题目类型,通常与其他数论知识点一起考查
4、最大公因最小公倍:题目灵活,考查全面,需掌握短除模型、辗转相除法等基本方法,以及分数的最大公因最小公倍求法
5、因数个数定理:给定因数个数反推原数的类型居多
6、同余问题:相对基础,掌握基本方法即可
7、剩余问题:相对基础,掌握基本方法即可
8、完全平方数:出现次数较多且难度较大,需要熟练掌握完全平方数的各种性质
计数
1、枚举法:多个综合题目涉及枚举的思想方法
2、容斥原理:结合数论模块知识点考查
3、加乘原理与排列组合:着重考查分类的意识,需要熟练掌握基本的类型和对应技巧(如染色、捆绑法等)
4、对称性计数:难度不大但易错,需要思考全面
5、图形计数:难度不大但易错,需要思考全面
6、概率:相对基础
组合
1、逻辑推理:出现次数较多,多数结合数论知识分析,难度较大
2、最值问题:出现次数较多,需熟练掌握最值原理,并具备极端思想与局部调整的能力
3、操作类:难度较大,需要具备较强的归纳能力
4、必胜策略:结合数论知识
5、构造论证:论证部分偏少,出现黑白染色的遍历问题,多数题目考查极端构造
6、数独:结合计数考查,相对新颖
总体来说,100题的题目综合性强、思维难度较大、计算量大,考察单一知识点的题目很少,多数题目都涉及多个知识点甚至多个模块。需要学生在各模块的学习中都打下良好的基础,并适当加以练习,做到熟能生巧、融会贯通。




全部 0条评论