纵观这几年早培初赛考试，具体变化如下：

（1）从最初的只考奥数逐渐加入了神测、文常和英语等，知识面覆盖扩大；

（2）从最初线下的一场测试45分钟转变为网络测试（一般三场），综合性不断提高；

（3）题型从最初的选择题到2021年的填空题的转变，且有的题明确要求写成小数形式，有的明确要求写成分数分子分母之和的形式，难度加大；

（4）神测题目逐渐减少，公开课新题型增多，对学生解决实际问题的能力不断提高。

2022年人大附早培时间轴如下：

        7.16-7.18，线上报名

        7.21，线上全真模拟

        7.23，早培线上初赛（16000人左右）

        7.25，早培线上复赛（3000人左右）

        7.28，早培入营（600人左右）

        8.1，早培录取（160左右）

     

解释几个大家比较关心的问题：

1、北京市户籍海淀区五年级学生到底是户籍在海淀，还是学籍在海淀。结论是不知道。

我们纵观近几年政策变化，招生范围都在缩小，今年不知道范围如何，但是有北京市户籍的海淀区在读五年级学生，肯定都建议备考一下。

2、早培不保直升人大附高中，会在四年之后重新评价。

早培优点也很多，能提前上岸，能够让孩子和学习最优秀的同龄孩子一起学习。即便觉得学习难度大，也可以进入人本，高中虽然不100%保证，但是不掉队机会还是很大的。

3、全真模拟虽然不计入成绩，但是必须参加，不参加视为放弃考试资格。

4、没有提九年一贯制。

5、网上预估初试人数16000人左右，实际入学约140人。录取率不足1%。这其实还是锁区导致报名人数降低，2021的录取率更夸张到了0.5%（网络数据）

附：早培数学真题（第一场）

1.已知甲校原有学生1016人，乙校原有学生1028人，寒假期间甲、乙两校学生人数变动的原因只有转出与转入两种，且转出的人数比为1：3，转入的人数比也为1：3。若寒假结束开学时甲、乙两校学生人数相同，则乙校开学时有学生（1010)人

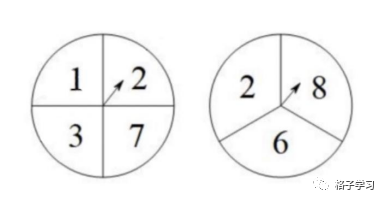
2.如图所示，甲乙两人准备了可以自由转动的转盘A、B。每个转盘被分成几个面积相等的扇形，并在每个扇形内标上数字。如果任意转动A、B两个转盘，将指针所指的数字相加，和是质数的可能性是  ，那么m+n=?

m+n=17      

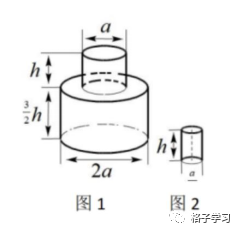
3.如图1中的瓶子盛满了水，如果将这个瓶子中的水全部倒入图2的杯子中，那么一 需要几个这样的杯子？(瓶子和杯子的厚 只略不计）需要28个这样的杯子       

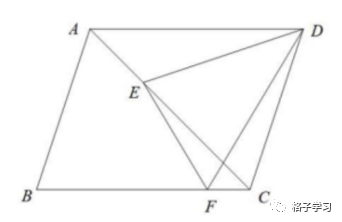
4.如图所示，平行四边形ABCD的面积是48平方厘米，AC=3AE，BC=4FC。△DEF的面积是多少平方厘米？

面积是14平方厘米。  

5.某商店在奥林优克官方旗舰店开启预定的第一天，成功向旗舰店预定了“冰墩域系列和雪容融的数量之比是7；8接着在第二天预定的时候“有成功预定了这两种系列一共41件此时冰墩墩系列和雪容融系列数量之比为15；17'第一天和第二天都只预定不售出，第三天的时候该店开始卖出的同时，继续预定。该店在第三天的售出和预定结束后统计得知，比第二天的吉祥物数量净增14件，此时冰墩墩系列和雪容融系列的数量之比变为8：9。则在第三天销售和预定结束后“冰墩墩”系列的数量为（880）件。

6..已知两个数x、y满足2x-3y=4，并且x≥-1，y≤2，现有k=x-y，则k的最大值与最小值之和是4

7.王老师在黑板上写了若干个连续自然数1.2.3........ ，然后擦去其中的三个数，已知擦去的三个数中有且只有两个质数。若剩下数的平均数是19，那么王老师擦去的两个质数的和最大是？

王老师擦去的两个质数的和最大是60

8.设p，q是任意两个大于100的质数，那么p²-1和q²-1的最大公约数的最小值是 24

9.一辆客车，一辆货车和一辆小轿车在同一条直线上朝同一方向行驶，在某一时刻，货车在中，客车在前，小轿车在后，且它们的距离相等，走了15分钟，小轿车追上了货车又走了5分钟，小轿车追上了客车，问再过10 分钟，货车追上了客车。

10.某公司在农村租用了720亩闲置土地种植了A、B和C三种茶树。为达到最佳种植效益，要求终止A茶树的面积是B车数面积的2倍CC茶树的面积不得超过A茶树面积的1.4倍，但种植A茶树的面积不得超过270亩。到茶叶采摘季节时，该公司聘请当地农民进行采摘，每人每天可以采摘0.4亩A茶叶或者采摘0.5亩B茶叶，或者采摘0.6亩C 茶叶。或若该公司聘请批农民恰好20天能采摘完所有茶叶，则种植A茶树的面积是 260 亩。

11.从1，2， 3.…，50这50个正整数中任取n个数，在这n个数中总能找到3个数，它们两两互质，则n的最小值为3

12.将4个数1. 3. 6. 8写成一行并进行如下操作：对每一对相邻的数，用右边的数减去左边的数，然后将所得之差（可以是负数)写在这两个数之间，算是完成了一次操作。然后再对这个由7个数排成一行的数进行同样的操作。如此继续下去，共操作100次，那么最后得到的一行数的和为718 。

13.为保障某贫困山区小学的学生有充足的学习文具，某小区向住户募集了2360支钢笔，1040本笔记本和若干套尺规套装，小区工作人员将这些物资分成了甲、乙、丙三类包裹进行发放，一个甲类包裹里有25支钢笔，10本笔记本和4套尺规套装，一个乙类包裹里有16支钢笔，8本笔记本和7套尺规套装，一个丙类包裹里有20支钢笔，6本笔记本和3套尺规套装。已知甲、乙、丙三类包裹的数量都为正整数，并且甲类的个数低于28个，乙类个数低于106个，那么所有包裹里尺规套装的总套数为751