2020鹏程杯数学试题及解法(五年级)

一、填空题(1~10题)
- 1 -
两个质数与1之和等于2020,则这两个质数的积等于________.
【答案】4034.
【解析】a + b + 1 = 2020,a + b = 2019,a、b为一奇数一偶数,偶数为唯一的偶质数2,奇数为2017,乘积2 × 2017 = 4034.
- 2 -
2.一颗参天大树,树干周长为3米。地上有一根常青藤恰好绕了它5圈,藤尖离地面20米高那么,这根常青藤至少有________米.
【答案】25.
【解析】树干作为圆柱体,绕了5圈,说明水平方向转动了5圈,即3 × 5 = 15米,高为20米,说明竖直方向上升了20米.根据勾股定理,勾3股4弦5,15和20分别是3和4的5倍,所以虅长是弦5的5倍,为25米.
- 3 -
若正整数n使得3n – 4,4n – 5和5n – 3都是质数,则这三个质数的乘积等于________.
【答案】42.
【解析】(5n – 3) – (3n – 4) = 2n + 1,为奇数,故3n – 4和5n – 3奇偶性不同,其中小的那个是偶质数2,故3n – 4 = 2,n = 2,此时3个数为2,3,7,乘积2 × 3 × 7 = 42.
- 4 -
4.被2,3,4,5,6除都余1且被7整除的自然数中最小的一个是________.
【答案】301.
【解析】这个数除以2,3,4,5,6余1,那么这个数减1就是2,3,4,5,6的公倍数,就是60的倍数,
所以这个数可以为61、121、181、241、301、……;第一个7的倍数是301.
- 5 -
如图,在一个大正方形纸片中,剪出两个带阴影的正方形:一个为甲,另一个为乙.已知甲的面积是16 cm², 则乙的面积是________ cm².
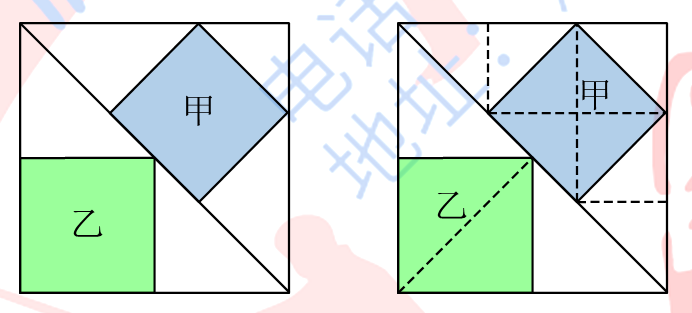
【答案】18.
【解析】甲为右上三角形的4/9,乙为左下角三角形的2/4 = 1/2,甲∶乙 = (4/9):(1/2) = 8:9,故乙为16 ÷ 8 × 9 =18 cm².
- 6 -
甲、乙汽车分别从A,B两站同时出发相向而行,两车第一次在距A站32千米的C处相遇,相遇后两车继续行进,各自到达B,A两站后,立即沿原路返回,第二次在距A站64千米的D处相遇,则A,B两站的距离是________千米.
【答案】80.
【解析】设全程为x千米,分析甲、乙、甲 + 乙在各段的行程:

- 7 -
一队少年儿童不超过50人,围成一圈做游戏,每个儿童的左、右相邻的都恰是一个男孩和一个女孩.则这队少年儿童最多有________人.
【答案】48.
【解析】设有一个男生,左右为一男一女,不妨设左边为男生,即环形队列以“男男女”开始,则接下来可以推导出依次是女男男女女……,4人一个循环,连接上开头,故人数为4的倍数.50以内4的倍数最大是48.
- 8 -
一个长方体,长 : 宽 = 2 : 1,宽 : 高 = 3 : 2.如果长方体所有棱长之和是220厘米,则长方体的体积是________立方厘米.
【答案】4500.
【解析】化公比,长 : 宽 : 高 = 6 : 3 : 2,又长 + 宽 + 高 = 220 ÷ 4 = 55,
可解得长 = 30,宽 = 15,高 = 10,体积为30 × 15 × 10 = 4500(立方厘米).
- 9 -
战斗在抗击“新冠肺炎”第一线的钟南山院士出生的公元年份数是个完全平方数,那么今年(2020年)钟院士已经是________岁高龄.
【答案】32.4
【解析】小于2020的平方数一次为1936、1849、……,显然1936是一个合理的年份,
钟院士的年龄为2020 – 1936 = 84(岁).
- 10 -
由一条公路对A,B,C,D四个居民点依次开通四条道路(如图).已知沿道路→公路→道路移动,由A到B的路程等于9千米,由A到C的路程等于13千米,由B到C的路程等于8千米,而由B到D的路程等于14千米.则由A到D的路程等于________千米.
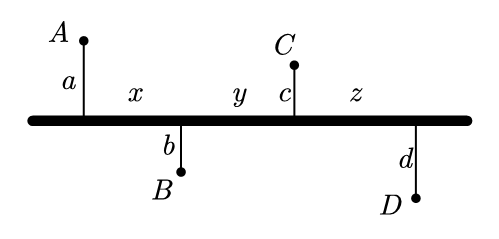
【答案】19.
【解析1:代数法】
把公路上的3段分别标为x,y,z,根据题意可知:
a + x + b = 9,……①
a + x + y + c = 13,……②
b + y + c = 8,……③
b + y + z + d = 14,……④
待求的A到D的路程为a + x + y + z + d,不包含b和c,故可先将方程组中的b、c消去,
c只出现2处,最少,可以先消去c,② – ③得:
a + x – b = 5……⑤
把⑤式分别与①式和④式相加,可以消去b,发现与④相加直接得到
a + x + y + z + d =19(千米).
【解析2:直接分析】
AD = AC – BC + BD = 13 – 8 + 14 = 19(千米).
二、解答题(11~15题)
- 11 -
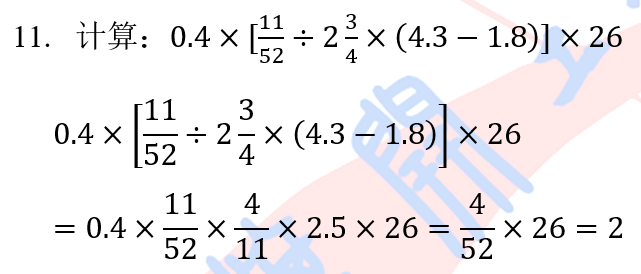
- 12 -
⑴ 试将505写成10个连续自然数之和;
⑵ 能将2020写成10个连续自然数之和吗?如果能,把它写出来;如果不能,说明理由.
解:⑴ 505 = 101× 5 = (50 + 51) × 5 = 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55.
⑵ 不能.
设10个连续自然数为a,a + 1,a + 2,……,a + 9,其和为10a + 45 为奇数,不可能为2020.
- 13 -
小明在一张平面曲边薄板的边缘上选取5个点A、P、B、C、D,如图所示.已知AB//DC且AB = DC.连接PD交AB于E,连接PC交AB于F,连接EC.已知⊿PAE的面积为1.5,⊿PBF的面积为2.5,求⊿CEF的面积.
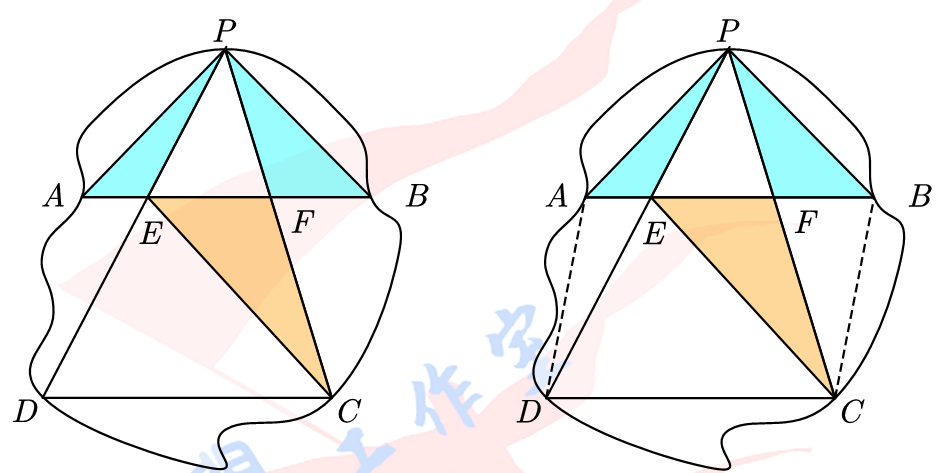
【答案】4.
【解析】本题主要考察对平行四边形的一半面积的图形的熟悉程度.
⑴ 你能看出来S⊿PDC - S⊿PAB是平行四边形ABCD面积的一半么?若能,则:
S⊿PCD = S⊿PAB + S⊿DEC,
去掉S⊿DEC得:S⊿PCE = S⊿PAB,
去掉⊿PEF得:S⊿CEF = S⊿PAE + S⊿PFB = 4
⑵ 你能看出来S⊿PAD + S⊿PBC是平行四边形ABCD面积的一半么?
你能看出来S⊿ADE + S⊿BCE也是平行四边形ABCD面积的一半么?
去掉公共部分,得:S⊿CEF = S⊿PAE + S⊿PFB = 4
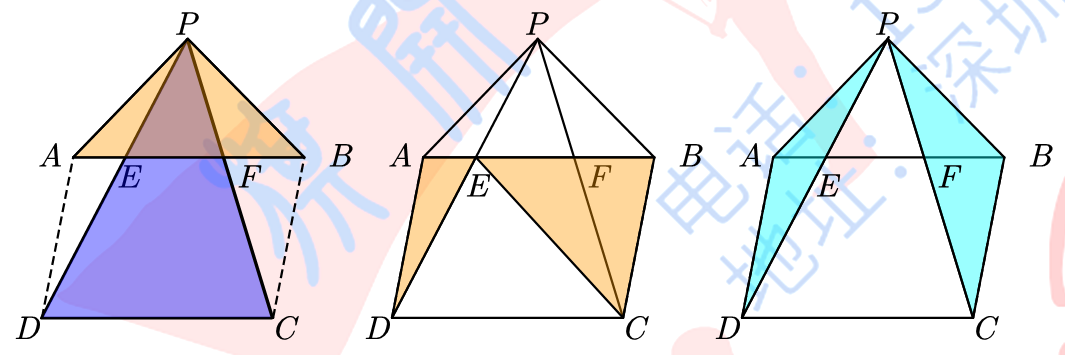
为什么S⊿PDC - S⊿PAB,S⊿PAD + S⊿PBC和S⊿ADE + S⊿BCE都是平行四边形ABCD面积的一半?
请聪明的你自己探索吧!
- 14 -
对于任意的n个自然数,总能选出其中的4个数a,b,c,d,使得(a – b)(c – d)被2020整除.试确定n的最小值,简述你的理由.
【答案】102.
【解析】本题考查抽屉原理.2020 = 101 × 20.当有102个自然数时,它们除以101的余数只有101种情况,
所以必有两个数余数相同,不妨设为a、b,则(a – b)是101的倍数,
去掉a、b,此时还剩下100个数,它们除以20的余数有20种情况,
所以至少有2个相同,不妨设为c,d,则(c – d)是20的倍数,
故(a – b)(c – d)是2020的倍数.
若只有101个数,我们取1~101,发现没有一个差是101的倍数,
所以(a – b)(c – d)也不能是2020的倍数,101个数是不行的.
综上所述,n的最小值为102.
- 15 -
100人参加象棋单循环赛,每两人都对弈一局且决出胜负.
⑴ 求总共对弈多少局?
⑵ 证明:比赛结束后,一定可以将这 100个人列为一队,使得队列中的每一个人都战胜了紧跟在他后面的那个人!
解:⑴ 100 × (100 – 1) ÷ 2 = 4950.
⑵ 证明,用一步一步增加人数的方法:
① 先在100个人里任选2人,将2人按胜者在前排列,即符合“每一个人都战胜了紧跟在他后面的那个人”的要求,队列可记为a₁,a₂;
② 再从剩余的人中任选一人,若其战胜了a₁,则排在a₁前面;若其输给a₁,战胜了a₂,则排在a₁和a₂之间,若其输给了a₂,则排在最后;我们把新的队列重新按顺序记为a₁,a₂,a₃,其仍然符合“每一个人都战胜了紧跟在他后面的那个人”的要求.
③ 用②的方法逐个往队列里面加人,直到把所有的人都排入队列,这个队列满足“每一个人都战胜了紧跟在他后面的那个人”的要求.
得证.

① 华杯赛/华数之星真题试卷-解析版 附详细解题过程
② 迎春杯/青少年创新能力测试-解析版 附详细解题过程
③ 希望杯/希望数学-解析版 附详细解题过程
④ YMO世界青少年奥林匹克数学竞赛-解析版 附详细解题过程
⑦ 美国数学大联盟杯-解析版 附详细解题过程
⑧ 鹏程杯-解析版 附详细解题过程
⑨ 历年全国小数测初评、终评真题及答案解析
② 朗思 iESOL 备考资料
② 深圳小学各科上/下学期单元测试、期末真题及答案解析
② 深圳初中入学测试、月考、期末真题及答案解析(上、下学期)
② 深圳高中各科入学测试、月考、期末真题及答案解析
添加 家长论坛微信



全部 0条评论