开始要给大家分享的是 AMC 10 几何板块的 5 大定理。

在这一阶段的课内学习中，几何部分主要包括了相似三角形 (similar triangle), 全等三角形 (congruent triangle), 勾股定理 (Pythagorean theorem), 正弦 (the law of sines)、余弦定理(the law of cosines), 圆 (circle) 等主要知识点。

👇 5 大定理请熟记于心：

1.平行线分线段成比例定理

2.射影定理 (Euclid's theorem)

3 角平分线定理 （Angle bisector theorem）

4 利用正弦求三角形面积 

5 斯图尔特定理（Stewarts theorem）

1

平行线分线段成比例定理

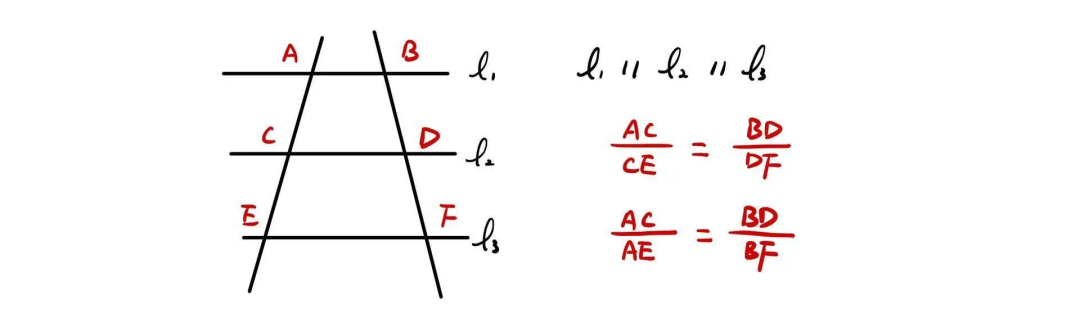
这一定理不仅仅适用于相似三角形，其核心思想是找到两到三组平行线，利用平行线分割的线段找出比例关系。

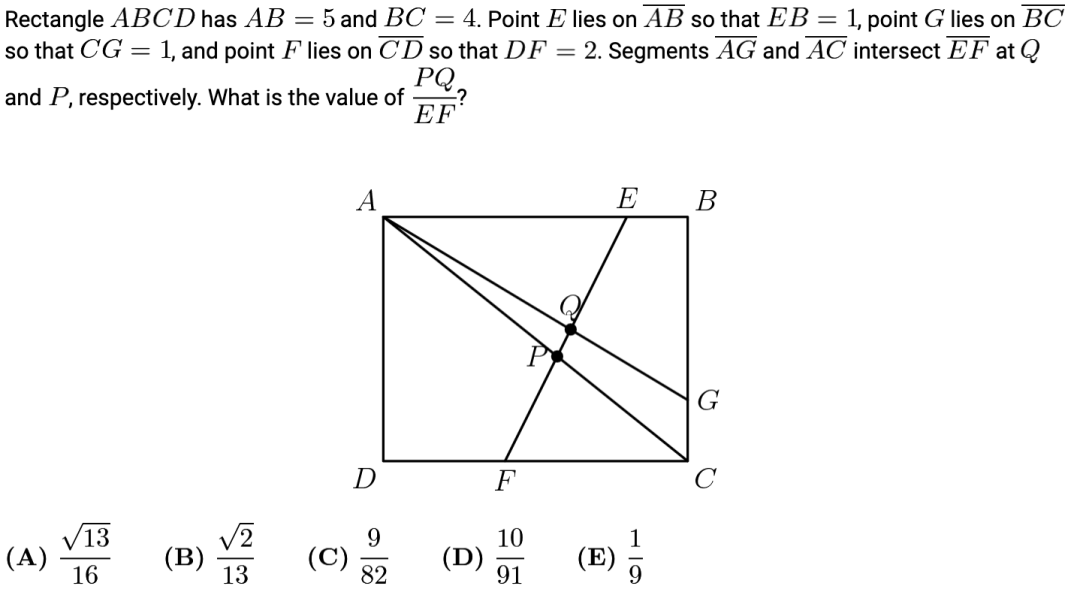
例如下面这道题，你可以根据平行线找出比例关系么？

AMC 10B 2016 Q19 （答案见最后）

2

射影定理 (Euclid's theorem)

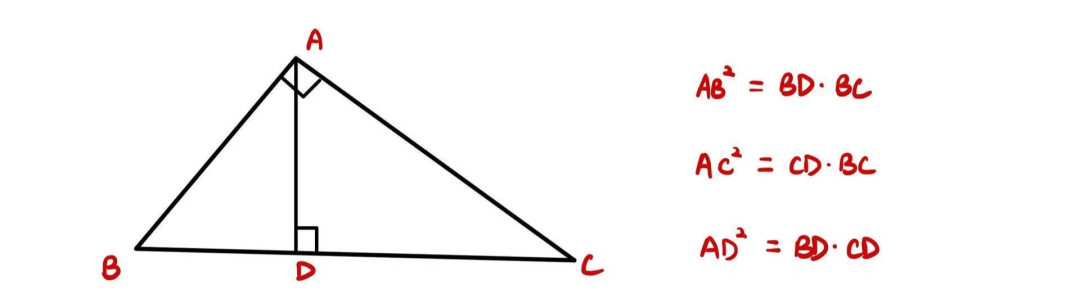
这一定理的结论可以通过中学学习的相似三角形的知识证明。是和直角三角形相关的题目的重要解题线索，使用时，只需要找出一个直角三角形和其斜边的高，就可以对未知边长进行求解。

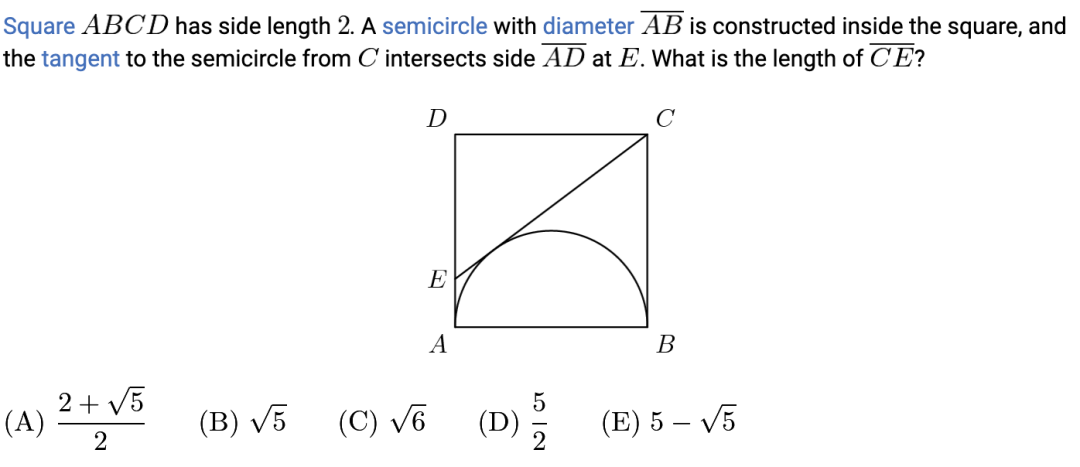
下面这道题中，如果想应用射影定理，你找出需要的直角三角形了吗？

AMC 10B 2004 Q22 （答案见最后）

3

角平分线定理 （Angle bisector theorem）

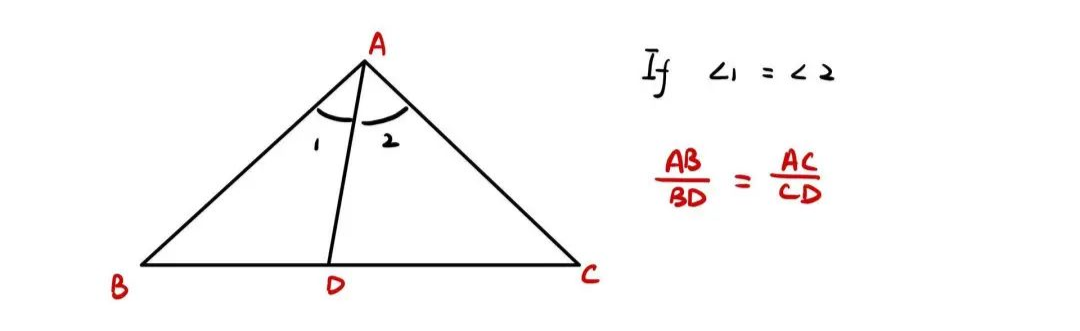
这一古老的几何定理早在公元前 300 年就出现在了几何原本的第六卷中。是一个在 AMC10 的几何难题中颇为实用的定理。看到了角平分线的信息，就可以找出线段之间的比例关系。

掌握了这样一个定理，即便是 AMC10 的压轴题也不在话下。

AMC 10A 2018 Q24 （答案见最后）

4

利用正弦求三角形面积 

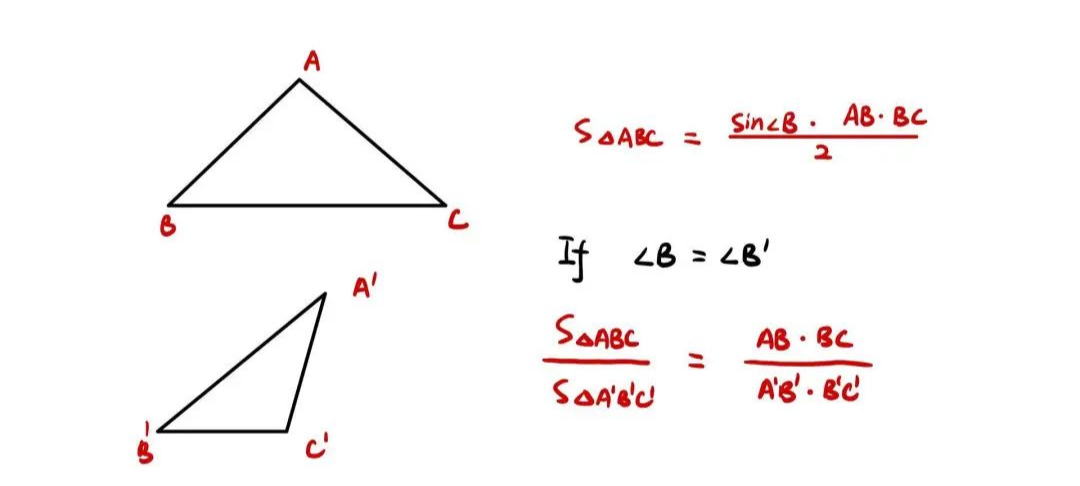
这一结论也是针对中学三角知识的延伸，不仅仅可以求三角形的面积，还可以在已知两个三角形其中一个内角相等的前提下，找出对应边长的比例关系。

了解这一公式，是不是对上面的第三题又有了新的思路呢？不仅如此，在其他的 AMC 考题中我们也可以找到它的应用。

AMC 10B 2017 Q19 （答案见最后）

5

斯图尔特定理（Stewarts theorem）

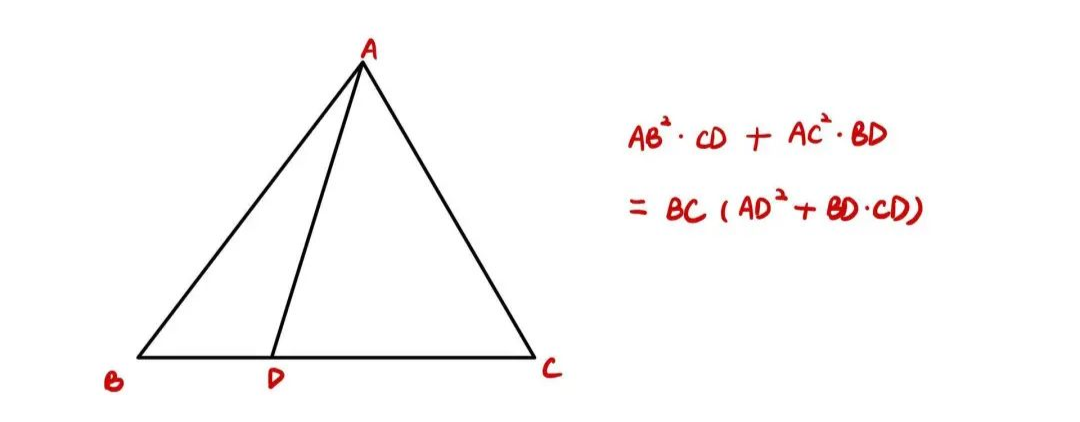
这个定理不太好记，当 D 点为中点时还可以简化为中线定理。作为比较不常用的定理，适合针对最后五题复习的同学。

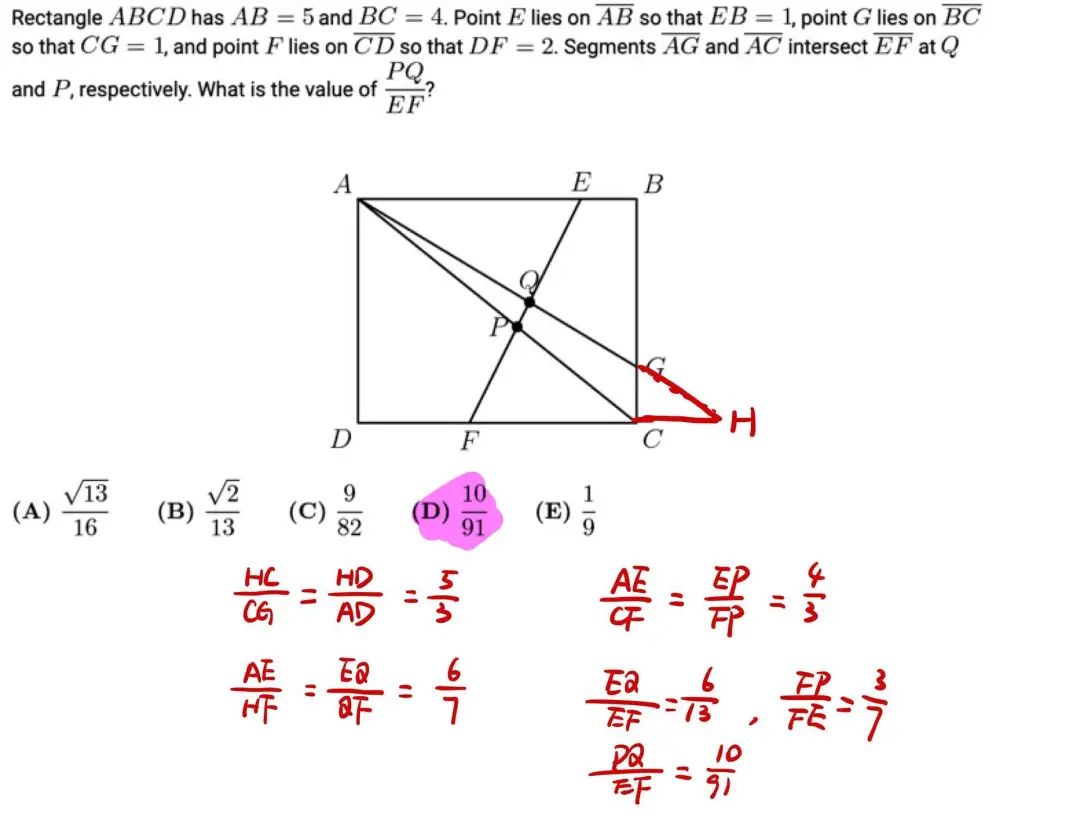
试着用这个定理一起挑战一下这道 13 年的几何压轴题吧！

详细过程及答案