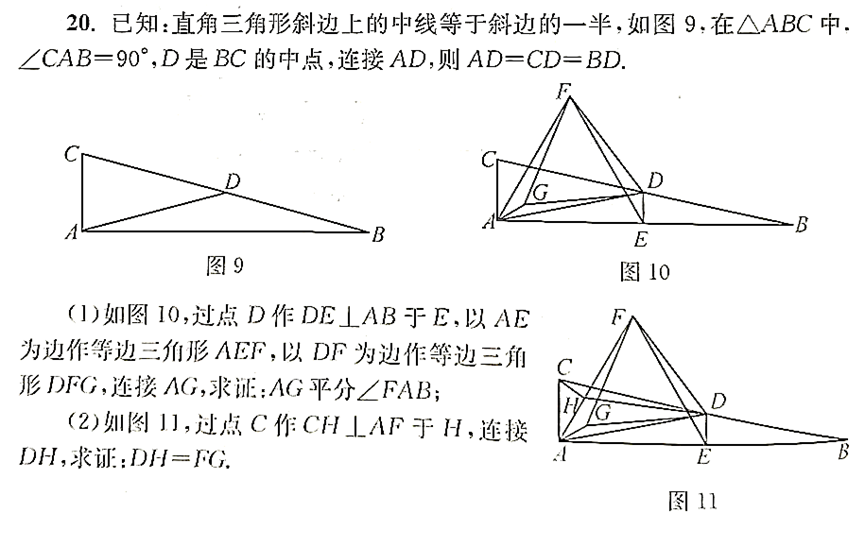
题目不算多大难题，只要线索找准了，基本上就无压力了；

题干给的是直角三角形斜边中线等于斜边一半的这条性质，其实能学到这里的同学都已经知道了；

（1）那么第一小题要证明AG平分∠FAB，我们知道∠FAB是60°，既然是平分，那么只要能得到分出来的两个角都是30°即可；

根据2个等边三角形绕同一顶点，很容易联想到对应边相等来构造全等，即△FAG≌△FED，过程不写了，常见类型；

∴可得∠FAG=∠FED

而∠FED和∠AEF这个60°的角刚好组成了90°

∴可得∠FED=30°

则∠FAG=30°

那么∠BAG=∠BAF-∠FAG=30°

∴AG平分∠FAB；

（2）这一小题在原来的基础上多了一个垂线CH；

要证明DH=FG，根据图形很容易想到△CDH和△AFG，但是两个三角形的边CD和AF明显不等，∴它们全等不现实

那么就是全等找的不对

观察FG，

FG是等边三角形△FGD的边，那不就可以转换吗

∴只要DH和DG或者FD相等就行

而FD在△FDE中，这个三角形和△FAG是全等的，刚才已经确认△FAG不行

∴这个△FDE也不行

那么我们用排除法解决了2个可能，就只剩下DG这条线段了

DG在△ADG中

AD=CD，AG=DE=AC/2

而CH在Rt△ACH中，可得CH=AC/2

∴AG=CH

现在两个对应边相等了，就差夹角了

∠HCD和∠GAD是否相等呢？

这道题唯一的难点就在这，倒角有点麻烦

先看∠GAD

∠GAD=30°-∠DAE

而∠DAE=∠B

∴∠GAD=30°-∠B

再来看∠HCD

∠HCD和60°的∠ACH组成了∠ACB

∴∠HCD=∠ACB-60°

而∠ACB=90°-∠B

∴可得∠HCD=30°-∠B

则∠GAD=∠HCD

那么△CDH≌△ADG成立

则DH=DG

结合DG=FG

可得DH=FG；