2021 CSP-S(提高级)认证第一轮试题及详细解析

单选选择答案

1A	2B	3A	4C	5C	6C	7C	8B
9D	10A	11A	12C	13C	14C	15B

一、单项选择题（共15题，每题2分，共计30分，每题仅有一个正确答案案）

1.在 Linux 系统终端中，用于列出当前目录下所含的文件和子目录的命令为（ ）。

A. ls   B. cd   C. cp   D. all

【解析】Linux系统中：ls 命令用于显示指定工作目录下之内容（列出目前工作目录所含之文件及子目录)；cd 命令用于切换当前工作目录；cp 命令主要用于复制文件或目录；all只是用来凑数的，没什么实际意义。

2.二进制数 001010102 和 000101102 的和为（ ）。

A. 001111002 B. 010000002    C. 001111002   D. 010000102

【解析】这是一个最基本的二进制加法，出现了连续的进位算出来是 010000002

3.在程序运行过程中，如果递归调用的层数过多，可能会由于（ ）引发错误。

A. 系统分配的栈空间溢出

B. 系统分配的队列空间溢出

C. 系统分配的链表空间溢出

D. 系统分配的堆空间溢出

【解析】递归需要使用到系统堆栈空间，如果递归层数过多，导致系统堆栈空间不足。

4.以下排序方法中，（ ）是不稳定的。

A. 插入排序 B. 冒泡排序 C. 堆排序 D. 归并排序

【解析】待排序的记录序列中可能存在两个或两个以上关键字相等的记录。排序前的序列中Ri领先于Rj（即i<j）.若在排序后的序列中ri仍然领先于rj，则称所用的方法是稳定的。比如int数组[1,1,1,6,4]中a[0],a[1],a[2]的值相等，在排序时不改变其序列，则称所用的方法是稳定的. (插入排序、冒泡排序、二叉树排序、二路归并排序及其他线形排序是稳定的;选择排序、希尔排序、快速排序、堆排序是不稳定的）.<="" span="">

5.以比较为基本运算，对于 2n 个数，同时找到最大值和最小值，最坏情况下需要的最小的比较次数为（ ）。

A. 4n−24n−2   B. 3n+13n+1    C. 3n−23n−2   D. 2n+12n+1

【解析】比较可以分解成3步来进行：第一步先将2n个两两比较n次将数字分为两组:含有最大值的较大值一组与含有最小值的较小值一组；第二步在较大值组中进行n-1次比较得出最大值；第三步在较小值组中进行n-1次比较得出最小值，总共 n + n-1 + n-1 = 3n-2次。

6.现有一个地址区间为 0 到 10 的哈希表，对于出现冲突情况，会往后找第一个空的地址存储（到 10 冲突了就从 0 开始往后），现在要依次存储 (0,1,2,3,4,5,6,7) ，哈希函数为 h(x)=x²mod11 。请问 7 存储在哈希表哪个地址中（ ）。

A. 5     B. 6    C. 7    D. 8

【解析】对每个数分别计算一下，得出h(x)=(0,1,4,9,5,3,3,5) 。重复的调整一下 0,1,4,9,5,3,6,7 。

7.G 是一个非连通简单无向图（没有自环和重边），共有 36 条边，则该图至少有（ ）个点。

A. 8    B. 9     C. 10        D. 11

【解析】设有 n 个点，除了一个孤立点外剩下点为完全图。(n−1)*(n−2)/2=36解得 n=10

8.令根结点的高度为 1，则一棵含有 2021 个结点的二叉树的高度至少为（ ）。

A. 10    B. 11    C. 12     D. 2021

【解析】当树为完全二叉树时的高度为最小，所以 2¹⁰≤2021<2¹¹

0.前序遍历和中序遍历相同的二叉树为且仅为（ ）。

A. 只有 1 个点的二叉树

B. 根结点没有左子树的二叉树

C. 非叶子结点只有左子树的二叉树

D. 非叶子结点只有右子树的二叉树

【解析】前序遍历：先根再左子树后右子树，中序遍历：先左子树再根后右子树。所以去掉左子树时两个相同。

10.定义一种字符串操作为交换相邻两个字符。将 DACFEB变为 ABCDEF 最少需要（ ）次上述操作。

A. 7   B. 8    C. 9    D. 6

【解析】ADCFEB->ACDFEB->ACDEFB->ACDEBF->ACDBEF->

       ACBDEF->ABCDEF, 共 7 次 。

11.有如下递归代码

solve(t, n):

if t=1return1

elsereturn5 * solve(t-1,n) mod n

则 solve(23,23) 的结果为（ ）。

A. 1   B. 7   C. 12   D. 22

【解析】程序的运行结果为5²² mod 23,根据用费马小定理，在p为素数的情况下，a^p-1≡1（mod p），所以 5²²≡1(mod23)  。

12.斐波那契数列的定义为： F1=1,F2=1,Fn=Fn−1+Fn−2(n≥3) 。现在用如下程序来计算斐波那契数列的第 n 项，其时间复杂度为（ ）。

F(n):

if n<=2return1

elsereturnF(n-1) + F(n-2)

A. O(n)B. O(n²)C. O(2ⁿ)D. O(nlogn)

【解析】时间复杂度
f(n) = f(n-1) + f(n-2) 每一层都包含一个加法操作
例如n = 8时，T(n) = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5 + 2^6 = 2^7-1
O(n) = 2^7-1 = 2^n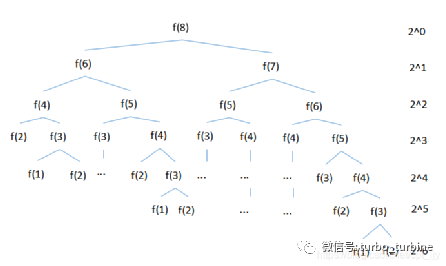

13.有 8 个苹果从左到右排成一排，你要从中挑选至少一个苹果，并且不能同时挑选相邻的两个苹果，一共有（ ）种方案。

A. 36    B. 48    C. 54    D. 64

【解析】只选 1 个苹果，有 8 种结果；选 2 个苹果，有 6+5+4+3+2+1=21 种；选 3个苹果，有 4+3+2+1+3+2+1+2+1+1=20种 ；选 4个苹果，有 5 种。

所以总 8+21+20+5=548+21+20+5=54 。

14.设一个三位数 n=a,b,c，其中 a,b,c均为 1 到 9 之间的整数，若以 a,b,c 作为三角形的三条边可以构成等腰三角形（包括等边），则这样的 n 有（ ）个。

A. 81    B. 120   C. 165    D. 216

【解析】考虑 a=b≠c 有几种。

1,1 无解。2,2 有 2+2−1−1=2 种。

同理，3,3 有 4 种，4,4 有 6 种，后面 5 到 9 都是 8 种。

所以 8×5+6+4+2=52 。

而 a=b=c 有 9 种。

所以 52×3+9=165 。

15.有如下的有向图，节点为 A, B, … , J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为（ ）

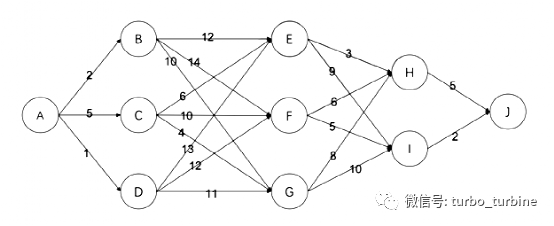
A. 16    B. 19   C. 20    D. 22

【解析】单源最短路径问题，没有负边权，可以用dijkstra算法模拟一下 。

二、阅读程序（程序输入不超过数组或字符串定义的范围∶判断题正确填√，错误填x∶除特殊说明外，判断题1.5分，选择题3分，共计40分）

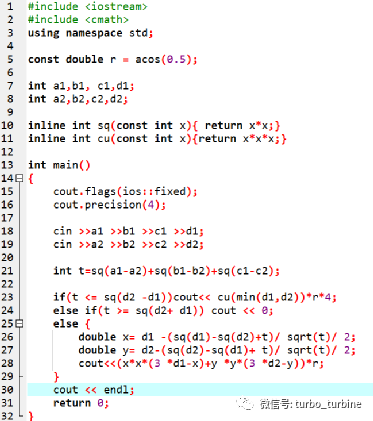
假设输入的所有数的绝对值都不超过1000，完成下面的判断题和单选题和判断题：

【解析】首先先看一下程序，通过求 t可以猜出这是三维坐标系。还有 r 可以大致猜测是球。

因为 cos60^∘=0.5 ，而 60^∘ 在弧度制下就是 π/3 。

可以猜测一下，因为 V=4/3πr3 ， r 是 π/3 ，所以本题和球关系很大，而 d 是半径。

16. 将第 21行中t的类型声明从int改为double，不会影响程序运行的结果。（）

【解析】没有任何下取整的操作，并且结果也是 double 不影响,故判对。

17.将第 26、27 行中的/sqrt(t)/ 2替换为/ 2 / sqrt(t)，不会影响程序运行的结果。（ ）

【解析】这里 sqrt 是小数，若先除以 2 会默认下取整。故判错。

18.将第 28 行中的x * x改成sq(x)、y * y改成sq(y) ，不会影响程序运行的结果。（ ）

【解析】sq() 函数内是算 int 类型的平方，这里的 x 和 y 都是 double 类型。故判错。

19.（2 分）当输入为0 0 0 1 1 0 0 1时，输出为1.3090。（ ）

【解析】手动模拟，这个不会难算。结果为 5π/12 估算一下，差不多,故判对。

20.当输入为1 1 1 1 1 1 1 2时，输出为（ ）。

A. 3.1416 B. 6.2832   C. 4.7124   D. 4.1888

【解析】走特判，所以 4/3πr3 直接带进去，其中 r 取 1  。

21.（2.5 分）这段代码的含义为（ ）。

A. 求圆的面积并 B. 求球的体积并

C. 求球的体积交 D. 求椭球的体积并

【解析】根据上面的分析和特判的 min ，所以判断是交 。

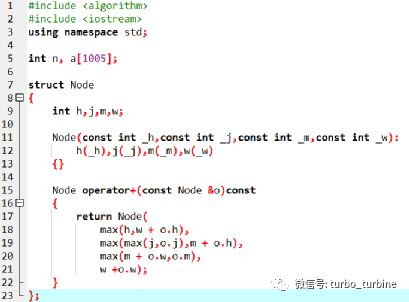
【解析】这是一段求最大子段和的程序。

22.程序总是会正常执行并输出两行两个相等的数。（ ）

【解析】这个没啥问题，正确。

23.第 28 行与第 38 行分别有可能执行两次及以上。（ ）

【解析】考虑二分到最边界，此时 (n,n+1) 会分成 (n,n) 和 (n+1,n+1) ,相等情况被特判走了，所以不会走那两行特判。若开头输入的 n<0，也只会分别执行一次。故判错。

24.当输入为5 -10 11 -9 5 -7时，输出的第二行为“7”。（ ）

【解析】n=5,所以这一段的最大字段和为 11 ,故判错。

25.solve1(1, n) 的时间复杂度为（ ）。

A. O(logn)   B. O(n) C. O(nlogn) D. O(n!)

【解析】T(n)=2T(n/2)+1T(n)=2n−1  。

26.solve2(1, n) 的时间复杂度为（ ）。

A. O(logn) B. O(n) C. O(nlogn) D. O(n!)

【解析】T(n)=2T(n/2)+nO(nlogn)  。

27.当输入为10 -3 2 10 0 -8 9 -4 -5 9 4时，输出的第一行为（ ）。

A. 13 B. 17 C. 24 D. 12

【解析】n=10,所以最大字段和为 2 10 0 -8 9 -4 -5 9 4 ，为 17。

(3)

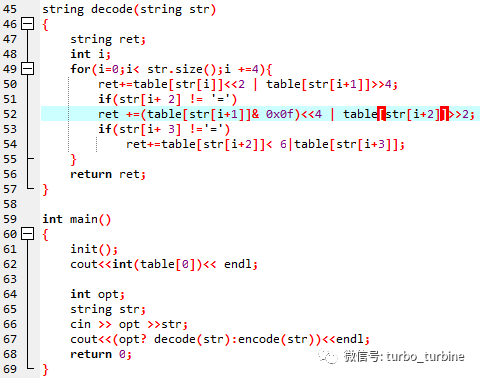
【解析】根据函数名decode和encode以及程序的描述，能比较清晰地发现这是一个加密和解密的过程。

28.程序总是先输出一行一个整数，再输出一行一个字符串。（ ）

【解析】错误，因为有可能被解码成换行符’\n’而导致换行

29.对于任意不含空白字符的字符串 str1，先执行程序输入0 str1，得到输出的第二行记为 str2；再执行程序输入1 str2，输出的第二行必为 str1。（ ）

【解析】因为是加密和解密，这两个必然相同。故判对。

30.当输入为1 SGVsbG93b3JsZA==时，输出的第二行为HelloWorld。（ ）

【解析】手动模拟,判错。

31.设输入字符串长度为 n，encode 函数的时间复杂度为（ ）。

A. Θ,O(n)B. O(n) C. O(nlogn)D. O(n!)

【解析】看程序，是 O(n) 的 。

32.输出的第一行为（ ）。

A. 0xff  B. 255 C. 0xFF  D. -1

【解析】因为table数组的类型被定义为char, 所以结果是-1而不是0xff或者 255 。

33.（4 分）当输入为0 CSP2021csp时，输出的第二行为（ ）。

A. Q1NQMjAyMWNzcAv=    B. Q1NQMjAyMGNzcA==

C. Q1NQMjAyMGNzcAv=    D. Q1NQMjAyMWNzcA==

【解析】模拟一下程序运行情况 。

三、完善程序（单选题，每小题3分，共计30分）

(1)（魔法数字）小 H 的魔法数字是 4 。给定 n ，他希望用若干个 4 进行若干次加法、减法和整除运算得到 n 。但由于小 H 计算能力有限，计算过程中只能出现不超过 M=10000的正整数。求至少可能用到多少个 4 。例如，当 n=2时，有 2=(4+4)/4，用到了 3 个 4，是最优方案。

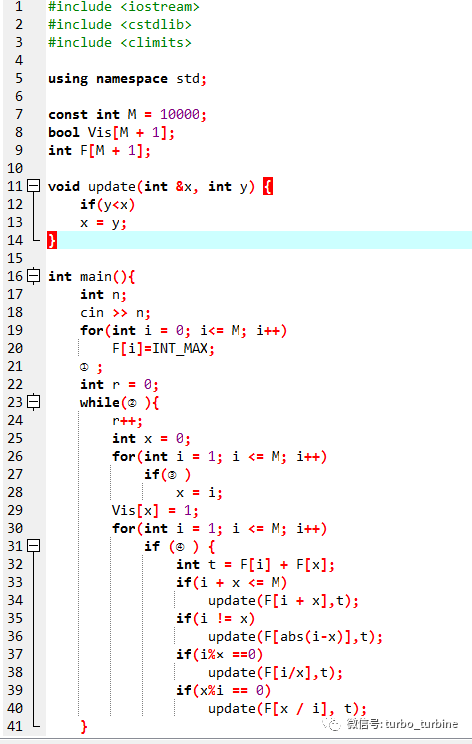
试补全程序。

本题类似 dijkstra ，每次选择已经确定最小操作的数字来转移到其他数字。

而 vis 记录已经确定不会再更改操作数的数。

0.①处应填（ ）

A. F[4] = 0 B. F[1] = 4 C. F[1] = 2 D. F[4] = 1

【解析】首先 4 需要的操作数是 1 ，1 需要的是 2 。对于程序来说，都是小操作数转移到大操作数。

0.②处应填（ ）

A. !Vis[n]            B. r < n

C. F[M] == INT_MAX   D. F[n] == INT_MAX

【解析】结束掉件首先肯定是 n已经算出来了。但 r 似乎对本题没有任何影响……

当 Fn有值时也不一定是最优的，只有当 Fn作为可以去转移别人的时候才是最优的。

0.③处应填（ ）

A. F[i] == r    B. !Vis[i] && F[i] == r

C. F[i] < F[x]  D. !Vis[i] && F[i] < F[x]

【解析】这题真的很像dijkstra，选择一个没转移过的但又不会再被转移的数。

0.④处应填（ ）

A. F[i] < F[x]  B. F[i] <= r   C. Vis[i]   D. i <= x

【解析】两个数转移到新的数，只有当这两个数都是最优的时候，才能保证本次转移不会白转移（指其中一个数再更新本次转移作废）。

(2)（RMQ 区间最值问题）给定序列 a1,...,an和 m 次询问，每次询问给定 l,r，求 max{a1,...,an} 。

为了解决该问题，有一个算法叫 the Method of Four Russians ，其时间复杂度为 O(n+m) ，步骤如下：

建立 Cartesian（笛卡尔）树，将问题转化为树上的 LCA（最近公共祖先）问题。

对于 LCA 问题，可以考虑其 Euler 序（即按照 DFS 过程，经过所有点，环游回根的序列），即求 Euler 序列上两点间一个新的 RMQ 问题。

注意新的问题为 ±1 RMQ，即相邻两点的深度差一定为 1 。

下面解决这个 ±1 RMQ 问题，“序列”指 Euler 序列：

设 t 为 Euler 序列长度。取 b=⌈log2t/2⌉。将序列每 b 个分为一大块， 使用 ST 表（倍增表）处理大块间的 RMQ 问题，复杂度 O(t/blogt)=O(n) 。

（重点）对于一个块内的 RMQ 问题，也需要 O(1) 的算法。由于差分数组 2^b−1 种，可以预处理出所有情况下的最值位置，预处理复杂度 O(b2^b)，不超过O(n) 。

最终，对于一个查询，可以转化为中间整的大块的RMQ问题，以及两端块内的 RMQ 问题。

试补全程序。

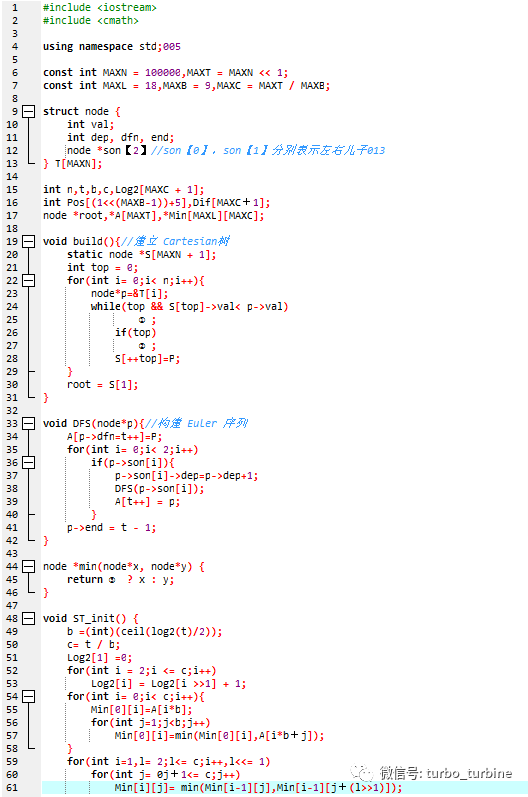
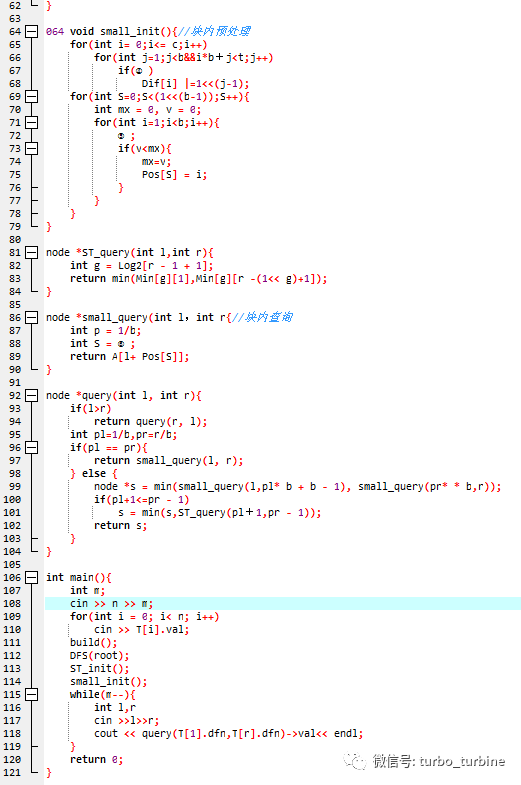
38.①处应填（ ）

A. p->son[0] = S[top--]   B. p->son[1] = S[top--]

C. S[top--]->son[0] = p   D. S[top--]->son[1] = p

【解析】这部分是在建笛卡尔树，笛卡尔树就是对于序列区间 (l,r) ，选取最大值 x 做为这区间的根，然后再跑 (l,x−1) 和 (x+1,r) ，再和这两个区间的根连边。可以用单调栈来解决。对于栈顶小于当前元素的情况，显然可以不断弹出，使当前元素找到他最大的左二子。

39.②处应填（ ）

A. p->son[0] = S[top]   B. p->son[1] = S[top]

C. S[top]->son[0] = p   D. S[top]->son[1] = p

【解析】而上述操作结束后，栈顶的元素就比当前元素大，所以可以先把栈顶的右儿子设为当前元素。若后面出现更大的也会覆盖掉。

40.③处应填（ ）

A. x->dep < y->dep B. x < y

C. x->dep > y->dep    D. x->val < y->val

【解析】其实在建完笛卡尔树后，val 就没有用处了。这部分的 min 是在处理 st 的时候用的，所以是考虑深度。另外都 min 了不可能去操作 max 的方法吧。

41.④处应填（ ）

A. A[i * b + j - 1] == A[i * b + j]->son[0]

B. A[i * b + j]->val < A[i * b + j - 1]->val

C. A[i * b + j] == A[i * b + j - 1]->son[1]

D. A[i * b + j]->dep < A[i * b + j - 1]->dep

【解析】因为只有 +1 和 −1 两种情况，所以按照题目说法，这里的二进制也是表示这个，用来存储本块内的情况。

42.⑤处应填（ ）

A. v += (S >> i & 1) ? -1 : 1

B. v += (S >> i & 1) ? 1 : -1

C. v += (S >> (i - 1) & 1) ? 1 : -1

D. v += (S >> (i - 1) & 1) ? -1 : 1

【解析】这里是预处理出块内所有的 2^b−1种情况，方便到时候 O(1))算，因为刚刚是后者小于前者时为 1 。所以为 1 的时候应该 −1 ，反之 +1 。另外注意一下 i 是从 1 开始的，故

43.⑥处应填（ ）

A. (Dif[p] >> (r - p * b)) & ((1 << (r - l)) - 1)

B. Dif[p]

C. (Dif[p] >> (l - p * b)) & ((1 << (r - l)) - 1)

D. (Dif[p] >> ((p + 1) * b - r)) & ((1 << (r - l + 1)) - 1)

【解析】对于一个块内的查询 (l,r) 。这里的 S 是要确认本区间的状态。而刚刚的 Dif 已经预处理好了，p 是块的位置。