2024年“华数杯”A题各问解题思路
-
-
上海小升初 这家伙很懒，还没有设置简介
0 人点赞了该文章 · 163 浏览
2024年“华数杯”国际大学生数学建模竞赛（以下简称“竞赛”）是中国未来研究会大数据与数学模型专业委员会、 天津市未来与预测科学研究会主办的大学生学科类竞赛，竞赛由华数杯竞赛组委会负责组织，旨在提高学生运用数学解决实际问题的能力以及英文科技论文的写作能力，同时可以快速提高美国MCM/ICM竞赛参赛水平。欢迎各高等院校组织学生报名参赛。
问题一：
建立扩散数学模型，描述放射性废水在海水中扩散的速率和方向，同时考虑水体运动、环境条件和其他影响因素。
据了解，截至2023年8月27日中午12点，有1095 吨放射性废水从日本排放到海洋环境中。如果不再排放放射性废水，请预测2023年9月27日日本近海域放射性废水污染的范围和程度。
首先考虑最基本的三维扩散模型(水体运动造成的平流和扩散)，如下式所示：
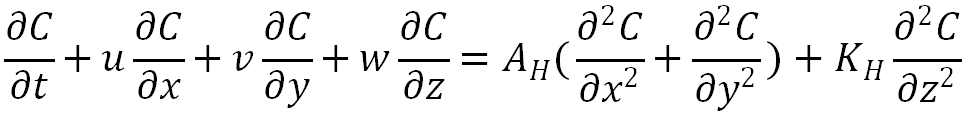
x、y和z是传统的笛卡尔坐标；u、v、w分别表示扩散的纬向速度、经向速度和垂直速度；C为浓度，单位为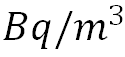
；t是时间(s)；C在三维场景下也可表示成C(x，y，z，t)，表示在某时刻特定位置的气浓度；∂c/∂x、∂c/∂y和∂c/∂z则表示不同方位的浓度梯度，
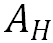和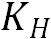
分别为氚的水平扩散系数和垂直扩散系数。
接着考虑更多的条件：自衰变和海水中悬浮物对氚吸附，这两个条件会对水中氚浓度。自衰变过程完全取决于氚的半衰期，而与悬浮材料吸收有关的清除过程可以通过采用Tsumune使用的方法来近似。
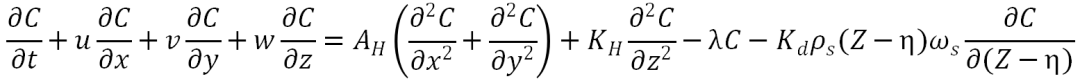
λ是氚的放射性衰变常数，约为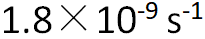
（半衰期为12.43年）；
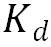为核素从水到悬浮物的分配系数，取
；
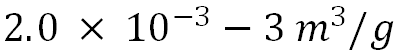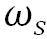为悬浮物沉降速度，设为
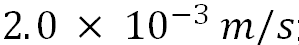；ρs(z)为表层悬浮物的浓度，约为0.25g/m3。在三维场景下，其垂直分布表示为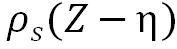
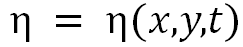为地表高程。
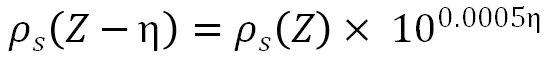
在对速度进行设定时，通过查找资料，水平速度最大一般为vmax=4.75m/s
在本文中，结合实际报道，我们将初始值设置为0.29Bq/m3，当浓度C大于0.001Bq/m3，则判定为受到了污染，至于距离结合各位的想法即可。
数据来源：The ocean surface current analysis real-time (OSCAR)
问题二：
在2023年，日本政府已经三次倾倒放射性废水。如果今后不再倾倒，请建立数学模型，研究三次倾倒后放射性废水的扩散路径。考虑到诸如海洋环流模式、水动力、海底地形、深度变化、潮汐影响和季节波动等因素。污染中国领海需要多长时间?
细读题目发现，（1）、（2）和第（4）问，核废水都是倒完一定量后，“今后不再倾倒”。我们就继续在第一问的基础上进行模型改进。
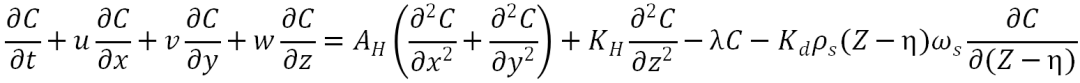
首先对海底地形进行引入。第一问考虑到深度变化，但是忽略地形。
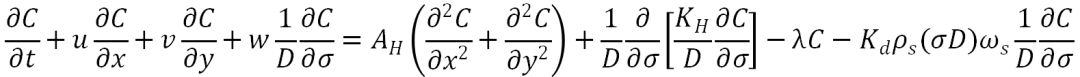
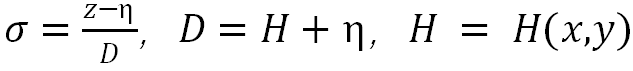为底部地形
σ的范围从z=η时的σ=0到z=-H时的σ=-1。
这是在考虑三维场景，海洋地形包括深度变化的模型。其余加入的影响因素则为海洋环流模式、潮汐影响和季节波动。
这三方面因素作用到变量上则是影响到温度和传播速度，温度也会对扩散系数进行影响。
分别表示扩散的纬向速度、经向速度和垂直速度，
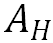和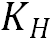
分别为氚的水平扩散系数和垂直扩散系数。
先对速度进行分析，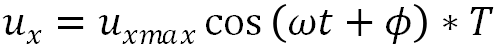
, 
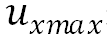表示最大纬向速度，T是温度系数，区分不同季节。这是纬向速度分析，至于经向速度同理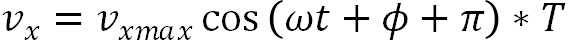
为了简化模型，本文没有考虑对于垂直速度的影响，因为侧重点在于
①传播到中国海域（水平方向）
②太平洋垂直最深度在于10KM，
而日本海域到中国海域距离远远大于此数，所以在垂直方向上的传播对于何时到达中国海域影响不大。所以在考虑洋流因素对垂直传播速度的影响可以忽略不记。按照定量处理。
T作为温度系数反映不同季节温度差异对扩散系数和传播速度的影响。
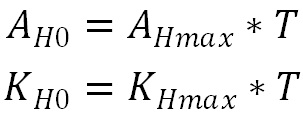
模型更新为
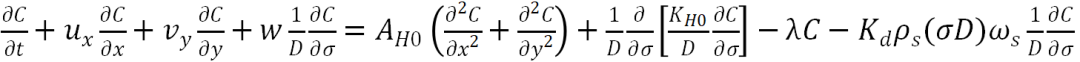
模型建立完毕之后还有一些细节带入，比如多远的距离（x，y）取何值才算是到达中国海域，浓度C大于多少算的得上污染，初始排放中氚含量是多少。
在本文中，结合实际报道，我们将初始值设置为0.29Bq/m3，当浓度C大于0.001Bq/m3，则判定为受到了污染，至于距离结合各位的想法即可。
数据来源：The ocean surface current analysis real-time (OSCAR)
问题三：
日本政府宣布倾倒放射性废水后，有关部门对1万名中国居民进行了调查。包括他们是否会在放射性废水倾倒前后购买和食用海鲜。结果如表1所示。根据表1的调查结果，分析放射性废水倾倒对中国未来渔业经济的长期影响。
由于曾经不吃海鲜的人数与日本排放核废水后不吃海鲜的人变化不大，故而我们可以暂不考虑曾经不吃海鲜的人，对于曾经吃海鲜的人，曾经8675个吃海鲜的人其中有6437个人放弃食用。可以使用该组数据模拟废水排放对于渔业的影响。
首先，我们可以使用2010-2022年间的渔业经济指标预测未排放核废水情况下的未来的渔业发展情况，通过回归，或灰色预测模型得到相应结论，
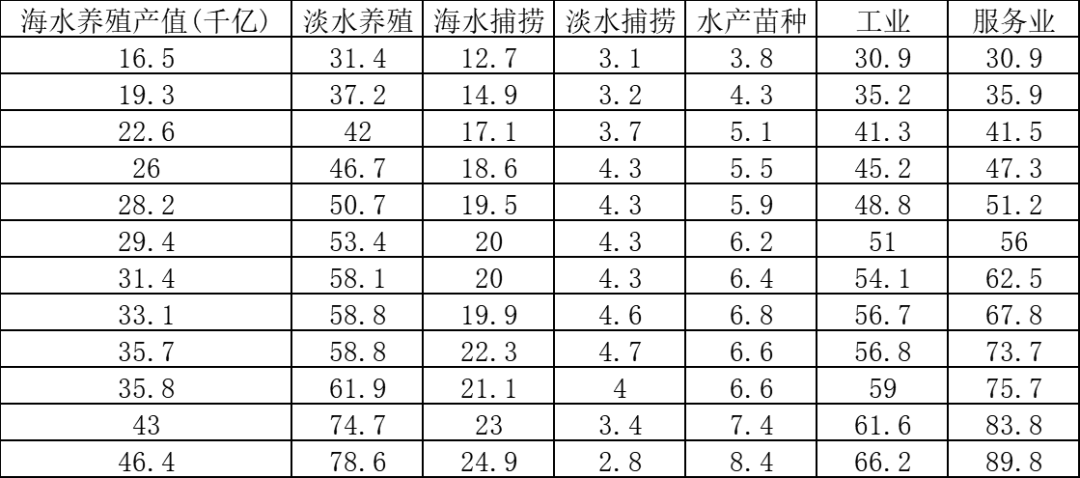
GM(1,1)预测未来五年(无排放)
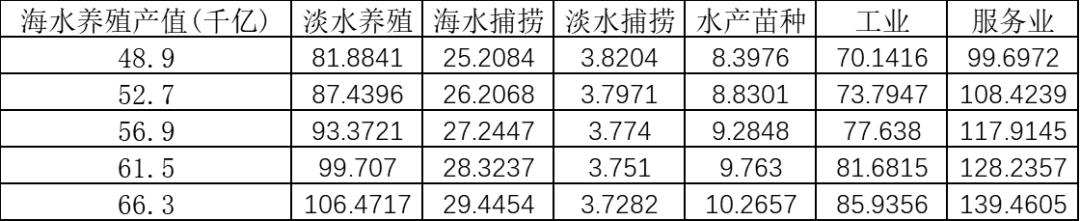
由于渔业经济主要由渔业/渔业工业/渔业服务业组成，考虑到日本排放废水短期主要影响海鲜销售，故主要考虑对于海鲜养殖与捕捞业的影响。
P(E)表示继续食用海鲜人群比例，约为0.259。假设未来第y年海水养殖业及捕捞产值(未排放)为Y1(t)=4638.84亿元及Y2(t)=2488.9亿元，那么第t年排污后的海水渔业产值S(t)可以估计为：
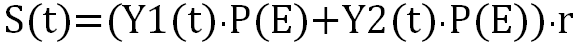
其中渔业服务业及渔业工业以及淡水渔业产值短期内影响如若不计，则未来渔业经济产值估计为：(排污后的海水渔业产值+淡水渔业产值+渔业工业+渔业服务业)×往年同期增数
GM(1,1)预测未来五年(有排放)
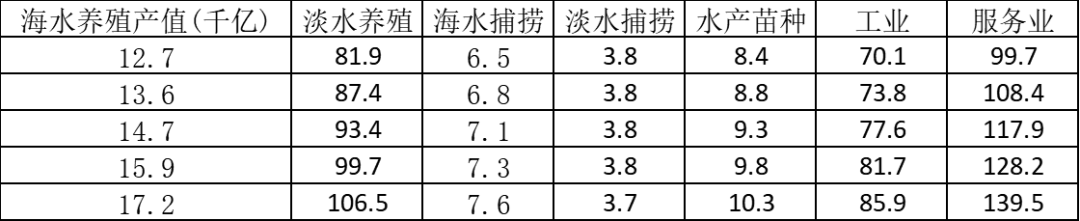
(数据来源:全国渔业经济统计公报 (moa.gov.cn))
问题四：
日本排放放射性废水30年后，请判断世界上所有的海洋是否都会被污染。哪一年才会被彻底污染?其中，哪个地方污染最严重?
这个相当于模型上没有太多改变，因为在初始第一问，模型已经考虑到了半衰期，第一问实际计算中半衰期可以忽略影响，但是在第四问中，30年的时间跨度半衰期影响则大大加重。
不同地区海洋深度大不相同，那需要考虑到垂直情况吗，答案是否定的。
海洋在水平方向的尺度远大于垂直方向，因此需要划分大量高精度网格进行合理的三维模拟，计算量相当大。其次在，这种划分是不必要的，因为污染物在垂直方向上的分布是近似均匀的。
结论来源：Yi Liu, Xue-Qing Guo, Sun-Wei Li, Jian-Min Zhang, Zhen-Zhong Hu, Discharge of treated Fukushima nuclear accident contaminated water: macroscopic and microscopic simulations, National Science Review, Volume 9, Issue 1, January 2022, nwab209, https://doi.org/10.1093/nsr/nwab209
则第四问就是在已知时间的情况下求解浓度分布，重点考虑半衰期。
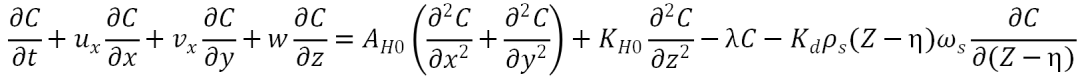
备注：第一问的模型就已经是三维+垂直因素考虑+半衰期，较为完善，所以在后续对于模型的完善较少，加入了季风洋流因素，如果想层层递进式，可以在第一问把垂直相关的式子删除，半衰期删除。则为：
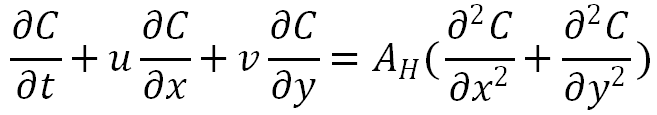
全部 0条评论