【第一题】如图, 将一个正方形硬纸片的四个角分别剪去一个等腰直角三角形, 最后剩下一个长方形. 正方形边长和三角形直角边长都是整数. 若剪去部分的总面积为 40 平方厘米, 则长方形的面积是多少平方厘米.

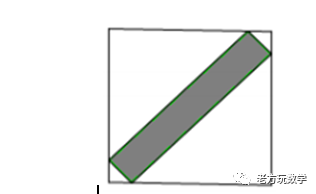
这是今年的华罗庚杯赛的几何题目，已知正方形硬纸片的四个角分别剪去一个等腰直角三角形, 最后剩下一个长方形. 正方形边长和三角形 直角边长都是整数. 若剪去部分的总面积为 40 平方厘米,要求长方形阴影面积是多少。

【第二题】如右图所示, 两个边长为 6 的正方形 ABFE 和 CDEF 拼成长方形 ABCD. G 为 DE 的中点. 连接 BG 交 EF 于 H . 求图中五边形 CDGHF 的面积.

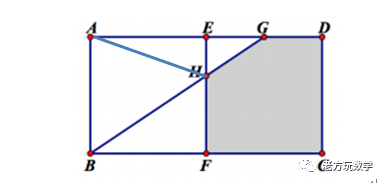
将AH连接起来，三角形ABH是正方形ABFE的一半：

                   三角形ABH=18

      三角形ABG的面积=6*9/2=27

  所以：

      三角形AHG的面积=9

      又AE=2倍EG

所以

三角形AEH的面积是三角形EHG的2倍

得到三角形EHG=3

阴影面积=正方形CDEF面积-三角形EHG面积=36=33