华罗庚金杯第三届决赛（一试）试题

1、计算：1/3+1/15+1/35+1/63+1/99

2、说明360的约数有多少个？这些约数的和是多少？

3、观察数表（横排为行，竖排为列），根据前5行所表达的规律，说明1991/1949这个数位于第几行第几列？

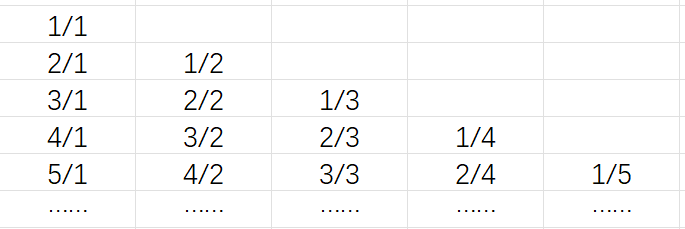
4、将一个圆形纸片用直线划分为大小不限的若干小纸片，如果要分成不少于50个小纸片，至少要画多少条直线？

5、某校下午2点派车去工厂接一名劳模来校作报告，往返需要1小时。已知劳模在下午1点从工厂出发，步行前往该校，途中遇到接他的汽车，上车后汽车驶向学校，于下午2点40分到达学校。问：汽车速度是劳模步行速度的多少倍？

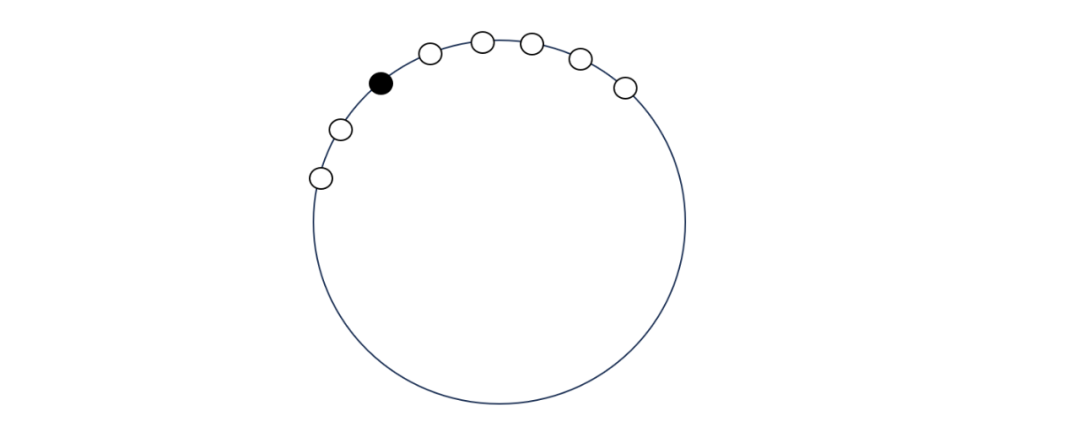
6、一个圆周上放了一枚黑色棋子和1990枚白色棋子。一名同学进行这样的操作：从黑色棋子开始，按顺时针方向，每隔一枚取走一枚，当他取到黑子时，圆周上还剩多少白色棋子？

试题解答：

1、计算：1/3+1/15+1/35+1/63+1/99

考察分数裂项。

原式=1/2（1-1/3+1/3-1/5+1/5-1/7+1/7-1/9+

1/9-1/11)=1/2*10/11=5/11

2、说明360的约数有多少个？这些约数的和是多少？

考察约数个数和约数和定理。

将360分解质因数=2*2*2*3*3*5（2^3*3^2*5）

约数个数=（3+1）*（2+1）*（1+1）=24

约数和=（1+2+4+8）*（1+3+9）*（1+5）=1170

3、观察数表（横排为行，竖排为列），根据前5行所表达的规律，说明1991/1949这个数位于第几行第几列？

考察递推数列。

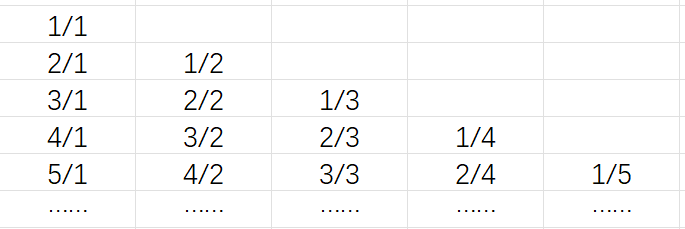
通过数列可观察，数列每行分子和分母的和相等，且等于行数+1，所以1991/1949在（1991+1949-1）=3939行；

同样，通过数列观察，分母即为列数。

综上，1991/1949在3939行和1949列。

4、将一个圆形纸片用直线划分为大小不限的若干小纸片，如果要分成不少于50个小纸片，至少要画多少条直线？

考察递推数列。

初始1张小纸片，知：每画一条直线，最多可增加n个小纸片，转化为等差数列求和问题。

知：1-9的和为45，即画9条直线最多仅有（45+1）=46个小纸片，而1-10的和为55，至少要画10条直线。

5、某校下午2点派车去工厂接一名劳模来校作报告，往返需要1小时。已知劳模在下午1点从工厂出发，步行前往该校，途中遇到接他的汽车，上车后汽车驶向学校，于下午2点40分到达学校。问：汽车速度是劳模步行速度的多少倍。

考察相遇问题。

可以通过劳模和汽车行驶相同行程的时间比，得出速度比。

通过汽车2点出发，2点40分到校，知：汽车单程行驶20分钟。而原计划接劳模往返1小时，单程需要30分钟。

汽车与劳模相遇时间为2点20分。劳模1点出发，80分钟所走路程为汽车10分钟所走路程，时间比8:1，速度比1:8。即，汽车速度是劳模步行速度的8倍。

6、一个圆周上放了一枚黑色棋子和1990枚白色棋子。一名同学进行这样的操作：从黑色棋子开始，按顺时针方向，每隔一枚取走一枚，当他取到黑子时，圆周上还剩多少白色棋子？

题目看似复杂，但把每一圈单独做分析即可。

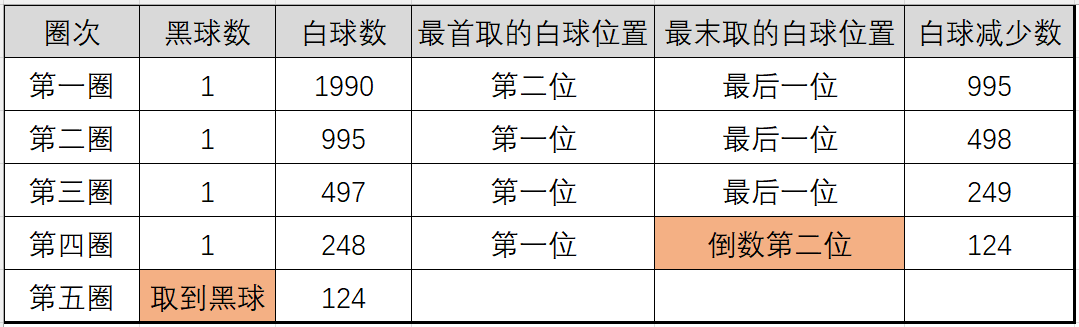
当取到黑子时，圆周上还剩124颗白色棋子。