【行远讲堂】数字谜中的多位数恒等式——从上周一道华杯题说起
华杯数字谜的两种不同思路
这次华杯解答题中的数字谜题目如下:(非常感谢沃伦教育黄达鹏老师提供的准确试题)

广东是竞赛大省,这两天我陆续看到了广州本地机构关于这次好几种不同版本的解析。大部分问题的解法大家都大同小异。和我之前帖子里解法有比较明显不同的,一道是几何题,更广泛的做法是补全成大三角形用等高和鸟头去做,比我用定比分点的做法步骤麻烦一些,但相对有更多小学生学过。
另一道便是这道数字谜。
我所看到的所有其他解析,都是采用的“从特殊到一般”的做法。由于910分解成两个两位数相乘只有2种形式,可以先考虑k=1的特殊情形,把四种情况分别枚举找到唯一的特殊解,再证明其对一般情况成立。
这里引用广州某本地机构的解析(出处不是很明,故保留原解析水印,方便家长查证):
备注:这个解析漏了一个13×70的情况,但也容易排除

这应该也是小学生解这道题可能能想到的一种思路了。
而我在上一篇解析里给了一个与之相反的思路:从一般到特殊。
这是一个相对比较偏中学的思路:
如果一个恒等式对所有的k均成立,则所有和k有关的项,其系数和一定为0。
鉴于写完之后有不少家长来问,我把这个解析在这里补充详细一些:

而类似这样的“数字谜恒等式”,历年来还有一些比较经典的考题,下面一起来看一看。
这些题目的共同点是:解题过程中会出现形如aa...a形的多位数,而我们可以利用下面的几组关系式进行变形:
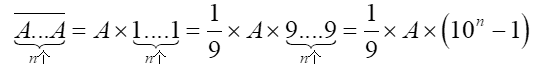
想要解决这类问题,熟练掌握上面的结构变形是非常重要的。
四年级导引《多位数与小数》超越篇第7题
四年级高思导引有一道很著名的超纲难题,出现在第13讲的超越7:

原版导引的解析文字采用的也是一种“找规律”的方法,利用从特殊到一般的方法得到答案,全文如下:

解析本身没有问题,但孩子首先不容易想到从简单情况分析,其次68和668的平方本身不是常见平方数,四年级孩子也很难有能力一眼看出平方根。至于后面的证明显然是超出孩子证明能力的。
我在去年参与修订新版高思导引的时候,也给出了一个“从一般到特殊”的证明思路,利用位值原理与配方,大致如下:
(原式)
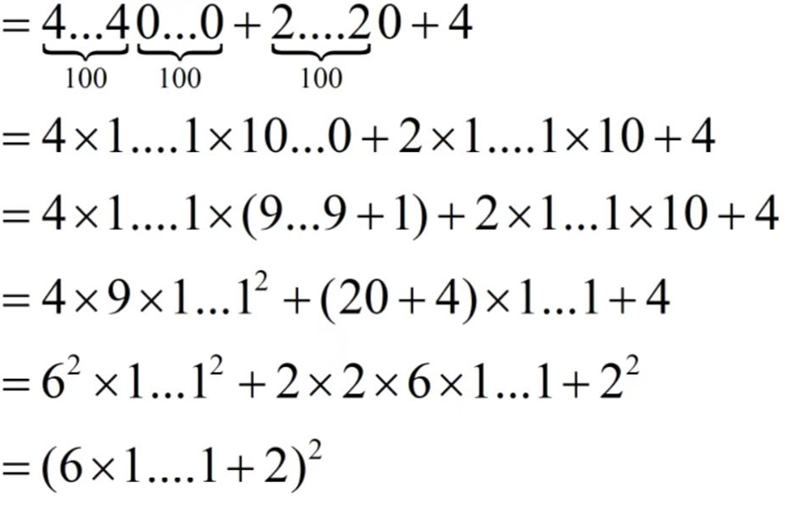
可以发现,一正一反的两种思路,和华杯这道题是相似的。
2022年华数之星广州夏令营第7题
类似的多位数恒等式,去年的华杯中也有考察:

由于不存在缩小范围的条件,同时还需要求出所有的解,这道题实际上的难度可能还高于今年这道。
不过总归都属于小学生很难做全对的问题。
解析思路如下,同样是利用位值拆分。但这里可以直接约去含k的式子简化计算,就不涉及到恒等式相关的知识了:

2019年AMC12第22题
把目光放远一点,在“美国高联初试”AMC12中,同样有类似“数字谜恒等式”的问题出现,和前面的问题也具有相似性:
原题是英文,这里就只放中文版了:

这道题的变形思路和上面几题稍微有些不同,解析如下:

可见,类似多位数结构的位值拆分及分析,即使放到中学竞赛也是可能出现的考点。
碎碎念了这么多,只是希望同学们能够对于这类问题有一个更系统的认识,能够熟练运用前文提到的变形方法,并以此为基础更好的掌握特殊结构多位数类的计算分析问题。




全部 0条评论