最近，那个号称小奥“天花板”的赛事“华杯”，比了寒假的第一场：文化营。

当天晚上，各大机构的回忆版真题、解析已经在各大家长群反复流传了。

看了很多机构、老师的专业分析，作为一个“自鸡”为主的家长，我决定从考生和家长的视角，提供一种不同的解读，以及对未来的备考总结出一些启示和建议。

关于“基本功”

这次考试，再一次验证了我之前反复强调的“基本功”的重要性。（见《基本功真的对考试提分有大帮助吗？》）

所谓基本功，就是到了高中、大学都要用到的东西，比如计算能力。

本次第一题：

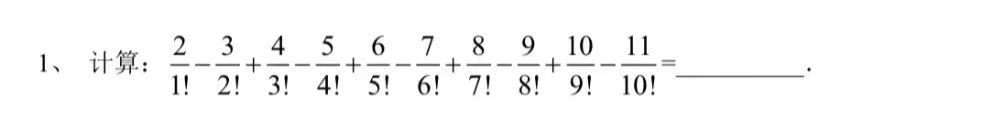
全卷开篇第一道，考核计算。

就算考生想不出“简便技巧”和“诀窍”，只有10项，计算扎实的话硬算也是能硬算出答案的。

又比如二试，解答题的第一题：

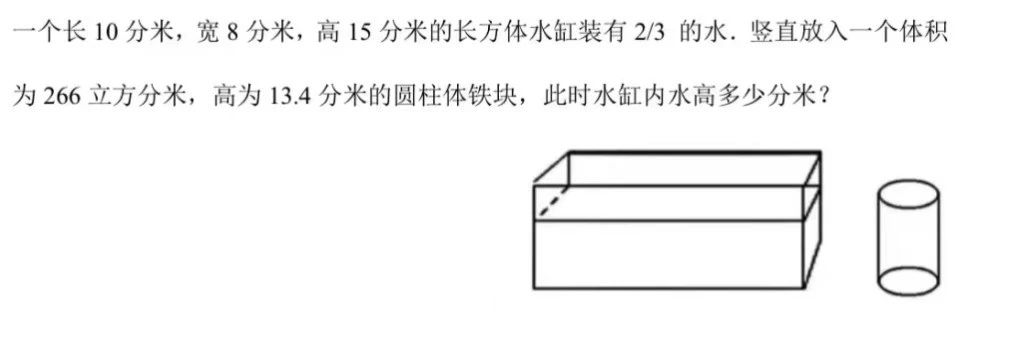
挺简单的一道题，思路一点都不难，甚至很多没学过奥数的孩子都能想出解答方法。

但这题难就难在计算比较麻烦，或者说，计算过程有点“恶心”。

再比如，全卷难度极高的一道解答题：

这一道解答题，就算不是全卷最难，也肯定是最难之一了。

这道题难就难在于：

那个“佩尔方程”列出来之后，除了纯枚举之外没有什么巧妙方法。

我看了各机构各老师都一样，都只能暴力硬算，反复尝试。

虽然尝试的过程中可以利用余数特征稍微排除一些，但硬算无法避免。

可见，不管是全卷第一题，还是二试中最简单或最难的解答题，大量、繁复的计算无法避免。

在有限的时间内，扎实的计算基本功，非常、非常重要。

关于超纲和“中学化”

我之前在文章中也说过，小奥两大天花板赛事各有特点：

迎春杯“不超纲”，尽管在小学范围内，但题目灵活、创新；

华杯赛常“超纲”，近年来“中学化”越演愈烈。

这次中学化也是鲜明的特色，比如：

这道题对小学生真的不容易。

配方之后变形平方差，典型的初中思路，初中因式分解的常用方法。

又比如：

立体几何，用上欧拉公式，在过去华杯赛中也算是不常见的考点。

这已经有点不是初中化了，我记得我当年是高中才学的，能算“高中化”么？

关于“押题”

每次一考完，很多机构就会马上“回顾”总结：

哪道真题在我们讲义上有类似的；

哪道题在我们在什么时候的课上讲过……

说白了，就是想说我们“押题”很准。

其实，除非考前两天刚好讲过类似的，“押题”对大部分孩子来说用处并不大。

一个机构一年下来讲过的题成百上千，底层的模型来来去去就是那些，授课中讲过类似的题目很正常。

但有多少个孩子能只要讲过就记住的？

如果“讲过”都能理解、记住，这样的孩子本身靠实力已经能远超一等奖分数线了，根本不用靠押题。

面对“押题”，这套题本来就很“反常”、“反套路”：

你什么时候见过任何一份小奥杯赛的考卷（不管真题还是模拟题），没有考任何的“计数”内容？

且也没有考行程？

你什么时候你见过往死里反复考最难的数论？

这次不但数论占比大，而且都是比较偏代数的数论（中学化）。

一般我们想象中比较正常的试卷大概是长这样：

每个模块都有考核，有重点、有侧重，整体比较均衡。

但这是选拔性的竞技比赛，出题人就是要“反常规”：

“不定方程”我不但要考，还有在分数高的解答题里都反复考（下图）；

数论题更是一题接一题；

计算量非常大，而且数字“很难看”，很多孩子一边算一边“怀疑人生”……

关于长期备考的建议

综上，这次的题考试范围很“反常”。

从思维难度看，不算难；

但计算量很大，非常大；

因此从体感上，很难，甚至越做越“恶心”。

给一点长期备考的建议：

一是基本功还是要扎实，特别是计算能力。

在限时的考场上，什么状况都会发生，发挥很可能打折扣，唯一能应对的就是平时练好基础功。

二是认真、扎实学好每一个模块和内容。

不要猜测什么会考、什么重点考、什么不考，就算是老师的猜测也可能没太大指导意义。

三是什么押题班、冲刺班并不那么重要，重点是以前系统学过的、机构长期班老师讲过的题目能理解、吃透。

四是适应变化，面对出题“中学化”、范围“反套路”，只能接受，扎扎实实地多学一些、拓宽知识面。

华杯小高组本来就面向小学高年级的头部尖子，作为领跑者，多学一点初中的内容也是应有之义。

五是多参加比赛，以赛代练去积累临场经验，锻炼心态。

有孩子看到解答题的那道平面几何，那个图跟去年暑假的一模一样，就觉得是老题，能搞掂，于是马上先做那一道（见下图）。

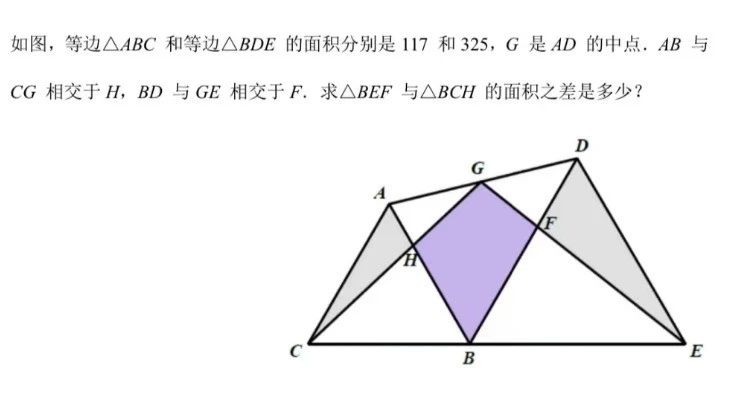
其实尽管图是一样的，但问法和解法都不同。

孩子一直都做不出来，觉得连老题都对付不了，于是心态就崩了。

又比如有孩子列出了“佩尔”方程，一直试不出答案，总觉得答案就在眼前，结果浪费了大量的时间。

其实不是数感和运算能力很强的孩子，佩尔方程完全可以战略放弃。

六是不要过度追求技巧和诀窍，不要浮躁，踏实做题。

这次华杯的思维难度一般，但普遍“体感”较差，反映出大部分人基础不扎实，思考浮躁。

做题不要追求数量，慢就是快。

越是反常诡异的卷子，越能反映出孩子的弱项。

只要吸取教训，总结经验，着眼长期，就一定会越来越好。

一起努力！