
(2015年第二届鹏城杯,五、六年级的数学试题大部分一样,合并列出,差异在文中标注。)一、填空题(满分60分,每小题6分)
1、不同的数字A、B、C、D,使得等式AAAA+BBB+CC-D成立,则A+B/C×D=?
2、如图所示,三角形ABE是边长为21的正三角形,四边形BCDE的周长是三角形周长的两倍,则五边形ABCDE的周长=?
3-1(五年级)计算:2015×20162016-2016×20152015=?3-2(六年级)计算:20152016×20162015-20152015×20162016=?
4、将[3.95]/7化为小数,小数点后第2015位的数字是几?其中[3.95]表示不超过3.95的最大整数。
5-1(五年级/六年级第9题)处在A点的狗追赶与A点距离30米的B点的狐狸,狗一步跑2米,狐狸一步跑1米,狗跑2步的时间狐狸跑3步,问:当狗赶上狐狸时与A点的距离等于多少米?5-2(六年级)一件工作,甲、乙两人合作8天完成,乙、丙两人合作6天完成,甲、丙两人合作12天完成,若甲、乙、丙三人合作,需要几天完成?
6、非零自然数a、b的最大公因数和最小公倍数之和恰等于a、b的乘积,则(a²b²/a²+b²)^10=?
7-1(五年级)一个长方体,不同单个面的面积与其周长的比分别为3、6、8,则长方体体积与表面积的比为?
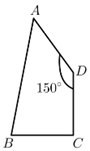
7-2(六年级)如图,四边形ABCD中,AD=CD=BC,∠C=90°,∠D=150°,则∠ABC=?
8、设a、b、c、d是1-9之间的四个不同数字,用这四个数字(不能重复)可以组成很多不同的四位数,小明把所有可能组成的四位数加起来,但他不小心把其中一个四位数多加了一遍,结果为128313,那么,正确的结果应该是?
9(五年级)在任意n个正整数里,必有两个数,它们之和或差能被50整除,最小的正整数n为?
10、棱长为1的正方体的6个面分别标有不同的点数,下图是从不同角度观察同一个正方体的四种情形,若将10个完全相同的正方体粘合成一个1×1×10的长方体,则长方体表面标记的点数和的最大值是?二、解答题(满分60分,11-13题各10分,14/15题各15分)
11-1(五年级)计算:1/7×(13.21×77/25-3.75÷19/21)+(15/4÷19/41+13.46×14/25)11-2(六年级)计算:1/4×(4.85÷5/18-3.6+6.15×18/5)+[5.5-1.75×(5/3+19/21)]
12、某校学生志愿者社团成员的五分之一安排做交通协管员,有52名成员在医院做义工,还有若干个学雷锋小组派到各社区服务,每个小组都由社团的七分之一成员组成,问该学生志愿者社团共有成员多少人?
13、如图,直角梯形ABCD,AD∥BC,∠BAD=90°,AD=AB=2BC=2,连接对角线AC、BD交于O,求图中阴影部分面积。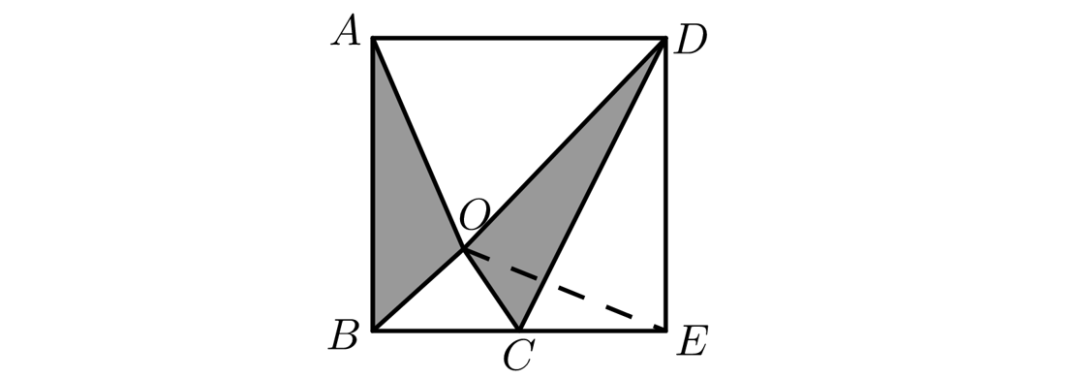
14-1(五年级)把1到70的所有自然数平均分为两组,将每组的35个数乘起来求积,然后将所得的两个积相加,所得和数称为一个“鹏程数”。证明下面两小题:
(2)若一个“鹏程数”不是2的倍数,则这个“鹏程数”是2015的倍数。14-2(六年级)具有以下性质的自然数叫“鹏程数”:(1)在它的各个数位上,除数字0外,数字1-9都出现过,(2)任何相邻的两个数位上的数字所组成的两位数都是17或23的倍数,例如:923468517就是一个9位的鹏程数,试证明2015位的“鹏程数”必定是合数。
15、证明下面两小题。
(1) 试证明:直线上存在4个点,使得这4个点两两之间的个距离恰为1、2、3、4、5、6这六个值;
(2) 在直线上是否存在5个点,使得这个点两两之间的个距离恰为1、2、3、4、5、6、7、8、9、10这十个值?如果存在,请举一例:如果不存在,请说明理由。一、填空题(满分60分,每小题6分)
1、不同的数字A、B、C、D,使得等式AAAA+BBB+CC-D=2015成立,则A+B/C×D=?
数字谜题,与2014年第2题相似。观察,等式结果的最高位为2,百位是0,可知,A=1,即BBB+CC-D=2015-1111=904,同理,结果最高位为9,十位为0,可知,B=8,即CC-D=904-888=16,因十位为1,个位要向前进位,得C=2,D=6。
2、如图所示,三角形ABE是边长为21的正三角形,四边形BCDE的周长是三角形周长的两倍,则五边形ABCDE的周长=?
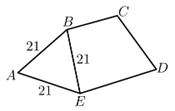
四边形周长是三角形周长的两倍,可知,BC+CD+DE=21×3×2-21=105,五边形ABCDE的周长=BC+CD+DE+AB+AE=105+21+21=147。
3-1(五年级)计算:2015×20162016-2016×20152015=?原式=2015×2016×10001-2016×2015×10001=03-2(六年级)计算:20152016×20162015-20152015×20162016=?
原式=(20152015+1)×20162015-20152015×(20162015+1)
=20152015×20162015+20162015-20152015×20162015-20152015=10000。4、将[3.95]/7化为小数,小数点后第2015位的数字是几?,其中[3.95]表示不超过3.95的最大整数。
[3.95]/7=3/7=0.428571428571……每6位一个循环。2015除以6余5,小数点后第2015位的数字是7。5-1(五年级/六年级第9题)处在A点的狗追赶与A点距离30米的B点的狐狸,狗一步跑2米,狐狸一步跑1米,狗跑2步的时间狐狸跑3步,问:当狗赶上狐狸时与A点的距离等于多少米?应用题的核心是找到相等量,这题可以设狗跑2步的时间和狐狸跑3步的时间为单位时间。那么每个单位时间里狗跑了2×2=4米,狐狸跑了3×1=3米,即每个单位时间狗可以追上狐狸1米,要追上狐狸,需要30个单位时间,期间狗共跑了30×4=120米。
5-2(六年级)一件工作,甲、乙两人合作8天完成,乙、丙两人合作6天完成,甲、丙两人合作12天完成,若甲、乙、丙三人合作,需要几天完成?
设甲、乙、丙单独工作分别需要x、y、z天完成,1/x+1/y=1/8,1/y+1/z=1/6,1/x+1/z=1/12。
1/x+1/y+1/z=(1/8+1/6+1/12)/2=3/16,三人合作16/3天完成。6、非零自然数a、b的最大公因数和最小公倍数之和恰等于a、b的乘积,则(a²b²/a²+b²)^10=?
碰到这种带n次方的除法,我们首先应该有个大致判断:a、b肯定是在0、正负1、2、3这几个数。然后我们尝试推导。
方法一:我们可以把a、b写成nA和nB,那么:最大公因数就是n,最小公倍数就是nAB。根据题意有等式:n+nAB=ab=n²AB,即1+AB=nAB,AB(n-1)=1。因为A、B、n都是自然数,仅有A=B=1、n=2时等式成立。即a=b=2。代入后得答案为1024。
方法二:设(a,b)=x,[a,b]=y,xy=ab,根据题意得x+y=xy,x=y=2。得a=b=2。代入后得答案为1024。
7-1(五年级)一个长方体,不同单个面的面积与其周长的比分别为3、6、8,则长方体体积与表面积的比为?
ab/2(a+b)=3(1)、ac/2(a+c)=6(2)、bc/2(b+c)=8(3)。这是已知信息。题目要求我们求的结论我们也写个式子就是abc/2(ab+ca+bc)。这时候就可以找到联系并向结论靠近。我们把(1)式分子分母均乘以c得:abc/2ac+2bc=3,(2)(3)式用类似方法可得abc/2ab+abc=6,abc/2ab+2ac=8。这时候把它们倒数相加就得到
2(ab+ca+bc)/abc=1/3+1/6+1/8=5/8。长方形体积与表面积的比为8/5。7-2(六年级)如图,四边形ABCD中,AD=CD=BC,∠C=90°,∠D=150°,则∠ABC=?作正方形BCDE,连接AE.△ADE为等边三角形,△AEB为等腰三角形,所以,∠EAB=∠EBA=15°,∠ABC=90-15=75°。8、设a、b、c、d是1-9之间的四个不同数字,用这四个数字(不能重复)可以组成很多不同的四位数,小明把所有可能组成的四位数加起来,但他不小心把其中一个四位数多加了一遍,结果为128313,那么,正确的结果应该是?用a、b、c、d这四个数字可以组成24(4×3×2×1)个不同的四位数,并且a、b、c、d在个位、十位、百位、千位各出现6次.所以这24个不同的四位数的和为:
(a+b+c+d)×6×1111=6666(a+b+c+d),
设被多加的四位数为x,则6666(a+b+c+d)+x=128313
128313/6666=19……1659,考虑到x小于10000,所以,a+b+c+d也可能等于18(千万不要遗漏)
代入检验,当a+b+c+d=19时,余数1659各位相加=21,不符合题意。当a+b+c+d=18时,余数8325各位相加=18。得正确结果是18×6666=119988。
9(五年级)在任意n个正整数里,必有两个数,它们之和或差能被50整除,最小的正整数n为?考察抽屉原理。我们可以按被50除时可得到的50个余数0、1、2、…、48、49,设计26个“抽屉”:{0}、{1,49}、{2,48}、…、{24,26}、{25}。根据抽屉原理,27个数中必有两个数,它们除以50所得的余数落在同一个“抽屉”里。因为如果它们余数相同,其差能被50整除,如果它们余数不同,则它们的和能被50整除。因此n=27。10、棱长为1的正方体的6个面分别标有不同的点数,下图是从不同角度观察同一个正方体的四种情形,若将10个完全相同的正方体粘合成一个1×1×10的长方体,则长方体表面标记的点数和的最大值是?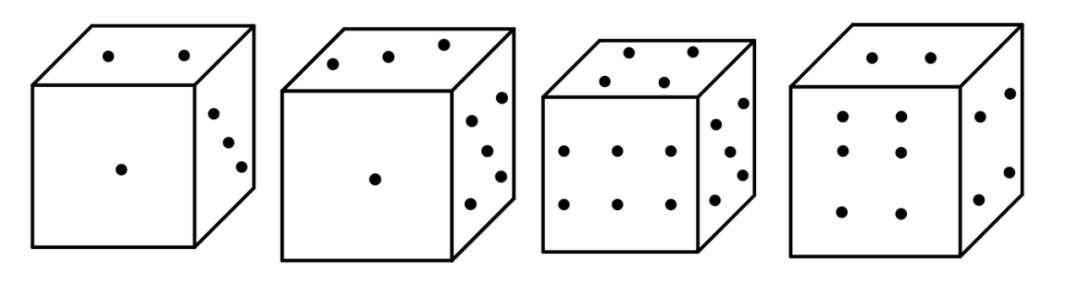
经观察,图中正方体为标准的骰子,相对面的点数和相等为7。10个完全相同的正方体粘合在一起,中间8个正方体露在外面的总是两组相对面,点数和为14,无论怎么摆放不影响结果。对于两边的正方体,粘合后有5面在外,要使点数和最大,将1放在粘合面即可。结果=14×8+20×2=152。二、解答题(满分60分,11-13题各10分,14/15题各15分)
11-1(五年级)计算:1/7×(13.21×77/25-3.75÷19/21)+(15/4÷19/41+13.46×14/25)11-2(六年级)计算:1/4×(4.85÷5/18-3.6+6.15×18/5)+[5.5-1.75×(5/3+19/21)]答案:10。
12、某校学生志愿者社团成员的五分之一安排做交通协管员,有52名成员在医院做义工,还有若干个学雷锋小组派到各社区服务,每个小组都由社团的七分之一成员组成,问该学生志愿者社团共有成员多少人?设该学生社团共有成员n人,有k个学雷锋小组,每个学雷锋小组n/7人,根据题意可列方程:n=n/5+52+kn/7,n=52×35/28-5k。因n、k均为自然数,k只能为3,此时n=140人。
13、如图,直角梯形ABCD,AD∥BC,∠BAD=90°,AD=AB=2BC=2,连接对角线AC、BD交于O,求图中阴影部分面积。
这题官方给画了辅助线,但事实上不太需要。用相似三角形的性质即可处理。
因AD:BC=2:1,可知AO:OC=DO:OB=2:1,设S△OBC=x,S△A0B=2x,S△COD=2x,S△AOD=4x。S梯形ABCD面积=3=9x,解得x=1/3,阴影部分面积=4x=4/3。
14-1(五年级)把1到70的所有自然数平均分为两组,将每组的35个数乘起来求积,然后将所得的两个积相加,所得和数称为一个“鹏程数”。证明下面两小题:
(2)若一个“鹏程数”不是2的倍数,则这个“鹏程数”是2015的倍数。(1)把1到70平分为两组,设其中一组的乘积为a,另一组的乘积为b,因为70中有35个奇数和35个偶数,所以分组后只有两种情况:第一种,第一组中和第二组中均有偶数,那么a和b也都会是偶数,a+b是合数;第二种,第一组全是奇数,第二组全是偶数,这时,把第二组中的偶数都除以2,会出现1、3、5、7、…、35这些因数,a和b有共同的因数1×3×5×7……×35,所以,“鹏程数”必是合数。
(2)若一个“鹏程数”不是2的倍数,即为(1)题中的第二种情况,一个“鹏程数”有因数1×3×5×7……×35,因2015=5×13×31。所以“鹏程数”是2015的倍数。14-2(六年级)具有以下性质的自然数叫“鹏程数”:(1)在它的各个数位上,除数字0外,数字1-9都出现过,(2)任何相邻的两个数位上的数字所组成的两位数都是17或23的倍数,例如:923468517就是一个9位的鹏程数,试证明2015位的“鹏程数”必定是合数。两位数中,17的倍数有17、34、51、68、85;23的倍数有23、46、69、92,可见其中1、2、3、4、5、8、9都出现了2次,7出现了1次,6出现了3次。也就是说,当出现1、2、3、4、5、8、9时,前后数字是可以唯一确定的,而到了7将终止,所以7只能在个位出现。
如果我们从左向右分析,当出现6的时候有2种情况,第一种情况:6后面跟着9,那么接着可以选择2、3、4、6,会出现92346的5位循环,第二种情况,6后面跟着8,那么接着可以选择5、1、7,数字循环终止。
所以,我们考虑这个2015位的鹏程数一定是前面是n个92346循环,再加上8517小尾巴(因为1-9都要出现,所以这个小尾巴不能省)。题目其实给了提示,如果你拿923468517这个数再往前推,也能发现这个规律。
2015/5=403,可得2015位的鹏程数可以表示为6-92346-92346…(共402组)…92346-8517。要判断是不是合数,我们最先可以想到的是计算数字和。此数数字和=6+24×402+21。不用计算即可知是3的倍数。15、证明下面两小题。
(1) 试证明:直线上存在4个点,使得这4个点两两之间的个距离恰为1、2、3、4、5、6这六个值;
(2) 在直线上是否存在5个点,使得这5个点两两之间的个距离恰为1、2、3、4、5、6、7、8、9、10这十个值?如果存在,请举一例:如果不存在,请说明理由。(1)解释起来比较复杂,作图最直观。如下即可以实现。
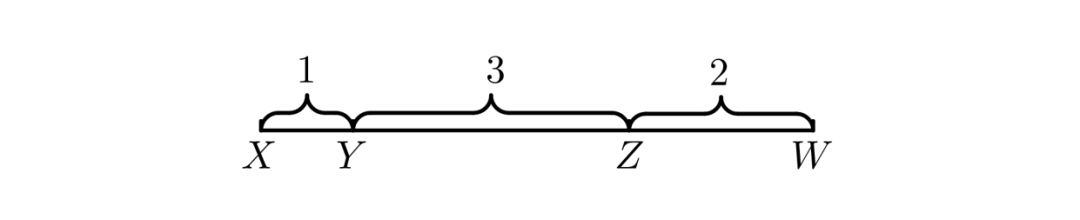
(2)作图如下

方法一:设直线上存在适合于题设条件的个点,它们依次是A、B、C、D、E;记两两之间的个距离之和为S,其中AE=10.依题意有S=1+2+3+4+5+6+7+8+9+10=55。
另一方面:
S=AB+AC+AD+AE+BC+BD+BE+CD+CE+DE=(AB+BE)+(AC+CE)+(AD+DE)+AE+BC+BD+CD=40+2BD。得出结果必为偶数,与S=55矛盾,题目假设不存在。方法二:正常来说,压轴题的(2)问会建立在(1)问基础上,如果用方法一解题,好像与(1)问没有什么联系。所以考虑另外一种解法。我们先从(1)问的线段观察起,发现,我们可以把XY、YZ、ZW看成3段小棒,它们通过连接组成不同的长度,其中两端的小棒可以用3次,中间的小棒可以用4次。我们把需要组成的值分解,得到合计需要3个1、3个2、4个3即可满足题意,其中3放在中间,1、2放在两端。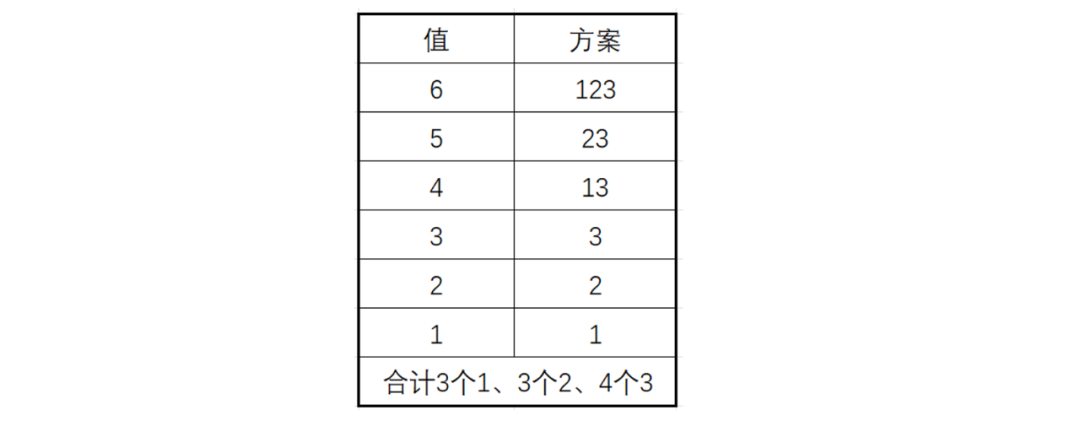
当条件变成5个点4个线段时,通过奇偶性,不需要如上分解即可解题。我们按照上述方法把AB、BC、CD、DE看成是4段小棒,在拼接中,两端的AB、DE用到4次,中间的BC、CD用到6次,即4(AB+DE)+6(BC+CD)需要等于55,同样可以证明无解。
2015年五年级一、二、三等奖比例及分数为3%(84分)、7%(54分)、15%(35分)。
2015年六年级一、二、三等奖比例及分数为3%(87分)、7%(71分)、15%(51分)。















全部 0条评论