
第一部分:试题
1、在下面的加法算式中,不同的汉字代表不同的数字,当算式成立时,和数“开赛大吉”的最小值是?
2(同五年级)x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地多少亩?
3(同五年级)设a=1+2+2²+2³+2^4+…+2^999+2^1000,则a被3除的余数是?
4(同五年级)某班教室全部是双人课桌,被学生坐满没有空位.其中60%男学生的同桌也是男生,而20%女学生的同桌也是女生.那么,这个班的女生占全班学生总数的多少?
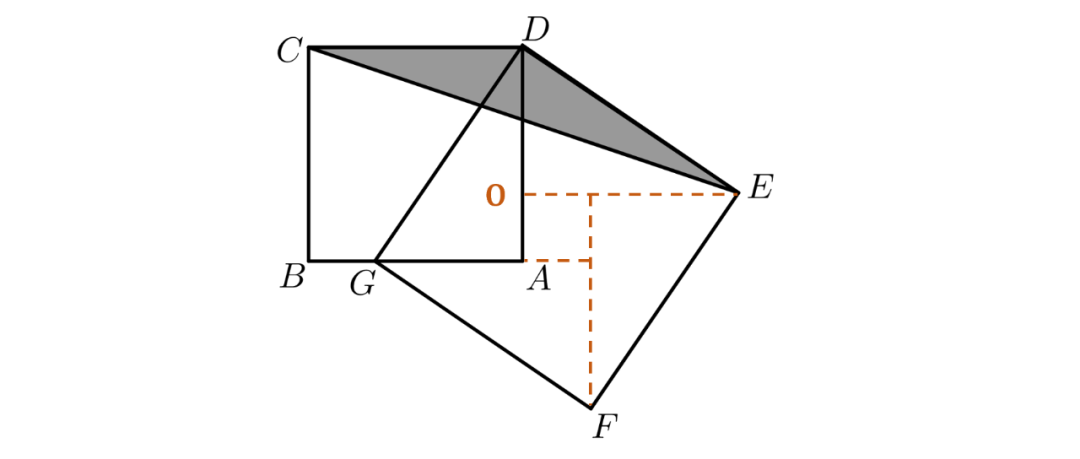
5、如图,ABCD和DEFG都是正方形,面积分别为9平方厘米和13平方厘米,G在线段AB上,则三角形CDE的面积等于多少平方厘米?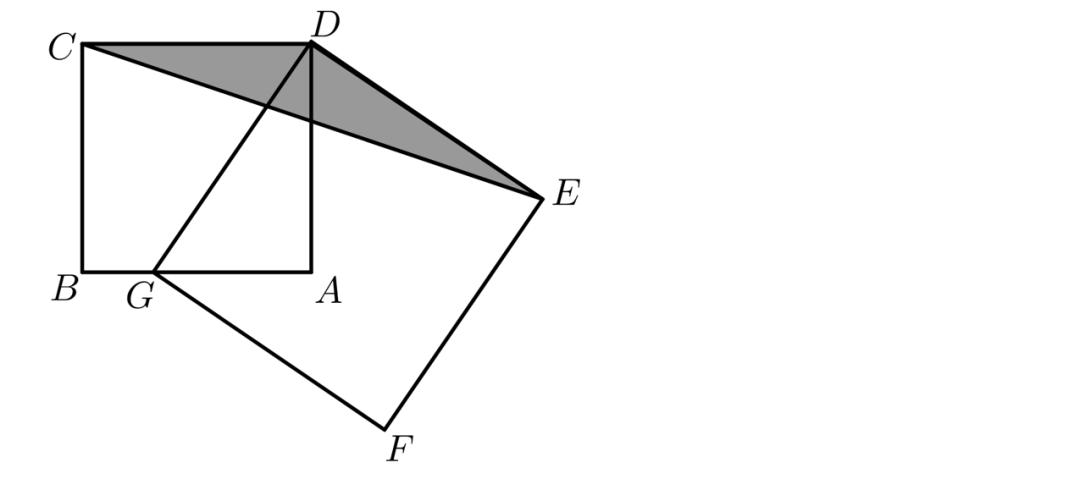 6(同五年级)某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?
6(同五年级)某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?
7、自然数b与175的最大公因数记为d,如果176×(b-11×d+1)=5×d+1,则b=?
8、有两个小正方体,每个正方体的六个面上都分别写有1到6这六个数字。现将两个小正方体投掷到桌面上,要保证有两次两个小正方体朝上面上的数字之和相同,需至少投掷多少次?9、一个正方体的每个顶点都有三条棱,以其为端点沿这三条棱的三个中点,从这个正方体切下一个角.这样一共可切下八个角.则余下部分的体积(图中的阴影部分)和正方体体积的比值等于?10、沿着圆圈列出的十个数码,按顺时针次序可以组成许多个整数部分是一位的循环小数.例如1.892915929(15929循环)等等,那么在所有这种数中最大的一个是?

二、解答题(满分60分,其中第11-13题各10分,第14/15题各15分)11、如图所示AB=BC=CA=AD=30,且∠CDB=2∠ADB。
(1)求证:DA⊥CA。
12、某校运动会在400米环形跑道上进行10000米的比赛,甲、乙两名运动员同时起跑后,乙的速度超过甲的速度,在第15分钟时甲加快速度,在第18分钟甲追上乙并且开始超过乙,在第23分钟时甲再次追上乙,在第23分50秒时甲到达终点。那么乙跑完全程用的时间是多少分钟?
13(同五年级)象棋比赛共有奇数个选手参加,每位选手都同其他选手比赛一盘。胜一盘得1分,平1盘得0.5分,负一盘得0分。已知其中两名选手共得8分,其他人的平均分数为整数。求参加此次比赛的选手共有多少人?
14(同五年级)定义运算∣a-b∣= a-b(a≥b)或b-a(a≤b),在1、2、3、4、5、6、7、8、9、10这10个数中,任意选5个,从小到大依次记为a1、a2、a3、a4、a5,剩下5个数从大到小依次记为b1、b2、b3、b4、b5,证明∣a1-b1∣+∣a2-b2∣+∣a3-b3∣+∣a4-b4∣+∣a5-b5∣=25。
15(同五年级)平面上有7个点,其中任意三个点不共线,以这7个点为顶点作三角形,使得任何两个三角形至多只有一个公共点,由此最多可作多少个满足条件的三角形?并请举出一个例子。
第二部分:解析
1、在下面的加法算式中,不同的汉字代表不同的数字,当算式成立时,和数“开赛大吉”的最小值是?
让四位数尽可能小,最好是实现102X。千位是1、百位是0、十位是2,都需要进位才能实现。也就是说我们从3、4、5、6、7、8、9这几个数里面要构建出一个9、一个11、一个1X。同时,要考虑9这个数只能放在个位(9+3至少等于12),而9加上一个数所得的数的个位是比加数小1的数,所以构建完9和11后,剩下的两个非9 的数需要是连续的。
综上,我们考虑构建4+5=9、3+8=11、9+7=16。即439+587=1026。“开赛大吉”的最小值是1026。
2(同五年级)x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地多少亩?
1台拖拉机1天1小时可耕地x/x·x·x=1/x²,故y台拖拉机,每天工作y小时,y天耕地y³/x²亩。3(同五年级)设a=1+2+2²+2³+2^4+…+2^999+2^1000,则a被3除的余数是?
因为a=1+2(1+2)+2³(1+2)+…+2^999(1+2),a被3除的余数是1。
4(同五年级)某班教室全部是双人课桌,被学生坐满没有空位.其中60%男学生的同桌也是男生,而20%女学生的同桌也是女生.那么,这个班的女生占全班学生总数的多少?
由题意可知,40%的男同学数=80%的女同学数,男女同学数之比为2:1,女生占总数1/3。5、如图,ABCD和DEFG都是正方形,面积分别为9平方厘米和13平方厘米,G在线段AB上,则三角形CDE的面积等于多少平方厘米?
构造弦图,得OE=AD,OD²+OE²=DE²,解得OD=2,OD即为△CDE在CD边上的高,S△CDE=3×2×1/2=3平方厘米。6(同五年级)某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?
设乘客数=12k。正常来说,每10个号码中有1个7在末尾,比例应该是1/10,出现1/12的情况在于增加了其他数稀释。总共可以用来稀释的一共有9个数,所以k最大为4,乘客最大数量为48。如列不等式,12k<10(k+1),也可求得k小于5。同样,也可以测算枚举,发现k=1、2、3、4、5时,7所占的比例下限是1/19、2/29、3/39、4/49、5/59,其中5/59大于1/12。k最大为4。7、自然数b与175的最大公因数记为d.如果176×(b-11×d+1)=5×d+1,则b=?
因d是b与175的最大公因数,所以d必然是175的因数。175分解质因数=5×5×7,d的可能值是1、5、7、25、35、175。考虑176×(b-11×d+1)=5×d+1成立,而等式出现的数都是自然数,即(b-11×d+1)是自然数。可知d有两个限制条件:(1)5d+1≥176,d≥35,d只能为35或175。(2)(5d+1)/176为整数,得d只能为35。
8、有两个小正方体,每个正方体的六个面上都分别写有1到6这六个数字.现将两个小正方体投掷到桌面上,要保证有两次两个小正方体朝上面上的数字之和相同,需至少投掷多少次?两个正方体朝上面上的数字之和最大为12,最小为2,共11种情况,所以投12次就可以保证有两次朝上面上的数字之和相同。
9、一个正方体的每个顶点都有三条棱,以其为端点沿这三条棱的三个中点,从这个正方体切下一个角.这样一共可切下八个角.则余下部分的体积(图中的阴影部分)和正方体体积的比值等于?设正方体的边长为2,体积为8。直三棱锥底面两个直角边长均为1,高也为1,体积=1/3×(1×1×1/2×1)=1/6。8个的体积即为8/6,占正方体体积1/6。所以,余下部分的体积和正方体体积之比是5/6。10、沿着圆圈列出的十个数码,按顺时针次序可以组成许多个整数部分是一位的循环小数.例如1.892915929(15929循环)等等,那么在所有这种数中最大的一个是?
要使循环小数最大,首先应保证循环小数对应的基础小数最大。经观察,从3开始所得的小数9.291892915最大。循环节选择92915所得的循环小数最大,即:9.291892915(92915循环)。二、解答题(满分60分,其中第11-13题各10分,第14/15题各15分)11、如图所示AB=BC=CA=AD=30,且∠CDB=2∠ADB。(1)求证:DA⊥CA。
(2)求△ABD的面积。

延长BA,并作D到BA延长线的垂线,交于O点。
(1)设∠ADB=x,因AB=AD,故∠ABD=∠ADB=x。另∠CDB=2∠ADB=2x,同时,因AC=AD,∠ACD=∠ADC=3x。因△ABC是等边三角形,∠BCD=60°+3x,∠DBC=60°-x,在△BCD内,可知,60°+3x+60°-x+2x=180°,x=15°。∠OAD=30°。∠DAC=90°。命题得证。(2)OD是△ABD在AB边上的高,因∠OAD=30°,可知OD=1/2AD=15,S△ABD=AB×OD×1/2=30×15×1/2=225。12、某校运动会在400米环形跑道上进行10000米的比赛,甲、乙两名运动员同时起跑后,乙的速度超过甲的速度,在第15分钟时甲加快速度,在第18分钟甲追上乙并且开始超过乙,在第23分钟时甲再次追上乙,在第23分50秒时甲到达终点.那么乙跑完全程用的时间是多少分钟?对于复杂应用题,我们先把题目给的信息梳理解析一下:
[甲15分钟时加速,18分钟追上乙]:也就是前面15分钟甲比乙慢的距离甲加速后用3分钟追上了。即前面甲比乙慢的速度与后面甲比乙快的速度比为1:5。
[18分钟追上乙,23分钟再次追上乙]:也就是甲加速后5分钟可以比乙多跑400米,每分钟快80米。
结合以上两点,可知初始加速比乙速慢16米/分钟,加速后比乙速快80米/秒。
设乙速x,可得方程(b-16)×15+(b+80)×53/8(8分50秒)=10000。解得b=400。乙跑完全程25分钟。
13(同五年级)象棋比赛共有奇数个选手参加,每位选手都同其他选手比赛一盘.胜一盘得1分,平1盘得0.5分,负一盘得0分。已知其中两名选手共得8分,其他人的平均分数为整数。求参加此次比赛的选手共有多少人?
设共有n个选手参加比赛,依题意n个选手共赛[n×(n-1)] / 2盘,依据记分规则,每盘双方选手合计可以得1分,即总分为[n×(n-1)] / 2分。已知其中两名选手共得8分,其他人的平均分为整数,得{ [n×(n-1)] / 2-8}/ n-2是整数,整理得(n+1)/ 2-7/(n-2)是整数。解得n=9,参加此次比赛的选手共有9人。14(同五年级)定义运算∣a-b∣= a-b(a≥b)或b-a(a≤b),在1、2、3、4、5、6、7、8、9、10这10个数中,任意选5个,从小到大依次记为a1、a2、a3、a4、a5,剩下5个数从大到小依次记为b1、b2、b3、b4、b5,证明∣a1-b1∣+∣a2-b2∣+∣a3-b3∣+∣a4-b4∣+∣a5-b5∣=25。
拿到题目,先要思考,25是怎么来的,推算可知10+9+8+7+6-5-4-3-2-1=25。到这里我们就可以把题目转化为证明a1b1、a2b2、a3b3、a4b4、a5b5这五对数里面,均是一个>5,一个≤5。用反证法,假设a1、b1均≤5,因b1是b1-b5中最大的,如假设成立,需要b2-b4都≤5,这样合计有6个数≤5,不成立。反之,如果a1、b1均>5,因a1是a1-a5中最小的,如假设成立,需要a2-a4都>5,这样合计有6个数>5,也不成立。因此,a1、b1中一定有一个数>5,一个数≤5。用同样方法可推出后续每组亦如此。原式=10+9+8+7+6-5-4-3-2-1=25,命题得证。
15(同五年级)平面上有个7点,其中任意三个点不共线,以这个点为顶点作三角形,使得任何两个三角形至多只有一个公共点,由此最多可作多少个满足条件的三角形?并请举出一个例子。
平面上7个点,任意三个点不共线,两两连接共有(7×6)/2=21条线段。又由于任何两个三角形至多只有一个公共点,说明任意两个三角形都没有公共边,因此,最多只能有21/3=7个三角形。可以构造一个如图下图形:设个点分别为A1、A2、A3、A4、A5、A6、A7。则图中的△A1A2A3,△A1A4A5、△A1A6A7、△A2A4A6、△A2A5A7、△A3A4A7、△A3A5A7。



 6(同五年级)某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?
6(同五年级)某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?











全部 0条评论