
第一部分:试题
2015×20162016-2016×20152015=?
2、x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地多少亩?
3、设a=1+2+2²+2³+2^4+…+2^999+2^1000,则a被3除的余数是?
4、某班教室全部是双人课桌,被学生坐满没有空位.其中60%男学生的同桌也是男生,而20%女学生的同桌也是女生.那么,这个班的女生占全班学生总数的多少?
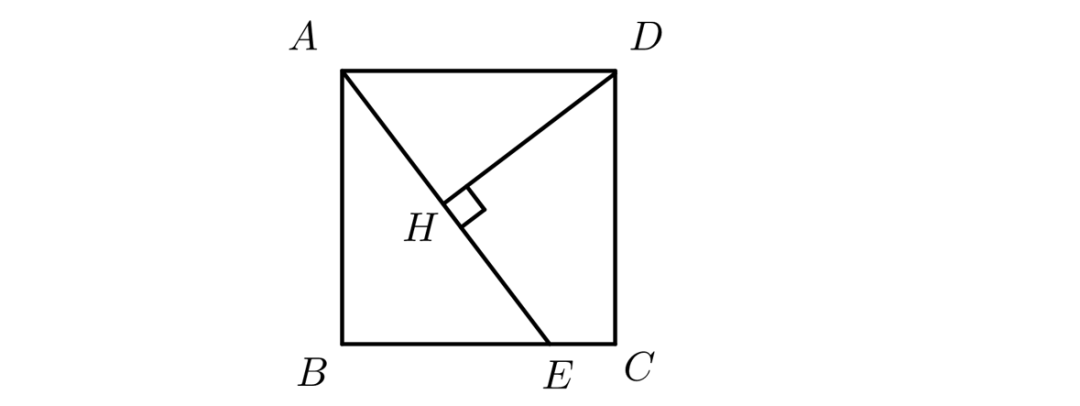
5、如图,ABCD是正方形,边长4,E是BC边上一点,CE=1,D点到AE的距离(从D向AE作垂直,若垂足为H,记为DH)是多少?
6、某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?7、一个自然数a乘7后,乘积的最后三位数是319,那么a的最小值是?
8、今天是2016年3月19日,是第三届“鹏程杯”数学邀请赛的比赛日,请在右图每个□中填入一个数字,使得算式成立,那么乘积是?
9、如图,把A、B、C、D四个区域用四种不同的颜色着色,且相邻的两个区域不能使用同一种颜色,不同的区域可以使用相同的颜色,那么,这幅图一共有多少种着色方法?
10、一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形,其中三个长方形的面积如图所示,第四个长方形的面积是?
二、解答题(满分60分,其中第11-13题各10分,第14/15题各15分)11、如图所示,平行四边形ABCD,AB∥CD,AD∥BD,E是AD上的点,线段CE、BD交于F,已知EF/FC=λ,求四边形ABCE与三角形CDE面积的比值。
12、在一条公路上,甲、乙两个地点相距600米。张明每小时行走4千米,李强每小时行走5千米。8点整,他们两人从甲、乙两地同时出发相向而行,1分钟后他们都调头反向而行,再过3分钟,他们又调头相向而行,依次按照1、3、5、7…(连续奇数)分钟数调头行走。那么,张、李两人相遇时是8点几分?
13、象棋比赛共有奇数个选手参加,每位选手都同其他选手比赛一盘。胜一盘得1分,平1盘得0.5分,负一盘得0分。已知其中两名选手共得8分,其他人的平均分数为整数。求参加此次比赛的选手共有多少人?
14、定义运算∣a-b∣= a-b(a≥b)或b-a(a≤b),在1、2、3、4、5、6、7、8、9、10这10个数中,任意选5个,从小到大依次记为a1、a2、a3、a4、a5,剩下5个数从大到小依次记为b1、b2、b3、b4、b5,证明∣a1-b1∣+∣a2-b2∣+∣a3-b3∣+∣a4-b4∣+∣a5-b5∣=25。
15、平面上有7个点,其中任意三个点不共线,以这7个点为顶点作三角形,使得任何两个三角形至多只有一个公共点,由此最多可作多少个满足条件的三角形?并请举出一个例子。
第二部分:解析
2015×20162016-2016×20152015=?
同2015年第n题,原式=20152016×10001-2016×2015×10001=0。
2、x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地多少亩?
1台拖拉机1天1小时可耕地x/x·x·x=1/x²,故y台拖拉机,每天工作y小时,y天耕地y³/x²亩。3、设a=1+2+2²+2³+2^4+…+2^999+2^1000,则a被3除的余数是?
因为a=1+2(1+2)+2³(1+2)+…+2^999(1+2),a被3除的余数是1。
4、某班教室全部是双人课桌,被学生坐满没有空位.其中60%男学生的同桌也是男生,而20%女学生的同桌也是女生.那么,这个班的女生占全班学生总数的多少?
由题意可知,40%的男同学数=80%的女同学数,男女同学数之比为2:1,女生占总数1/3。5、如图,ABCD是正方形,边长4,E是BC边上一点,CE=1,D点到AE的距离(若从D向AE作垂直,若垂足为H,记为DH)是多少? 
通过观察,发现DH是△ADE在AE边上的高,△ADE的面积=AD×DC×1/2=8,同时,由题意可知BE=3,通过勾股定理得AE=5,DH=16/5。6、某班次的长途汽车上的乘客的车票编号是连续的六位数.如果它们中恰有1/12车票的号码末位是数字7,那么在这个班次的汽车上载有乘客的最大数量是多少人?
设乘客数=12k。正常来说,每10个号码中有1个7在末尾,比例应该是1/10,出现1/12的情况在于增加了其他数稀释。总共可以用来稀释的一共有9个数,所以k最大为4,乘客最大数量为48。如列不等式,12k<10(k+1),也可求得k小于5。同样,也可以测算枚举,发现k=1、2、3、4、5时,7所占的比例下限是1/19、2/29、3/39、4/49、5/59,其中5/59大于1/12。k最大为4。7、一个自然数a乘7后,乘积的最后三位数是319,那么a的最小值是?
319除以7余数为4,千位凑出余数3可以整除。1000=6(mod7),4000=24(mod7)=3(mod7),a最小为4319。8、今天是2016年3月19日,是第三届“鹏程杯”数学邀请赛的比赛日,请在右图每个□中填入一个数字,使得算式成立,那么乘积是?
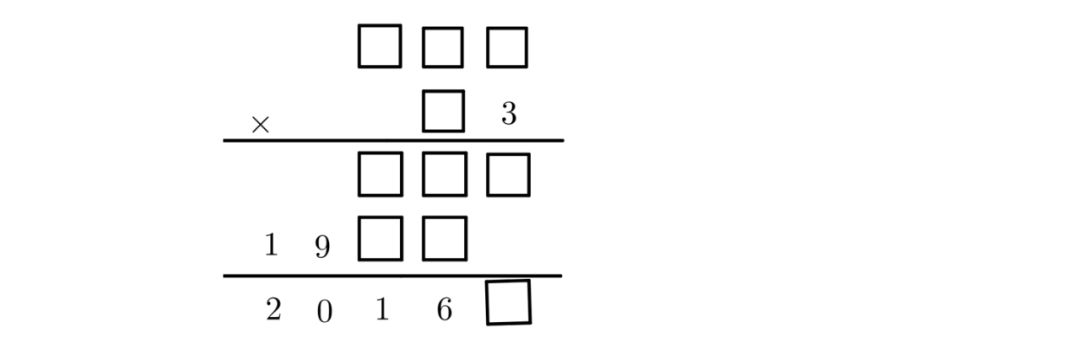
被乘数乘以3不进位,乘以另一个数为19xx,判断,被乘数最高位只能是3或者2。当被乘数的最高位是3时,那么乘数的十位可能是6或5,用20169和6先测算,20169÷63=320……9,得到一解为20160(20160÷63=320);20169÷53=380……29,无解。当被乘数的最高位是2时,那么乘数的十位可能是9或8或7,用20169÷93=216……81(无解);20169÷83=243,得到第二解20169;20169÷73=276……21(无解)。9、如图,把A、B、C、D四个区域用四种不同的颜色着色,且相邻的两个区域不能使用同一种颜色,不同的区域可以使用相同的颜色,那么,这幅图一共有多少种着色方法?
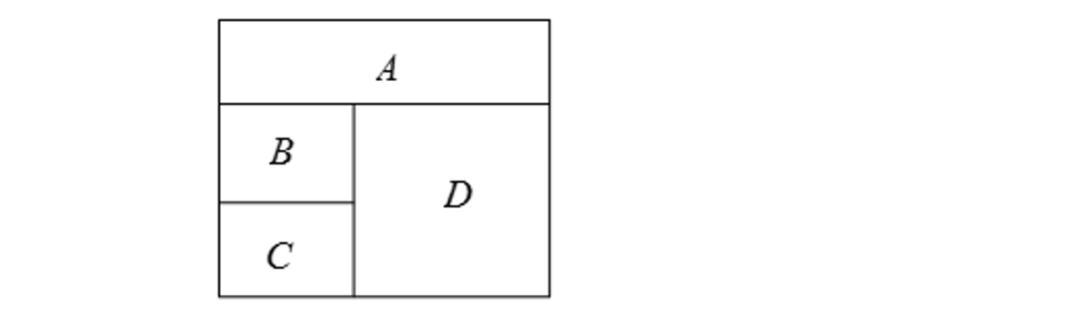
A有4种着色方法,B有3种着色方法,C有3种着色方法,D的着色方法要视C的着色方案考虑。如C选择与AB不同的着色方法(2种),D只有1种着色方法,如果C选择与A相同的着色方法,那么D有2种着色方法。所以,该图共有4×3×2×1+4×3×1×2=48种着色方法。10、一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形,其中三个长方形的面积如图所示,第四个长方形的面积是?
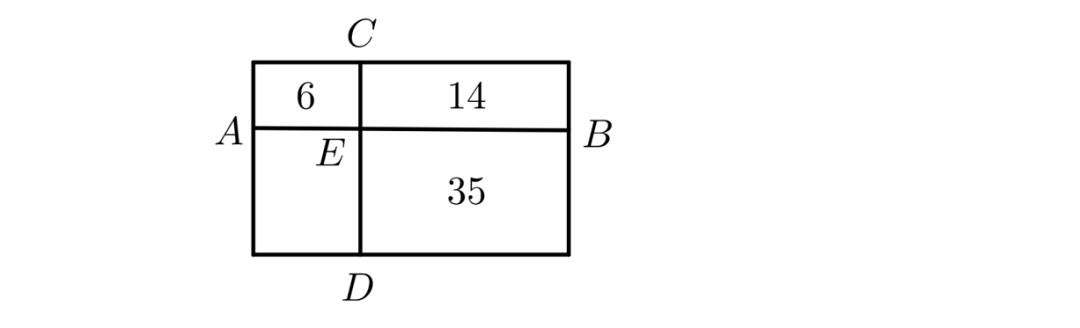
设第四个长方形面积为x,因为下面两个长方形面积比等于上面两个长方形面积比,即x/35=6/14,x=15。二、解答题(满分60分,其中第11-13题各10分,第14/15题各15分)11、如图所示,平行四边形ABCD,AB∥CD,AD∥BD,E是AD上的点,线段CE、BD交于F,已知EF/FC=λ,求四边形ABCE与三角形CDE面积的比值。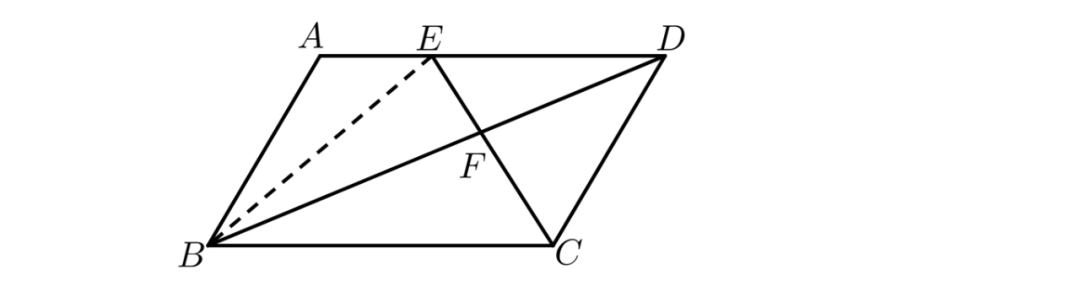
设AD=BC=1,因EF/FC=λ,可知ED/BC=λ,ED=λ,AE=1-λ。四边形ABCE与三角形CDE高相同,面积比=AE+BC/ED=(1-λ+1)/λ=2/λ-1。12、在一条公路上,甲、乙两个地点相距600米.张明每小时行走4千米,李强每小时行走5千米。8点整,他们两人从甲、乙两地同时出发相向而行,1分钟后他们都调头反向而行,再过3分钟,他们又调头相向而行,依次按照1、3、5、7…(连续奇数)分钟数调头行走。那么,张、李两人相遇时是8点几分?
张明、李强每分钟共走(4000+5000)/ 60=150(米),600米需用600 / 150=4(分)。由于两人常常调头,只有当相向而行的时间总和比背向而行的时间总和多4分钟时,两人才能相遇。测算知1+5-3<4,1+5+9-3-7=5>4,所以实际用时间1+3+5+7+9-1=24(分),即两人8点24分相遇。13、象棋比赛共有奇数个选手参加,每位选手都同其他选手比赛一盘.胜一盘得1分,平1盘得0.5分,负一盘得0分。已知其中两名选手共得8分,其他人的平均分数为整数。求参加此次比赛的选手共有多少人?
设共有n个选手参加比赛,依题意n个选手共赛[n×(n-1)] / 2盘,依据记分规则,每盘双方选手合计可以得1分,即总分为[n×(n-1)] / 2分。已知其中两名选手共得8分,其他人的平均分为整数,得{ [n×(n-1)] / 2-8}/ n-2是整数,整理得(n+1)/ 2-7/(n-2)是整数。解得n=9,参加此次比赛的选手共有9人。14、定义运算∣a-b∣= a-b(a≥b)或b-a(a≤b),在1、2、3、4、5、6、7、8、9、10这10个数中,任意选5个,从小到大依次记为a1、a2、a3、a4、a5,剩下5个数从大到小依次记为b1、b2、b3、b4、b5,证明∣a1-b1∣+∣a2-b2∣+∣a3-b3∣+∣a4-b4∣+∣a5-b5∣=25。
拿到题目,先要思考,25是怎么来的,推算可知10+9+8+7+6-5-4-3-2-1=25。到这里我们就可以把题目转化为证明a1b1、a2b2、a3b3、a4b4、a5b5这五对数里面,均是一个>5,一个≤5。用反证法,假设a1、b1均≤5,因b1是b1-b5中最大的,如假设成立,需要b2-b4都≤5,这样合计有6个数≤5,不成立。反之,如果a1、b1均>5,因a1是a1-a5中最小的,如假设成立,需要a2-a4都>5,这样合计有6个数>5,也不成立。因此,a1、b1中一定有一个数>5,一个数≤5。用同样方法可推出后续每组亦如此。原式=10+9+8+7+6-5-4-3-2-1=25,命题得证。
15、平面上有个7点,其中任意三个点不共线,以这个点为顶点作三角形,使得任何两个三角形至多只有一个公共点,由此最多可作多少个满足条件的三角形?并请举出一个例子。
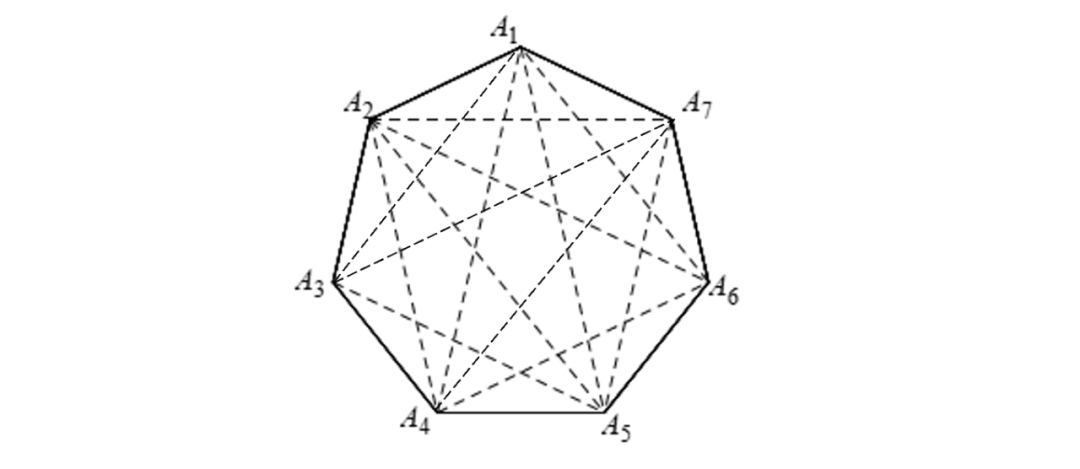
平面上7个点,任意三个点不共线,两两连接共有(7×6)/2=21条线段。又由于任何两个三角形至多只有一个公共点,说明任意两个三角形都没有公共边,因此,最多只能有21/3=7个三角形。可以构造一个如图下图形:设个点分别为A1、A2、A3、A4、A5、A6、A7。则图中的△A1A2A3,△A1A4A5、△A1A6A7、△A2A4A6、△A2A5A7、△A3A4A7、△A3A5A7。

















全部 0条评论