第一部分：试题

1、下面的加法算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。若（程程+杯杯）×鹏鹏－x＝2017，则x＝？

3、若69、90和125被大于1的整数m除的余数都相同。则2017被m除的余数是?

4、某展厅的120盏电灯都是亮着的，每个灯都单独设有开关．现将开关按1-120编号．某同学先按下编号为3的倍数的全部开关，然后再将编号为5的倍数的开关全部按下，那么此时展厅中共有多少盏亮着的灯？

5、一根长为1米的绳子，第1次剪去它的1/2，第2次剪去剩下的绳子的1/3，第3次又剪去剩下的绳子的1/4，……，第2016次又剪去剩下的绳子的1/2017，那么，最后剩下的绳子长为多少米？

6、某停车场有10辆公交车，第一辆公交车出发后，每隔4分钟，有一辆公交车开出。在第一辆公交车开出2分钟后，有一辆公交车进场，以后每隔6分钟有一辆公交车回场，回场的公交车，在原有的10辆公交车以后又依次每隔4分钟开出一辆。问：从每一辆公交车开出后，经过多少分钟，停车场开始出现没有公交车的现象？

7、记号[x]表示不超过x的最大整数，如：[0.9]=0，[2]=2，[3.14]=3等等。则1/[2.1]+1/[6.2]+1/[12.3]+1/[20.4]+1/[30.5]+1/[42.6]+1/[56.7]+1/[72.8]+1/[90.9]=?

8、某人出生于20世纪70年代（出生当年算0岁），他发现从某年起有连续10年，该年年份数字之和都等于自己当年的年龄数，那么这个人2017年是多少岁？

9、将一个棱长是整数厘米的长方体的表面都涂满红色，然后将该长方体分割成若干个棱长为1厘米的小正方体，若其中任何一面都没有涂色的小正方体共有11个，则原来的长方体的体积为多少？

10、给出六位数A和B．数A由偶数码组成，数B由奇数码组成，而数C=A+B的偶数码与奇数码是交替排列的．则C的最大值是？

11、[（1.4+1.6×9/4）×（1÷8/19-2.375）]+2.017

12、甲乙二人分别从A、B两地同时相向出发，往返于A、B之间．第一次相遇在距A地30千米处，第二次相遇在距A地60千米处，求A、B两地的距离。

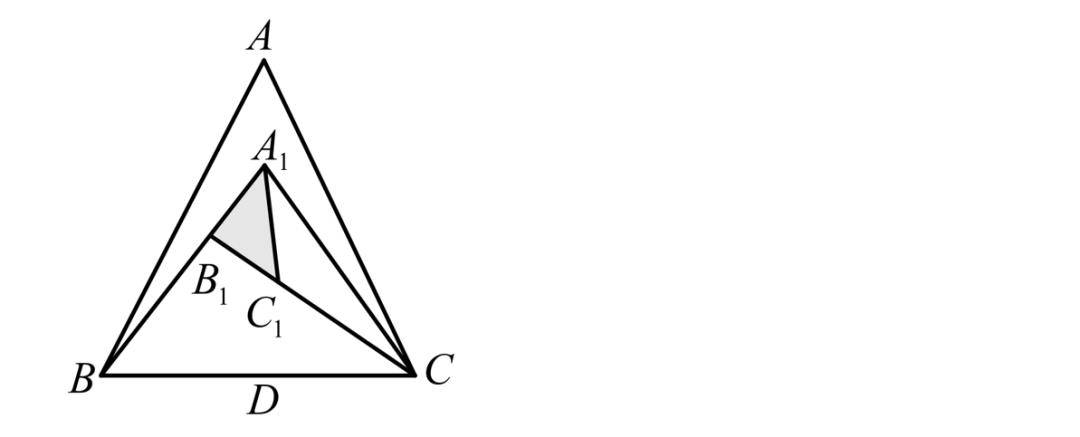
14、1977除本身外有三个约数：1、3、659（注意：659是个质数，也叫素数）。1977的数字和为1+9+7+7=24，它除本身外所有约数的数字和也是1+3+6+5+9=24。我们把具有这种特点的数叫鹏程数，以下是8000以内的鹏程数：

6,33,87，？，303,519,573,681,843,951,1059,   1329,1383,1923,1977,2463,2733,2787,2949,3057,3273,3327,3543,3651,3867,3921,4083,4353,4677,5163,5433,5703,5919,6081,6243,6297,6621,6891,7053,7323,7377,7647,7971。

(1) 用一句话概括什么是鹏程数。

(2) 写出上述数表中遗漏的鹏程数。

(3) 仔细研究上述的鹏程数，找出它们所具备的共同性质，据此提出至少三个猜想。

第二部分：解析

1、下面的加法算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。若（程程+杯杯）×鹏鹏－x＝2017，则x＝？

从个位观察：鹏+程+杯=杯，可推：鹏+程=10，且鹏+程+杯＜20，可以推出在百位的鹏=1，于是：程=9。

从十位观察：鹏+程+杯+1=程，可推：鹏+杯+1=10，因鹏=1，杯=8。

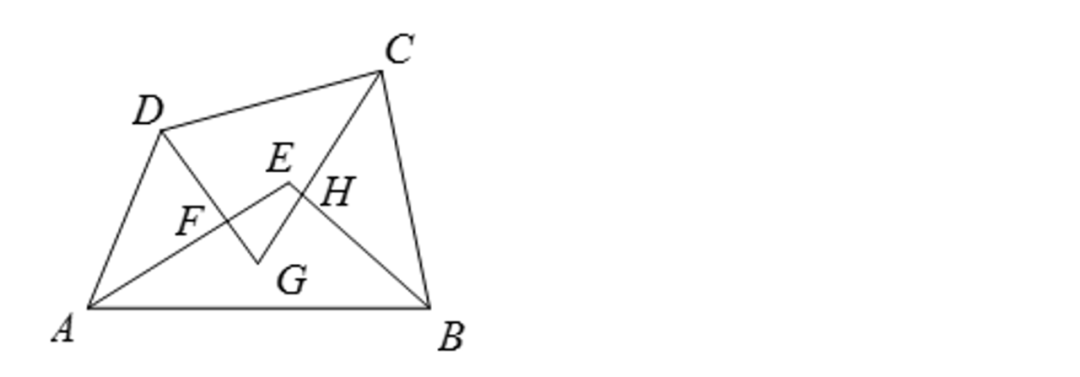
因四边形ABCD的内角和为360°，根据题意，∠EAB+∠EBA+∠GCD+∠GDC是四边形内角和一半=180°。在△GDC和△AEB中，内角和为180°，所以∠EAB+∠EBA+∠GCD+∠GDC+∠AEB+∠CGD=360°，即∠AEB+∠CGD=180°。可知∠CGD=70°。

90-69=21,125-90=35,125-69=56,21、35、56大于1的公因数只有7，因此m=7。2017除以m的余数是1。

编号为3的倍数的灯共40盏，编号为5的倍数的灯共有24盏，编号既是5的倍数又是3的倍数的灯共8盏，这8盏灯因为按了两次重新变亮，因此此时展厅中共有120-（40-8）-（24-8）=120-32-16=72盏灯亮着。

第1次剩下1/2米，第二次剩下1/2×2/3，依次类推，第2016次后绳子剩余1/2×2/3×3/4×…×2016/2017=1/2017米。

设从第一辆公交车驶出直至中断前最后一辆公交车回场的这段时间为x分钟，则驶出的公交车的辆数为x/4+1，而回场的公交车数量为(x-2)/6+1。

由题意，得：x/4+1=（x-2）/6+1+9，解得x=104。

这是表示第一辆公交车驶出104分钟时，停车场只剩下刚刚回场的一辆公交车。显然，再经过4分钟，这一辆公交车驶出后，停车场就没有公交车了。答案为108分钟。

出现连续10年的数字和恰是10个连续的整数，只有可能是1970-1979,1980-1989，1990-1999,2000-2009这4个时间段。

观察发现，1970数字和17，1970-1979明显不符合；1980数字和18，但即使1970年出生，到1980年也才10岁，1980-1989也不符合。1990数字和19，倒推1971年出生符合题意。2000数字和2，2000-2009不符合题意。

9、将一个棱长是整数厘米的长方体的表面都涂满红色，然后将该长方体分割成若干个棱长为1厘米的小正方体，若其中任何一面都没有涂色的小正方体共有11个，则原来的长方体的体积为多少？

因为11是质数，所以，这11个没涂色的小正方体的排列必为“一字形”，故该长方体的长、宽、高必分别为11+2=13、1+2=3、1+2=3，体积为13×3×3=117立方厘米。

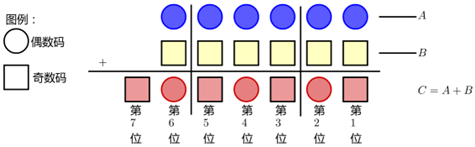
因为数A和B第1位数码是不同的奇偶性，那么数C的第1位数码是奇数．在此时，若没进位，C的第2位将仍是奇数，不符合题意。所以A、B第一位相加产生进位。类似，第3、5、6位都产生进位。在需要进位的位置我们可以选择8+9，使得结果最大。这样即确定了第1、3、5、6位。

第2位和第4位不进位，所以两数相加要小于8，只能为7，所以可以选4+3。

最终得到884848+993939=1878787。

答案=2.017。

本题需分两种情况讨论：

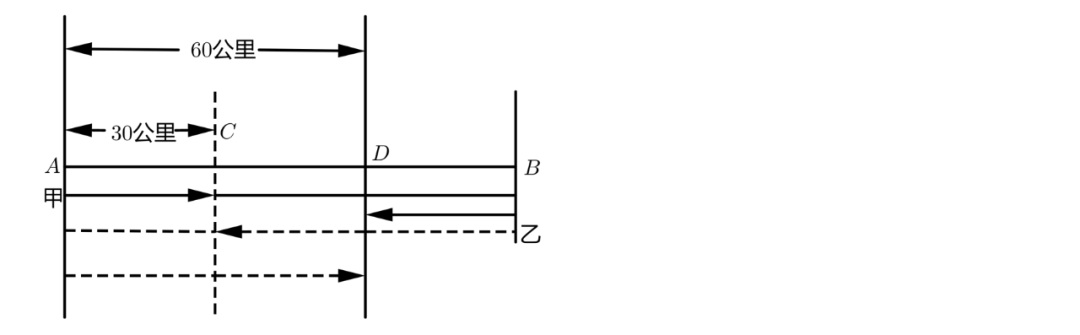
设第一次相遇在C处，甲走30公里，乙走x公里，A、B两地相距（30+x）公里。

（2）第二种情况：第一次相遇后，乙到A地，又返回追上甲，此时甲还未到B地。

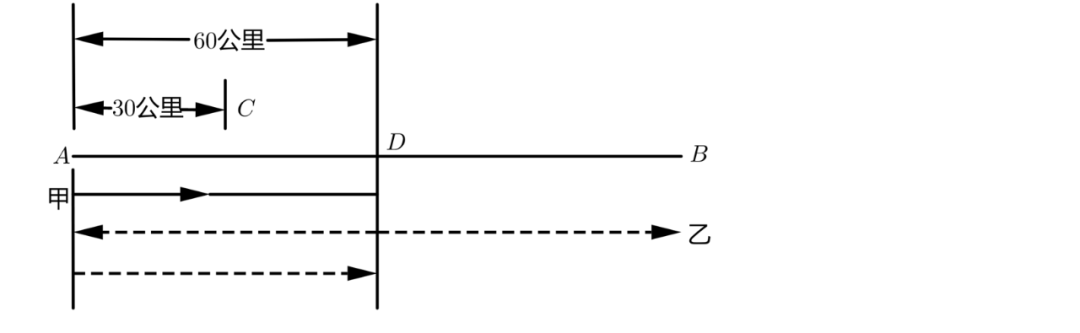
综上，A、B两地距离为75或120公里。

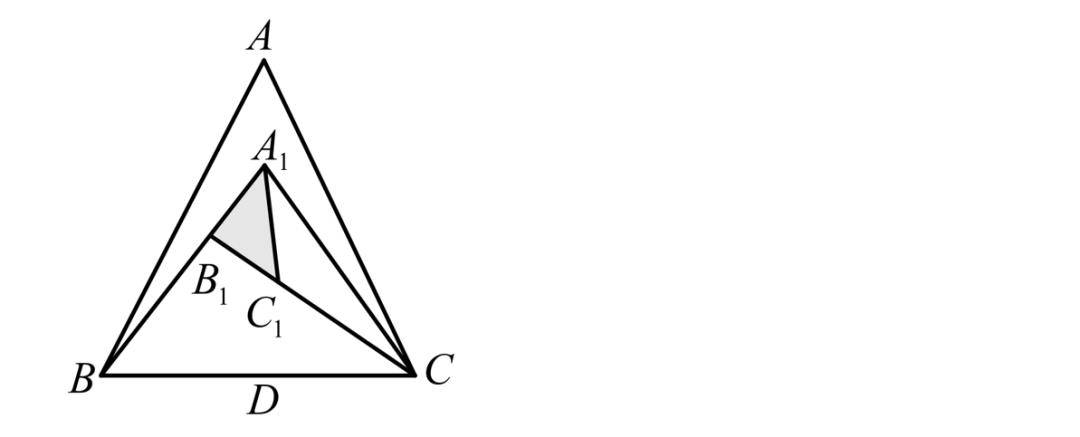
设△A1B1C1面积为x，因B1C1=C1C，所以S△A1B1C=2x。因A1B1=1/3A1B，所以S△A1BC=6x；因AA1=1/3AD，S△ABC=3/2S△A1BC=9x。解得x=1/9，即S△A1B1C1=1/9。

6,33,87，？，303,519,573,681,843,951,1059, 1329,1383,1923,1977,2463,2733,2787,2949,3057,3273,3327,3543,3651,3867,3921,4083,4353,4677,5163,5433,5703,5919,6081,6243,6297,6621,6891,7053,7323,7377,7647,7971。

(1) 用一句话概括什么是鹏程数。

(2) 写出上述数表中遗漏的鹏程数。

（1）一个数的数字和，恰好等于它除本身外的所有约数的数字和，这样的数叫做鹏程数。

15、在一个圆周上有6个点，用线段将它们彼此相连，那么这些线段在圆内最多有多少个交点？请说明理由。

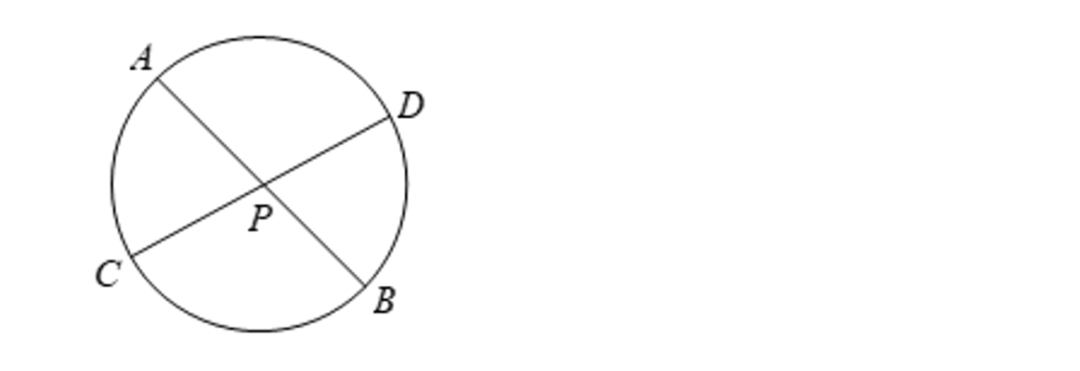
最多有15个交点。

2017年小高组一、二、三等奖比例及分数为3%（83分）、7%（64分）、15%（40分）。