【真题】深圳鹏程杯2014年六年级题(第一届)
一、填空题(满分60分,每小题6分)
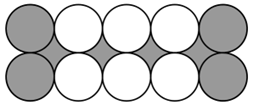
3、如图,10个圆的半径相等,已知阴影部分的面积是48平方厘米,这10个圆的面积之和是多少平方厘米?(π取3.14)
4、桌子上的盘子里放着60块饼干,5个孩子用它来招待客人,每个孩子从盘子里给每个自己认识的客人拿了1块饼干,然后,客人也从盘子里给每个不认识的孩子拿了1块饼干,此时,盘子里的饼干刚好被拿空,在场一共有多少个客人?
5、将一个大正方体积木的六个面都染成红色,然后将这个大正方体切割成n^3个小正方体积木,已知至少有2个面为红色的小积木共有44块,则6个面都没染红的小正方体积木共有多少块?
6、电子钟指示时刻由00:00:00到23:59:59,每个时刻显示1秒钟,如图显示的时刻有两个数字0,那么,在一昼夜期间钟表上显示3个数字7的时刻共有多少秒?

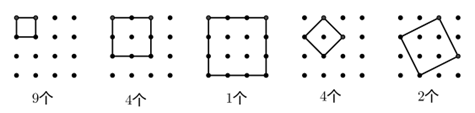
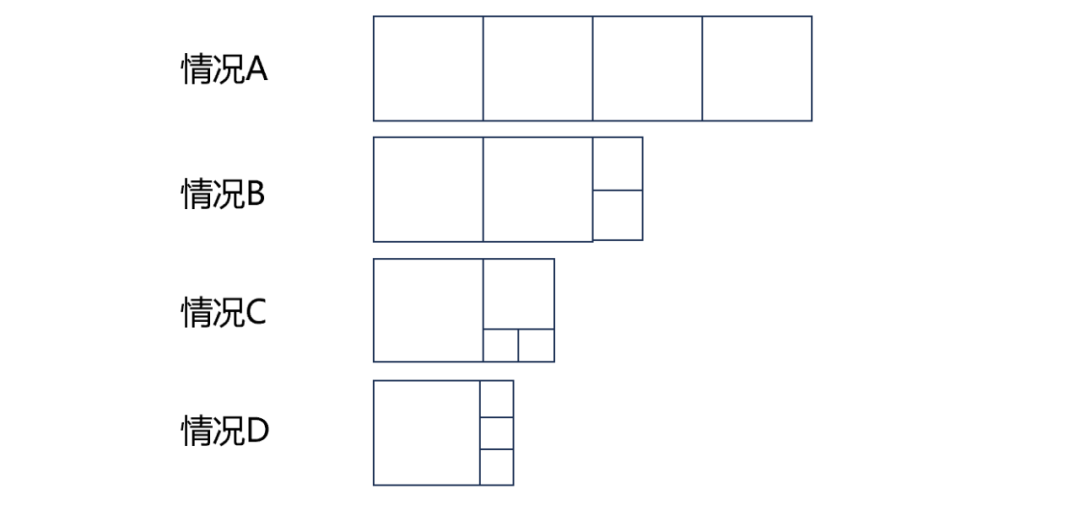
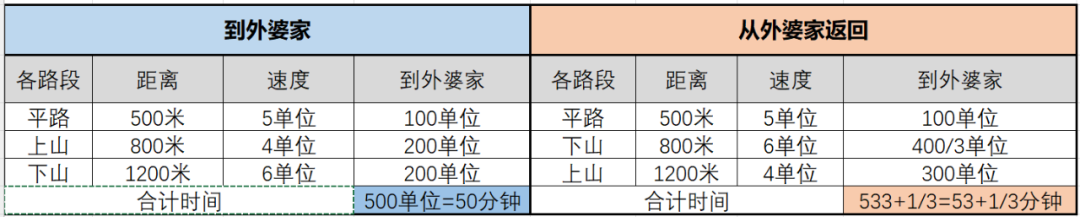
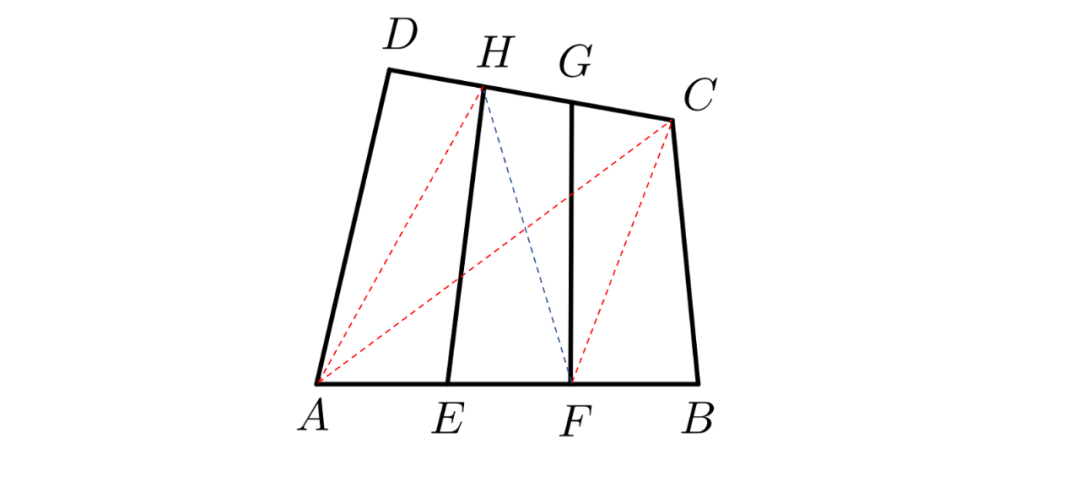
8、已知a与b是互质的自然数,且小于50,则满足1/7 9、一个6位的自然数ABCBCA是7的倍数,则2B+C的最大值等于? 10、已知3个不同的正整数a、b、c它们两两互质,且其中任二数之和都能被第三个数整除,则(a³+b³+c³)/(a²+b²+c²)=? 12、小明家离外婆家有2500米的路程,其中平路占1/5,到外婆家上山路是下山路的2/3,小明从家出发,用50分钟到达外婆家,已知小明上山路的速度比平路慢20%,下山路的速度比平路快20%,照这样计算,小明从外婆家返回家里要走多少分钟? 14、为了准备参加“鹏程杯”数学邀请赛,小明用5天时间共做了31道练习题,每天做题的数量都比前一天有所增加,如果他第一天做题量是第五天的三分之一,那么他第四天做了几道题?简述你的理由。 1、计算: 答案:1584。 数字谜题,寻找解题突破口。观察,等式结果的最高位为2,百位是0,可知,A=1,即BBB+CC-D=2014-1111=903,同理,结果最高位为9,十位为0,可知,B=8,即CC-D=903-888=15,因十位为1,个位要向前进位,得C=2,D=7。 每个孩子认识的客人数加不认识的客人数的和相等,60÷5=12(个)。 通过题中信息“至少有2个面为红色的小积木共有44块”可求出,2个面为红色的小积木共有44-8=36(块),可求出每条棱上上共有积木36÷12+2=5(块),即n=5,则6个面都没染红的小正方体积木共有(5-2)³=27(块)。 9+4+1+4+2=20(个)。 另:对于正方形点阵,有公式如下: 比较与估算题。根据题意可知6a a=1时,b无解; a=2时,b=13; a=3时,b=19、20; a=4时,b=25、27; a=5时,b=31、32、33、34; a=6时,b=37、41; a=7时,b=43、44、45、46、47、48; a=8时,b=49。 所以a/b共有18个结果:2/13、3/19、3/20、4/25,4/27、5/31、5/32、5/33、5/34、6/37,6/41、7/43、7/44、7/45、7/46、7/47、7/48、8/49。 解法一: ABCBCA=100000A+10000B+1000C+100B+10C+A=100001A+10100B+1010C=(14285×7+6)A+(1442×7+6)B+(144×7+2)C。ABCBCA是7的倍数,可知6A+6B+2C是7的倍数。要使2B+C值最大,假设B=9,C=9,此时6B+2C=72,除以7余2,6A如果可取除以7余5的值,则假设成立,经测算,A取2时满足条件。得:2B+C的最大值等于27。 解法二: 因1001是7的倍数,考察一个数是不是7的倍数,可以三位一截,从右向左,用偶数项减奇数项,所得结果除以7与原数同余。 3个数两两互质,且其中任二数之和都能被第三数整除,结果只有1、2、3。 证明:设a>b>c,则2a>b+c,即(b+c)/a<2,由已知(b+c)/a是正整数,故只能(b+c)/a=1,于是a=b+c。因a+c可被b整除,b+2c可被b整除,2c可被b整除。因b、c互质,要使2c被b整除,b只能等于2或1,因b>c,且c是正整数,所以b取2,c取1,a取3。 设长方形纸片宽为a,共分4种情况讨论: 情况A,a=1/4×200=50厘米 情况B,a=2/5×200=80厘米 情况C,a=3/5×200=120厘米 情况D,a=3/4×200=150厘米 通过题意,可知到外婆家的路程中:平路有2500×1/5=500米,上山路有(2500-500)÷(2+3)×2=800米,下山路有2500-500-800=1200米。列张表格清楚得到结果为53+1/3分钟。 第一步,连接AH、AC、CF。因E、F将AB三等分,G、H将CD三等分,所以S△AHC=2/3S△ADC,S△AFC=2/3S△ABC,所以S(四边形AFCH)=S△AHC+S△AFC=2/3(S△ADC+S△ABC)=2/3S(四边形ABCD)=20cm²。 第二步,连接HF。因S△EHF=1/2S△AFH,S△FHG=1/2 S△CFH,S(四边形EFGH)=S△EHF+S△FHG=1/2(S△AFH+S△CFH)=1/2 S(四边形AFCH)=1/2×20cm²=10cm²。 设第一天做题数为a,第五天做题数为3a,因为每天做题的数量都要比前一天有所增加,所以第二、三、四天至少为a+1、a+2、a+3,即7a+6≤31,a≤25/7,a=1或2或3。验证1或2均不能符合题意,所以a=3。即第一天做3题,第五天做9题。第二、三、四天共做题19题。在4、5、6、7、8中选3个数凑成19,只能是4、7、8或5、6、8,第四天做题数只能为8。 15、如果存在连续的n个非零自然数,每个数的质因数分解式(相同的质因数都写成乘方的形式)中,所有质数的指数都是奇数,这样的n个连续自然数称作一组“n的梅花数”, 例如:13=13¹、14=2¹×7¹、15=3¹×5¹就是一组“3朵梅花数”. (2) 试确定n的最大值,并说明理由。 因4个连续自然数中,必有2个偶数,而2个连续偶数,必有一个是4的倍数,即必有一个质因数2的指数是3或更高次,可找到2³×(1或某质数)¹,然后前后寻找符合条件的数,即可找到“4朵梅花数”。 (2) 每8个连续自然数中,必有一个是8的倍数,假设此数为X,X+4或X-4必然在这个连续自然数列中,而此数可被4整除,不能被8整除,分解质因数会出现2²。所以,梅花数中n最大为7。如:29、30、31、32、33、34、35。







全部 0条评论