转出转入都是1:3，只需考虑“净转出”，1016-(1028-1016)/(3-1)=1010人.

每个转盘都是均分，概率相同。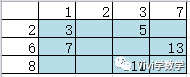。质数概率5/12，故答案为17.

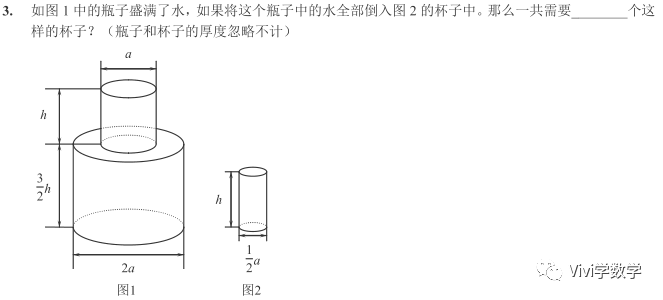
小圆柱：2*2=4杯，大圆柱：4*4*3/2=24杯。4+24=28。

中心不规则图形。舍近求远把外围三角形四边形面积计算了，答案也就有了。

AED面积是ACD面积的1/3故为8；DFC面积为ABCD面积的(1/4)*(1/2)=1/8故为6；EFC面积为ABC面积的(2/3)*(1/4)=1/6故为4，AEFB面积为20。48-8-6-20=14平方厘米.

第一天总数为15的倍数，第二天总数为32的倍数，两天相差41件，故第二天总数个位数必为6，因此可能是32*3、32*8、32*13、32*18、32*23、...且加上14后是17的倍数，最后算得32*58满足，(32*58+14)*8/17=880

但是！线束了吗？从周期来说，必定有更大的数满足题目要求，比如32*（58+5*17*3)+14=10030（既要保持与17的倍余关系，又要保持与15的倍余关系），10030*8/17=4720。以此类推，还有更大的数满足条件。因此，正确答案应该是：880+3840n（n为自然数）。

如果是这样，题目是不是过难了一点（数值也过大）；如果不是这样，题目 是不是出得不严谨。虽然数值越小越“看似更合理”，但从数学的意义上讲，要么多解，要么增加一个条件把多解的可能性封闭掉（比如问最小是多少）。

2x-3y=4斜率2/3小于1，左端点(-1,-2)在y=x下面，则右端点肯定在y=x下面。k=x-y即是直线2x-3y=4到y=x的竖直距离，左端点距离最小为1，右端点(5,2)距离最大为3，1+3=4。

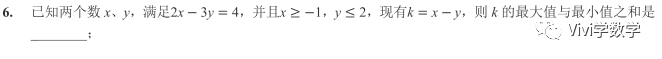
从平均数知最大数在40左右，且数字个数是9的倍数，应为36，总和为716。加上三个擦去的数共39个数，总和(1+39)*39/2=780，三个擦去的数的和为64，两个质数最大可能为37+23或31+29，故为60

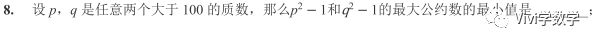
p^2-1=(p+1)(p-1)，p为大于100的质数则必为奇数，p+1与p-1为连续的偶数，则其一个必为4的倍数，即(p+1)(p-1)必为8的倍数。同理(q+1)(q-1)必为8的倍数。那么8就是题目所求吗？找不到实例，心里没底。继续。

将整数看成以6为周期的序列，则p必为6x+1或6x+5（其它必能被２或３整除），所以p+1、p-1其一必为6的倍数，即(p+1)(p-1)必为6的倍数、同时必为8的倍数，所以必为24的倍数。同理q^-1必为24的倍数。所以最小值一定是>=24的数。

两者最大公约数的最小值还有没有可能比24更大？找到实例封印这种可能。如p=103,q=107,102*104=2*3*17*2*2*2*13,106*108=2*53*2*2*3*3*3,最大公约数为2*2*2*3=24。所以最小值为24。完毕。

只看“一倍距离”：轿车追客车用(15+5)/2=10分钟，每分钟比客车快“一倍距离”的1/10；追货车用15分钟，每分钟比货车快“一倍距离”的1/15。所以货车每分钟比客车快“一倍距离”的1/15-1/10=1/30,需30分钟追上客车。30-15-5=10

A、B、C茶树的面积分别用A、B、C表示，总工日A/0.4+B/0.5+C/0.6是20的整数倍，故A/8+B/10+C/12是整数，A=2B代入通分：(42B+10C)/120为整数,则B必为5的倍数。又因A<=270且C<=1.4A，即A>=720/(1+0.5+1.4)=248.28，所以125<=B<=135，排除125和135，故A面积260.

两个最大的群（25个偶数、8个是3的倍数的奇数），所以必须要取34个数才能保证。

每次操作加7，故为1+3+6+8+7*100=728

从钢笔数2360，甲类必为4的倍数，乙类必为5的倍数，则甲乙类笔记本数量都是40的倍数，则丙类必为20的倍数（丙类笔记本总数才可能是40的倍数）。假设丙类20套，变成甲乙类鸡兔同笼问题，(1040-6*20)/40=23，(23*100-(2360-20*20))/(100-80)=17，乙类17*5=85，甲类6*4=24套。24*4+85*7+20*3=751。

继续枚举看有没有多解。假设丙类40套，(1040-6*40)/40=20，(20*100-(2360-20*40))/(100-80)=22，乙类22*5=110>106排除；假设丙类60套，(1040-6*60)/40=17，(17*100-(2360-20*60))/(100-80)=27，则乙类27*5=135>106排除。丙越多则乙必须越多，枚举中止。此题唯一解751.