高思导引系列是学习小奥绕不开的一个门槛，一般有勇气和实力开始刷导引的孩子基础都不会差，并希望通过刷导引过程中提高。经常看到有家长在群里问，高思导引怎么刷，要刷几遍？这个问题我在群里从来不回应，毕竟每个人刷的方式都不一样，如果详细展开那么就是今天这篇文章的篇幅。

如何自鸡高思导引：

《五年级高思导引学习心得》

《四年级高思导引学习心得》

《三年级高思导引学习心得》

介绍高思导引、分析其优点和缺点：

《小奥书籍系列（2.高思导引）》

使用高思导引的建议：

《小学数学鸡娃路线(9.关于高思导引)》

使用高思导引中可能碰到的问题：

《小学数学鸡娃路线(11.关于天天练、高思课本和高思导引的一些问题)》

高思导引答案中可能存在的问题：

《尽信书不如无书-导引答案之浅见》

这一篇展开的角度不一样。不是针对哪一本书，也不是哪一个具体知识点，而是从整体的角度分析这套书的特点，如何最大发挥其作用。

现状

首先，强烈不建议刷导引之前孩子是零基础！

如果还是用第一遍学习知识点的模式来复习，容易出现题目反复错的情况，表现就是：孩子独立做不出来，一提示就会了，然后下次依然做不出来，周而往复。感觉卡在了一个瓶颈，无法继续深入下去，我目前看到的情况，有很多娃止步于此。

【睿爸说明：

刷导引之前的打基础，往往是如下几种情况：

1. 在机构学过相同知识点。

2. 使用录播课自学自鸡过相同知识点。

3. 使用天天练或（和）高思课本等类似小奥教辅学过相同知识点。

一般来说，如果孩子没有额外的辅助，只使用方式3往往是基础最差的情况。】

在有了基础之后刷导引的方式可能有：

第一种方式：报个导引刷题班学习。

机构一般是如下操作，先花10分钟讲一下这节的基础知识，然后就按照顺序把这一讲题目一道道讲下去。先不说这些老师本身的水平如何，仅针对这种授课模式来说，是一种比较初级的学习方式。

假设这个课程2个小时，除去10分钟基础知识，还剩110分钟。一讲导引有10+14+8共32题，为了能讲完只能跳过相当一部分题目。即使这样课堂的进度也飞快，实际上很难把题讲透，其实这个时间能把超越篇的8道题目都讲清楚已经不错了。所以这种蜻蜓点水的刷题班，看起来价格便宜量又足，很适合那些觉得“学过+做过=掌握”的家长。

第二种方式：通过找某些老师录制的导引讲解视频学习。

无论收费还是免费，这些视频我几乎全看过，讲的好的老师凤毛麟角。如果你在看视频时候，发现这个老师讲视频几乎就是把答案读一遍，没有任何思考和试错的过程，那么请马上关闭这个视频，打开导引的答案即可。

看这种视频一个最大的问题就是：所有的步骤都是对的，没有一步遇到过问题，这和实际做题情况严重不符。我们在做题的时候，找到正确方法可能花费整个时间的80%以上，将过程梳理清楚也就是20%，而老师却用了视频100%的时间，讲解了有用的内容20%。这位老师讲解如此流畅丝滑的原因只有一个，他提前看了答案而已。研究答案也是学习的一部分，至少也有思考，但看这种读答案水平的视频就连思考的过程都没有了。

第三种方式：孩子自己刷导引。

孩子刷导引一般都会先做一遍，对完答案后把错题标出来，然后隔段时间再做一遍，也许有第三遍。这种方式的问题我在《尽信书不如无书-导引答案之浅见》里面提到过，导引自己“有问题”的答案不少，这个“有问题”不是说答案是错的，而是不利于更深入地学习。

【睿爸说明：目前看过相对较好的导引刷题课程就是高思自己的91好课，相对较好的导引讲解视频是北京名师C老师早期的课程。】

理念

整套导引虽然分三、四、五、六年级，但是编写时候其实是一个整体，尤其是四、五、六这3本。四、五年级的导引是将小学奥数的关键知识点进行平行展开，而六年级是一个提升。整个系列有2个明显的坡度，做3导的时候，简单题目比较多，感觉导引也就不过如此。到了4导开始不太适应，如果坚持把4导做完，那么5导大概率也能接着做，然后到了6导后，又有一个明显的提升，这也是很多孩子6导做不动或者没做完的原因。

以上的说法就是为了表达，四、五导大概是一个难度水平，完全可以打破限制串联起来。我们都说奥数要提前学，那么导引和大白也可以提前刷，不是说非要跟着书本的目录刷，因为这种安排未必是最合理的。原因如下：

第一个理念就是：把整套书看成一个整体，既要往前看，又要往后看。

具体来说就是每当你做了新的一讲，要重新审视一下以前做的题目。新的知识点和方法，对于解决之前的题目是否有用。

然后再看一下更高年级的导引，有没有难度更大，过程更复杂的题目，看一下除了解决现在这个简单的题目外，如果将题目设置在一个更加复杂的情况下，还需要再考虑哪些因素，能否用现在的知识点解决高阶问题，通过高阶题目来检验是否真的学明白。所以导引刷几遍不重要，怎么刷比较重要，如何刷明白更重要。

既然导引是一个整体，那家长最好就提前全部刷一遍，有时间最好大白也都做完。如果还有时间可以把明心资优的例题都看一遍（不用做题）。这三套书全做透，基本上小奥就不会遇到太大问题，在这个过程中，就看家长和孩子谁先放弃了。

第二个理念就是：按照主线刷题，将相似的题目放在一起，有梯度地做题。

我们都知道小奥一般分为七大模块，导引通过题目的设置把知识点串起来，所以在复习和讲导引的时候，一定要把这些内容也串联起来，否则就失去了它本身最大的价值。

这个主线不是导引的讲次，而是将类似的题目放在一起，而“类似的题目”也有很多种分类方式，可以是相似的具体方法，也可以是相似的解题思想，比如说数形结合的思想，极限的思想，整体考虑的思想，化归的思想等。同一道题目出现在不同的主线里面也很正常，完全决定于你想通过这道题来说明什么。

第三个理念就是：以导引为主线，以大白本和其他练习册为辅助进行巩固。

导引的题目本来数量就少，而且难题最有价值的就是第一遍做的时候，属于不可再生资源，而家长搜集题目比改编题目要容易的多。因此为了解决题量不够的问题，需要补充其他练习册类似的题目。

题目既要源于导引，又能不限于导引，还要超越导引。大白本和明心是不错的选择，当然知名机构的讲义也可以。为什么以导引而不是大白本为主线呢，因为大白本是纯粹的题目集合，并没有清晰的主线。

第四个理念就是：解题方法不应该是老师教的方法，而是通过老师教的方法里提炼出来的自己的方法。我们解一道题不是为了做出答案，而是通过解题掌握这个方法、以及为什么用这个方法。

不过，这个过程对于孩子来说是很困难的，需要高水平的家长和高水平老师的辅导。先不要说家长，就连有这种水平的老师也不是很多。家长有时间可以拿起来书来翻一翻，也许哪天看到了一道题目以后就会有灵感。虽然过程比较花时间，不过和效果相比，这个投入还是值得的。

第五个理念就是：一题多解和多解归一。

这一点无论是理念还是案例已经说过很多，不在赘述。

案例

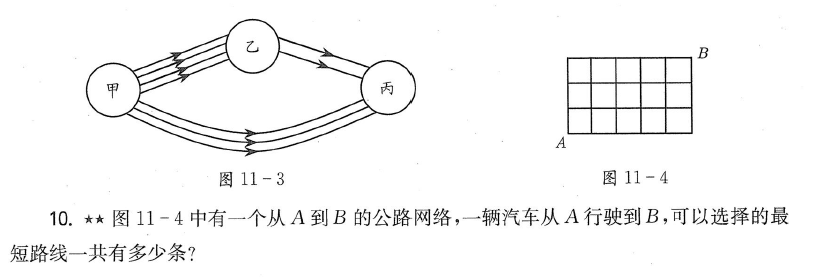
前面说了很多理念，接下来是实际操作阶段。我们先用一道2星题的标数法讲起，下图是4年级导引第11讲《加法原理与乘法原理》兴趣篇的第10题，看起来平平无奇，答案就是标数法做的，老师也是这么讲。当标数法教完了，你可以画一个10×20的格子，然后让孩子去标，只要是正常的孩子都是拒绝的。

4年级导引上第11讲《加法原理与乘法原理》

那么我们来重新审视这道题目，其实完全可以用组合来做，从A到B为了保持最短路径必须要走8步，那么就是8个位置，我们选3个向上的位置，或者选5个向右的位置即可，那么就是C(8,3)或者C(8,5)。

问题还没有结束，接下来做一个变形，如果要求不能连续两步往上走怎么办。这个问题和上一个的区别就是8个步骤里面，向上的3步要分开，解决这种分割的方法就是插空法，相当于在6个空隙里面插进向上的3步，也就是C(6,3)。

这个时候可以往前看，回顾一下3年级导引第14讲《枚举法二》拓展篇第14题。当时没学排列组合，所以用的是树形图，那么既然我们已经学习了，那么可以试着做一下，按照横3竖0和横1竖2的情况分别求一下。枚举要花5分钟，排列组合不超过半分钟，这就是用高级方法降维的优势。

3年级导引第14讲《枚举法二》

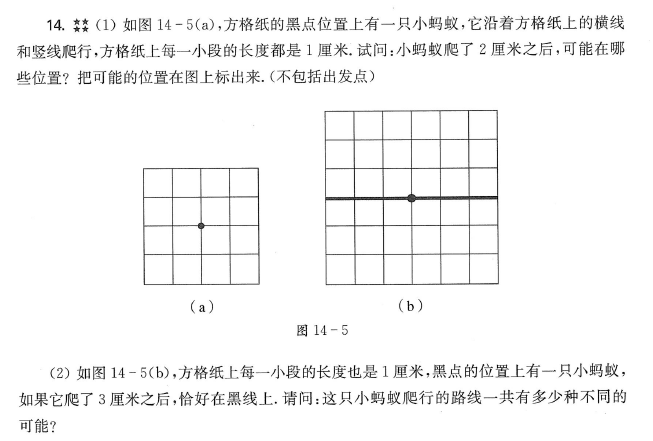
下面这道题目同样出自4年级导引第11讲《加法原理与乘法原理》超越篇，这道题目答案依然用了标数法。其实求一下总量，然后再减去必须经过黑点的路线即可，而经过黑点就是分为从A到黑点以及从黑点到B两步，所以我们用3个组合数就做出来了，也就是C(9,4)-C(5,2)×C(4,2)=66，和挨个标数相比，组合不仅省时间，而且正确率要高很多。

4年级导引上第11讲《加法原理与乘法原理》

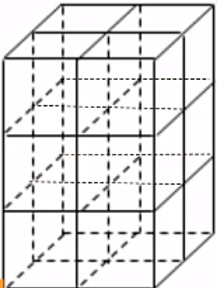
接下来，把问题再进行拓展，将题目拓展到三维空间里面，求这道题目里面从左下角到右上角最短路径有多少条。在三维空间里面标数是一个极其痛苦的事情（6年级大白本里面就有这种变态题目），不过用排列组合就轻松多了，依然半分钟解决，当然还可以再添加限制条件去拓展，和前面思路一样。

然后接着做下面这道5年级大白本第15讲《排列组合》第13题，解法也完全一样。这里多说几句，这道题目的解析是用排列做的，思路比较绕，计算也繁琐。其实可以这样理解，我一共需要9步，每条线互不影响，所以我只要在9步里面选2个位置给第一条线就可以，再在剩下的7步里面选3个给第二条，因为已经定序，所以是组合而非排列，也就是C(9,2)×C(7,3)=1260。比答案的先排列再消序要更接近本质，虽然计算结果上一样。

5年级大白本第15讲《排列组合》第13题

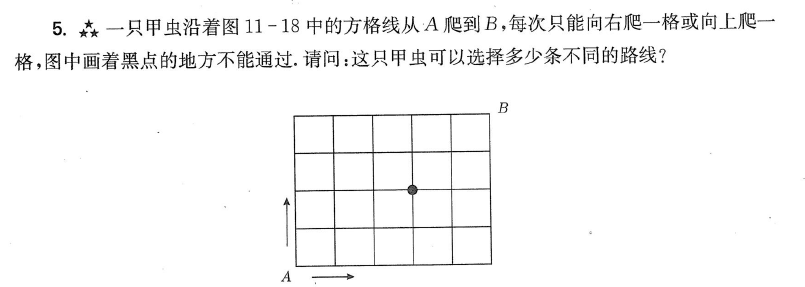
到这个时候的结论是就是组合比标数法要高级吗，当然不是，然后让孩子总结，什么时候用组合方法方便，什么时候用标数法方便。一般情况下，限制条件少的话，用组合正确率高，因为标数时候很可能手一抖就标错了。而在解决条件特别苛刻的时候标数法比较好用，因为限制条件越多，枚举量就越小。

接下来就要看一下标数法的优势，下面看5年级导引第22讲《计数综合二》拓展篇第13题，这道题目只有四个位置，那么答案利用加乘原理很容易算出答案。不过，这道题目可以引出一个计数里面非常重要的方法“阶梯标数法”。因为对于位置开始有要求，不过这个方法在这道题目里面并不能发挥优势。需要补充大白本题目。

5年级导引第22讲《计数综合二》

下面这两道题目，都是出自6年级大白本第11讲《计数综合二》，这就是阶梯标数法的典型应用。这两道题目利用分类讨论也能做，不过略显复杂。接下来可以总结一下阶梯标数法的应用场景：在处理对于大小或者先后有要求的计数问题。

6年级大白本第11讲《计数综合二》

在前面两道题目做完以后，可以做一下6年级导引13讲《计数综合四》超越篇第6题，也是这种做法。

6年级导引13讲《计数综合四》

以上这个案例，从一道简单的2星题开始，到了5星题结束。通过10道题目回顾了排列组合和标数法，虽然跨度是3-6年级的导引和5-6年级的大白本，但没有任何一个知识点是超纲和无法理解的，时间总花费为2小时左右。其他知识点也可以参考这个方式。

回顾一下就会发现，出题人给你画了一个标数法的网格，反而是组合更简单。而感觉要用排列组合的题目，更简单的反而是标数法。当你真正去研究的时候，会发现一道题目可以变成很多道题目，很多题目其实就是一道题目。只是在不同的情况下要用不同的方法而已。如果你在做完题困惑于为什么我想不到这种方法呢？想不到就是因为没有理解，没有和命题人产生共鸣。

还比如，可以把导引里面的行程问题都尝试能否用柳卡图来做，不一定全能做出来，但是能做出来的题目，可能会发现简单很多。比如下面6年级导引第14讲《行程问题六》超越篇这道题目，答案占用了一页纸，篇幅非常长，如果用S-T图来表示，过程会简洁很多。

6年级导引第14讲《行程问题六》

总结

很多孩子的问题在于上了很多课，做了太多题，学了太多的方法，而老师在教他们的时候。只说了这个方法怎么用，却没有说清楚为什么这么用，有什么局限性，还有没有其他方法，所以面对难题的时候，空有一身武功无处施展。

学习是先做加法再做减法的过程，做加法就是不断学习各种技巧，而研究导引就是在做减法，减去个性保留共性。很多高手都说做题没有什么技巧，其实他们都是经过了严格的技巧练习。减到最后剩下的就是解题的“感觉”，这种“感觉”无法描述，却又无处不在。