[数学] 2023 年第十届鹏程杯6年级数学邀请赛

不定项选择题
(本试卷满分 150 分,共 30 题,每小题 5 分。每题给出的五个选项中,至少有一 个正确答案,多选、错选、不选均不得分。少选且正确的,分值在正确选择中平均分配。)
❝1、计算:
A、21
B、25
C、24
D、23
E、31
❞
「答案解析」
此题没什么规律,将假分数统一成真分数,将除法转换成乘法后,依次死算即可。
选D。
❝2、有一群小朋友分一堆苹果,如果每人分
5个,就会剩下3个苹果。然后走了3个小朋友,此时每人分6个还是剩3个苹果,那么原来苹果的个数是( )A、93
B、90
C、68
D、64
E、15
❞
「答案解析」
走了3个小朋友,那原来分给这三个人的苹果有5x3=15个。
由于每人只多分了1个,因此现在的人数是15个人。
因此,总苹果数就是个。
选A。
由于这是选择题,由于苹果数可以写成:
满足条件的也只有A。
也可以设未知数,譬如设苹果数为x个,则有:
从而可以解得:
或者设小朋友y人:
化简:
所以,。
所以,苹果数就是个。
❝3、分数中,最大的是( )。
A、
B、
C、
D、
E、
❞
「答案解析」
以0.5为界,很明显,排除A和C。
由于分母的公倍数都比较大,我们尽量统一分子。
排除D。
而:
因此,选E。
❝4、鹏在书市上买了数学、童话、英语书共
7册。其中童活书、英语书都比数学书多,鹏鹏买了数学书( )。A、2
B、1
C、3
D、4
E、5
❞
「答案解析」
依题意,由于:
如果数学书有两本,则只能
不满足条件。
选B。
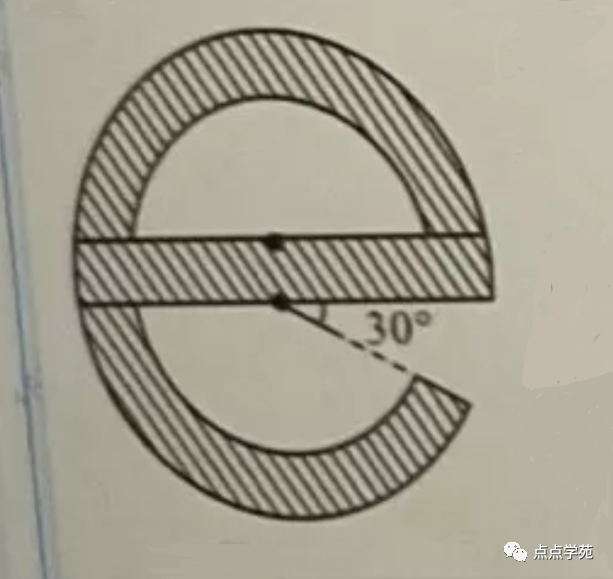
❝5、
IE浏览器的图标是字母e,图中e形的宽度是1cm,半圆及扇形的圆心均在长方形的边上,如果长方形的长为9cm,加么,e字形(阴影部分)的面积是( )平方厘米。(圆周率取3)
图5 A、60
B、50
C、41
D、31
E、22
❞
「答案解析」
所求面积为残缺圆环面积加上长方形面积:
选D。
❝6、一个最简真分数,分子、分母各加上另一个相同的分数后,所得分数与原分数相比较,则( )。
A、所得分数<原分数
B、所得分数≤原分数
C、所得分数>原分数
D、所得分数≥原分数
E、无法确定所得分数与原分数的大小关系
❞
「答案解析」
这里如果考虑分子为0的零分数,则所得分数和原分数相等。
否则,所得分数肯定比原数大。
由于是不定项选择题,那么C也是正确的。
选CD。
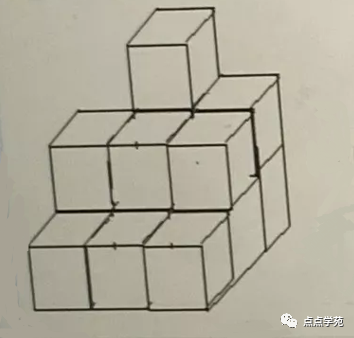
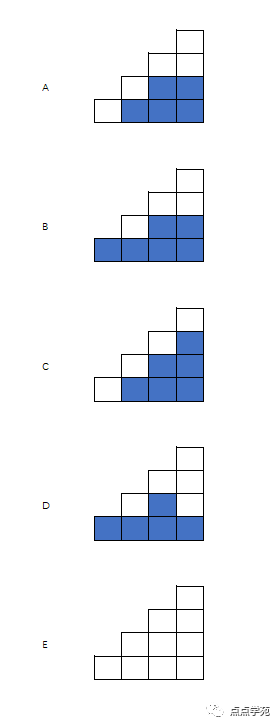
❝7、如图所示的立体图形由
14至16个棱长为1厘米的立方块搭成,这个立体图形的表面积(不记底面)至少为( )平方厘米。
图7 A、31
B、32
C、34
D、35
E、38
❞
「答案解析」
幸好是求表面积而不是体积。
依题意,考虑到支撑性,如果最下一层只有8个立方体,中间一层只有4个立方体,那总共只有13个立方体,不符合题意。
因此,最下一层有9个立方体,中间一层有4个立方体,加上最上面的一个,一共有9+4+1=14个。
最下一层外围一周有3x4=12平方厘米。
中间一层外围一周有(3+2)x2=10平方厘米。
最上一层外围一周有4平方厘米。
从俯视图看,表面面积有9平方厘米。
因此,该立方体表面积有:
选D。
❝8、
10口10口10口10口10的四个口中分别入加、减、乘、除运算符号,每种只填一次,不得另添加括号,则所成算式的最大值是( )。A、104
B、109
C、114
D、119
E、C和D不对
❞
「答案解析」
要想取最大值,减去的数必须最小,最小只能是1。
因此,该数是:
选BE。
❝9、小明从家到学校,走了
10分钟后,离学校还有20米,如果姐姐每分钟比他多走30米,她从家去学校走了7分钟后,离学校还有260米,那么小明家距离学校( )米。A、1760
B、1730
C、1500
D、1540
E、1520
❞
「答案解析」
姐姐和小明走了7分钟后,姐姐比小明多走了:
此时,小明距离学校:
因此,在分钟内,小明可以走:
因此,小明的速度就是:
因此,小明家距离学校:
选E。
❝10、黑球、红球和白球共2023个,如果黑球数比白球数多一倍,红球数比黑球数多
223个,求红球数有( )个。A、1760
B、1730
C、943
D、760
E、750
❞
「答案解析」
设白球数为x个,有:
解得:
所以,红球数是:
选C。
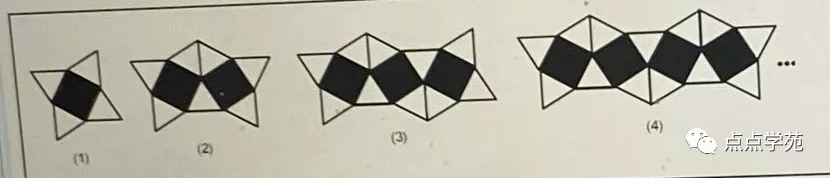
❝11、下图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成。照此规律,第
2023个图案有( )个三角形。
图11 A、606
B、4047
C、2024
D、6070
E、2023
❞
「答案解析」
我们先找找规律:
这里可以用动态规划的思想。
我们考虑第n-1个正方形,可以发现,按此规律再增加一个正方形到第n个,则三角形多了3个。
所以,我们可以总结出如下通项公式:
所以,当n=2023时,。
选D。
❝12、采茶姑娘每天上山采茶,上山每小时行
0.7千米,下山每小时行2.1千米,一天,她从山脚走到山顶,再从山顶原路返回到山脚,共用去6小时,她的平均速度是每小时( )米。A、800
B、900
C、1050
D、1010
E、1400
❞
「答案解析」
上山和下山的速度比是,则耗时比是,
因此,上山耗时为:
所以,平均速度就是:
另外也可用方程解答。
设距离为s,有:
所以:
所以,平均速度就是:
选C。
❝13、有一列数:
1,1,2,3,5,8,13,21,34,55,89,….。它的构成规律是:前两个数分别是
1;第
3个数等于第1个与第2个数之和:1+1=2;第
4个数等于第2个与第3个数之和:1+2=3;第
5个数等于第3个与第4个数之和:2+3=5;第
6个数等于第4个与第5个数之和:3+5=8;依次类推,这列数中的第
2023个数被7除的余数是( )。A、6
B、5
C、4
D、3
E、2
❞
「答案解析」
这里我们必须知道,两个形如7a+m和7b+n的数,其和除以7的余数等价于余数和除以7的余数。
针对余数,我们通过死算找规律,依次将规律写下来:
我们可以发现其每16个一循环,由于:
因此,第2023个数和第7个相同,第7个数是:
因此,其被7除的余数就是6,选A。
❝14、P、Q 是三角形ABC内2 个点,以P、Q、A、B、C为顶点,连出一些相瓦之间没有重叠的三角形,则这些三角形所有内角的和最大可以等于( )度。
A、360
B、180
C、540
D、720
E、900
❞
「答案解析」
最多只能构建出5个没有重叠的三角形,
因此,内角和可以是180x5=900度。
选E。
❝15、某项活动,要从甲、乙、丙、丁四个人中选出两个人参加,规定:
①如果选甲,那么也选乙;
②如果不选丙,那么也不选乙;
③如果选丙,则不选丁去。
那么,最后选出参加活动的两个人是()
A、甲
B、乙
C、丙
D、丁
E、以上都不对
❞
「答案解析」
如果条件①成立,则去的人是丙和丁,和条件③冲突,所以,甲没有参加。
如果条件②成立,去的是甲和丁,和条件①冲突,所以,丙有参加。
如果条件③成立,丙参加,丁没有参加。为了满足条件①,那么乙必须参加。
所以,参加活动的两个人是乙和丙。
选BC。
❝16、从
1开始把自然数依次写下去,得到:12345678910111213141516...,从第12个数字起,首次出现3个连排的1,那么从第( )个数字起将首次出现5个连排的2。A、555
B、558
C、562
D、559
E、556
❞
「答案解析」
首次出现5个连排的2,只能是222和223。
我们分类讨论下:
1)从1~9,共9个数字。
2)从10~99,共90x2=180个数字。
3)从100~199,共100x3=300个数字。
4)从200~221,共22x3=66个数字。
所以,所求数字位置为:
选E。
❝17、父亲与儿子的年龄和为 64,当儿子跟父亲一样大时,父亲已经 77,儿子今年( )岁。
A、18
B、17
C、16
D、15
E、19
❞
「答案解析」
如图所示:
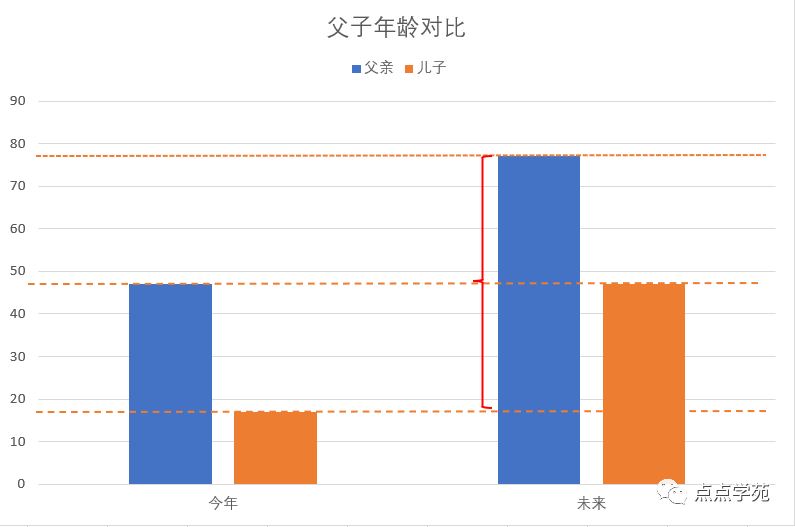
可以看到,77岁的父亲跟今年的儿子,年龄差了两个年龄差。
我们设年龄差为x,则今年儿子的年龄为:
那么,有等量关系:
解得:
所以,今年儿子的年龄就是:
选B。
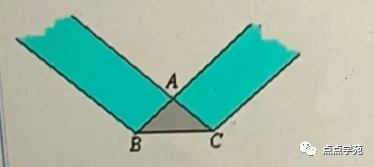
❝18、一条两边平行的纸带,纸带的宽度(两平行线间的距离)为
8厘米,将纸带折起压平。如图所示,则重叠部分三角形ABC的面积的最小值是( )平方厘米。
图18 A、56
B、32
C、64
D、50
E、33
❞
「答案解析」
这个题目看起来很不好算,但由于B选项中的数值最小,并且当∠ABC=45°时,三角形面积恰好就是:
因此,可以不需要要中学的知识去计算了。
选B。
假设我们所折角度为θ(就是图中点A位置的锐角)。
则:
所以,所求面积为:
当θ=90°时最小。
这属于三角函数,可以参考下思路。
选B。
❝19、己知甲管单独注满水池需要
30小时,乙管单独注满水池需要40小时,现在用甲管单独往水池中注水、在10小时后甲管出现故障,注水速度下降,此时如果将乙管打开,两管同时往水池中注水,16小时后可以注满水池。如果不打开乙管,则还需要( )小时才能注满。A、40
B、30
C、20
D、50
E、40.5
❞
「答案解析」
10小时后,水池还待注入的水有:
此时甲管速度降低,和乙管一起注水16小时,甲管的效率为两者效率和减去乙管的效率:
因此,如果不开乙管,甲管单独注水还需要:
选A。
❝20、二人分别从
A,B两地同时出发,相向而行,甲的速度是每分钟80米,乙的速度是60米,二人相遇后继续行进,甲到达B地和乙到达A地后都立即沿原路返回。已知两人再次相遇的地点距第一次相遇的地点300米,则A,B两地相距( )米。A、700
B、1050
C、265178
D、178526
E、不存在
❞
「答案解析」
这C和D里的数字好奇怪,第一感觉就想排除掉。
由于甲乙速度之比为:
那我们将AB两地距离分成7份。
第一次相遇时,甲走了4份,乙走了3份。
当甲到达B地的时候,乙往A地走了份。
当乙到达A地的时候,乙又走了份,此时甲往回走了份。
此时,甲乙相距为原有距离的份。
因此,再次相遇时,乙走了份。
两次相遇的距离为份。
因此,AB两地相距:
选B。
❝21、下图中,涂阴影部分的小的正六角星形面积是
16平方厘米,大正六角星形面积是( )平方厘米。
图21-1 A、24
B、12
C、32
D、64
E、48
❞
「答案解析」
如图所示:
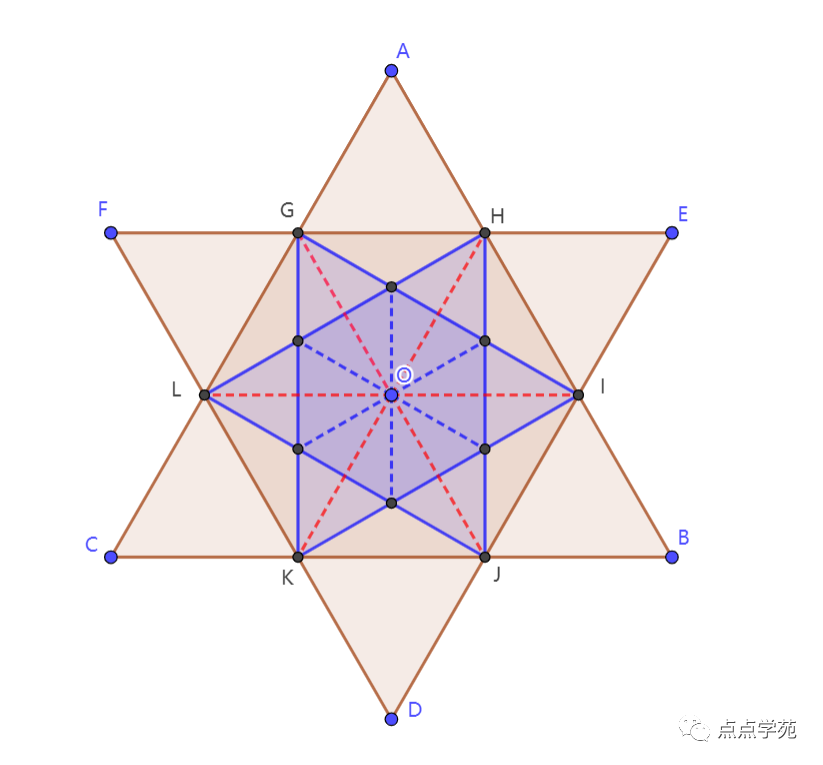
大正六角星和小正六角星都由12个等边三角形组成,可以看到,大等边三角形是小等边三角形面积的3倍。
因此,大六角星是小六角星面积的3倍。
因此,所求面积为平方厘米。
选E。
❝22、两地相距
999千米,沿路设有标志着距甲地及乙地的里程碑(如001|998),那么,有( )里程碑上只有两个不同数字。(注意,
000|999上只有两个不同的数字0和9; 而里程碑上001|998有4个不同的数字0,1,8,9)A、20
B、40
C、60
D、80
E、100
❞
「答案解析」
从十个数字中可以挑出5组数字,每组的数字和是9。
譬如0+9、1+8、2+7、3+6、4+5,注意,这里不考虑顺序。
对于0+9的组合,满足要求的里程碑有:
000|999、009|990、090|909、900|099、099|900、909|090、990|009、999|000,
共8组。
其他的可能性就没有了,一共就是5x8=40组。
选B。
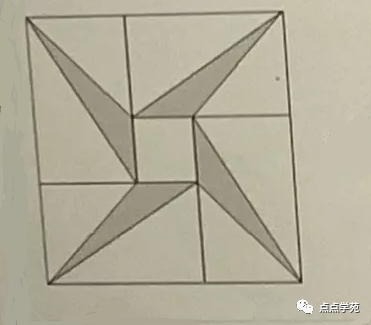
❝23、在下图,四张完全相同的长方形和一个面积为
4平方厘米的小正方形,拼成了一个大正方形,图中的阴影部分“风车形”的面积是20平方厘米,则大正方形的面积是( )平方厘米。
图23 A、144
B、122
C、132
D、164
E、120
❞
「答案解析」
小正方形面积是4,则其边长为2。
由于”风车“由4个三角形组成,因此,每个三角形面积是:
所以,三角形的高就是:
小长方形的长就是
大正方形的边长就是:
因此,其面积就是:
选A。
❝24、下面等式中,每个汉字表示
0~9中的一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么代表的六位数为( )A、935187
B、945189
C、784196
D、857142
E、以上都不对
❞
「答案解析」
可以不去死算,可以看到是的倍数,可以确认该数只能小于10。
因此,“超”为2,“常”为0,”鹏“为1,其他的数我们用字母来代替下:
1)如果a=9,那么b=7,有:
从而:
用了的数字有0,1,2,7,9 剩下可用的数字有:3,4,5,6,8
那么,要么:
分别验算下,e=6,d=4,c=8符合要求,也就是:
所求数就是784196。
2)如果a=8,那么b=9,有:
从而:
那么,d只能为5。
用了的数字有:0,1,2,5,8,9,剩下可用的数字有3,4,6,7。
那么,可以有:
经验算,符合要求,也就是:
所求数就是935187。
3)如果a=7,那么分数就是6,由于170x6=1020不是三位数,无解。
综上所述,只有上面这两种情况。
选AC。
❝25、下图是一个三角形数阵,其中数阵两侧的数比上一行大1,里面的每一个数都是它上一行与之相邻的两个数的和,这个数阵的前 8 行的和除以7的余数是( )。
A、0
B、2
C、4
D、6
E、以上都不对
❞
「答案解析」
我们将前8行补全:
我们依次写下每行之和除以7的余数,也就是:
选C。
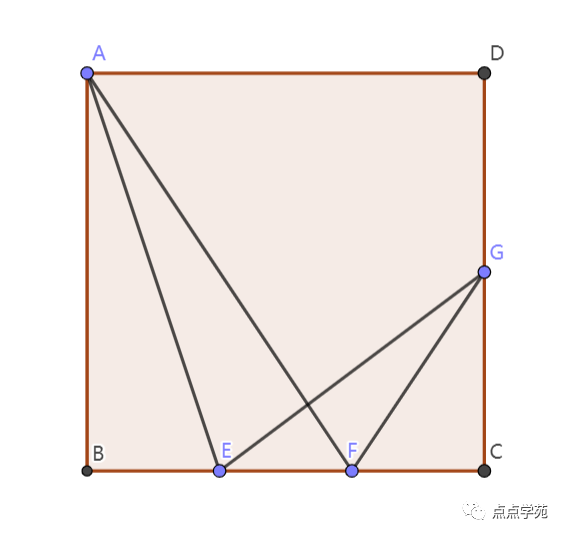
❝26、下图中,
ABCD是一个正方形,E,F是BC上的点,BE=EF=FC,G是CD上的中点,AF与EG交于H。已知正方形ABCD的面积是180平方厘米,则三角形AEH的面积比三角形HFG的面积大( )平方厘米。
图26-1 A、20
B、25
C、30
D、15
E、10
❞
「答案解析」
如图,连接AG。
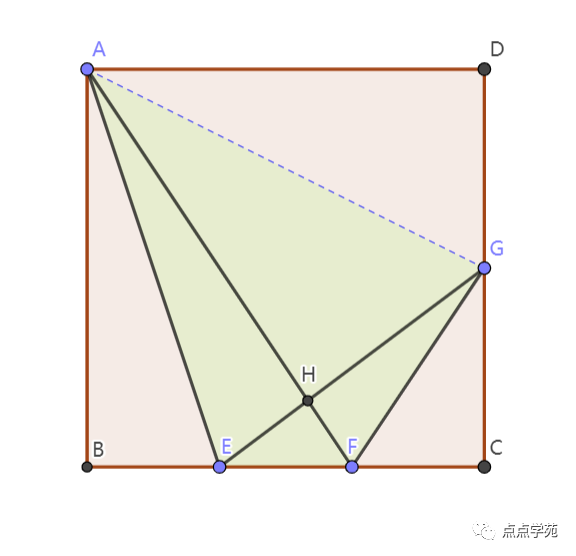
根据等底等高之类的原理,有:
所以:
选D。
当然,也可以傻傻地继续算下去。
所以:
考虑三角形AEG和EFG共高的关系,所以有:
同理,三角形AEH和EHF也共高,所以有:
考虑三角形AFG和AEF共高的关系,所以有:
同理,三角形AFG和AEF也共高,所以有:
所以,三角形AEH的面积比三角形 HFG的面积多25-10=15平方厘米。
❝27、下列6个图形分别表示 1~6,注意观察小球的数量与位置,那么表示
66的是( )。
图27-1
图27-2 E选项不全,不确定是什么样的了,权且用蓝色来代替球+脑补。
❞
「答案解析」
直觉是参考二进制的表示,但数字6的表示却发生了突变。
感觉信息不够,1~5有规律可循,譬如第一列每格代表1、第二列每格代表2。
那如果第三列每格代表6,那第4列每格代表几呢?
由于66是偶数,B跟D第一格都有,排除B和D。
❝28、用方格纸剪成面积为4 的图形,其形状只能有以下7种。如果用其中的四种拼成一个面积为16 的正方形,且这四种图形的标号之和为最小,那么应选( )。
图28-1 A、①⑤⑥⑦
B、①③⑤⑦
C、①②③⑥
D、①②③⑦
E、②③④⑤
❞
「答案解析」
仔细观察题目,从答案中猜测,①是可以用上的,为了使标号和最小,我们尽量也将②用上。
那么,我们只要将C或D排出来,那其他的就不用尝试了。
从标号之和也可以看出来,C最小,D其次。
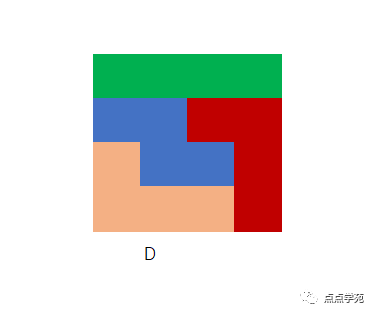
很明显,我们可以将D排出来,那么除了C之外,其他三种就不用再考虑了。
尝试排列了下,发现C是不可能实现的。
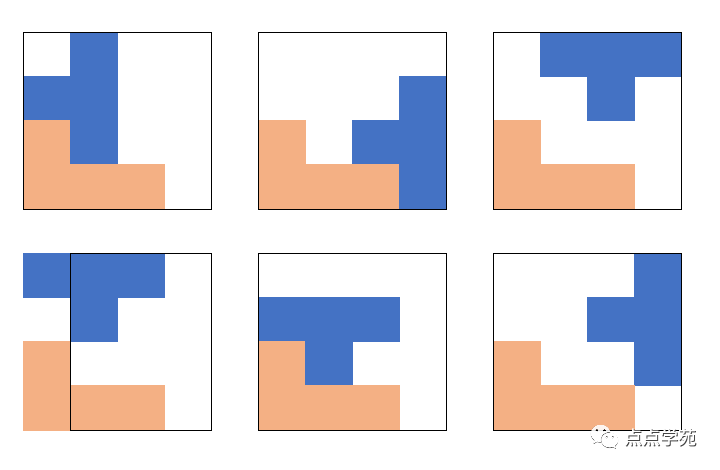
选D。
❝29、有一批长度分别为
2、5、6、7、10和11厘米的细木条,它们的数量都足够多。从中选取3根木条作为三条边,可围成一个三角形。这些木条共能围成( )种不同的三角形。A、41
B、30
C、20
D、12
E、以上都不对
❞
「答案解析」
我们先分类,再枚举,最后累加。
「1)」如果每条边都不相等。
以最短边入手。
1.1)最短边长为2
共2,5,6、2,6,7、2,10,11三种。
1.2)最短边长为5
共5,6,7、5,6,10、5,7,10、5,7,11、5,10,11五种。
1.3)最短边长为6
共6,7,10、6,7,11、6,10,11三种。
1.4)最短边长为7
共7,10,11一种。
这样一共就有3+5+3+1=12种。
「2)」如果每条边都相等。
那么就有6种。
「3)」如果只有两条边相等。
也从最短边入手。
3.1)最短边长为2
有2,5,5、2,6,6、2,7,7、2,10,10、2,11,11共5种。
3.2)最短边长为5
有5,5,6、5,6,6、5,7,7、5,5,7、5,10,10、5,11,11共6种。
3.3)最短边长为6
有6,6,7、6,7,7、6,10,10、6,6,10、6,6,11、6,11,11共6种。
3.4)最短边长为7
有7,7,10、7,10,10、7,7,11、7,11,11共4种。
3.5)最短边长为10
有10,10,11、10,11,11共2种。
可以看到,有
综上所述,一共有:
选A。
❝30、从自然数
1至25中任意取出k个数,要求其中必有2个,较大者是较小者的2倍,则k的最小值是( )。A、18
B、17
C、19
D、20
E、21
❞
「答案解析」
先考虑最极端情况。
譬如取出的数刚好是13~25这13个数,这里彼此之间不存在2的倍数。
由于13比较大,那么很明显,1、3、4、5也符合要求。
那么,得到的集合就是:
在这个集合中,一共17个数,彼此之间不存在2倍关系。
但如果再从其他数中再挑一个,就存在了2倍关系。
譬如,2和4、6和3、7和14、8和16、9和18、10和20、11和22、12和6,24。
因此,最小值是17+1=18个。
那就排除C、D、E。
很明显选A。
暂时选。但估计答案是没有提供正确答案(此行删除)。

① 华杯赛/华数之星真题试卷-解析版 附详细解题过程
② 迎春杯/青少年创新能力测试-解析版 附详细解题过程
③ 希望杯/希望数学-解析版 附详细解题过程
④ YMO世界青少年奥林匹克数学竞赛-解析版 附详细解题过程
⑦ 美国数学大联盟杯-解析版 附详细解题过程
⑧ 鹏程杯-解析版 附详细解题过程
⑨ 历年全国小数测初评、终评真题及答案解析
② 朗思 iESOL 备考资料
② 深圳小学各科上/下学期单元测试、期末真题及答案解析
② 深圳初中入学测试、月考、期末真题及答案解析(上、下学期)
② 深圳高中各科入学测试、月考、期末真题及答案解析
添加 家长论坛微信



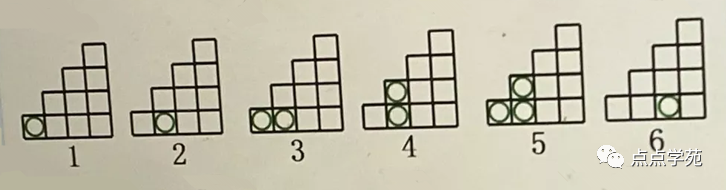


全部 0条评论