1.  完全二叉树的权值(2019年试题 G)

【问题描述】
给定一棵包含N个节点的完全二叉树，树上的每个节点都有一个权值，按从上到下、从左到右的顺序依次是A₁,A₂,A₃……A_N，如下图1所示。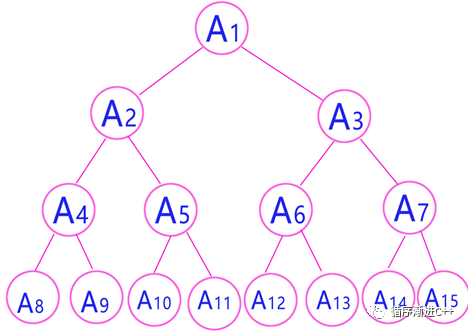
图1
现在，小明要把相同深度的节点的权值加到一起 ，他想知道哪个深度的节点权值之和最大。如果有多个深度的权值和都是最大值，则输出其中最小的深度。
注意:根的深度是1。
[输入格式]
第一行包含一个整数N。
第二行包含N个整数A₁,A₂,A₃……A_N。
[输出格式]
输出一个整数，代表答案。
[样例输入]
7
1 6 5 4 3 2 1
[样例输出]
2
[评测用例规模与约定]
对于所有评测用例,1≤N≤100000，-100000≤Ai≤100000 

[提示]

本题并无特殊技巧，对每一层进行遍历并对每一层的权值求和，比较出最大值即可。需要注意完全二叉树的顺序存储和数组下标的关系。

2. 等差数列(2019年试题 H)

【问题描述】
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了其中数列的一部分，只记得其中有N个整数。现在给出这N个整数，小明想知道包含这N个整数的最短的等差数列有几项?
[输入格式]
第一行包含一个整数N。
第二行包含N个整数A₁,A₂,A₃……A_N。(注意: A₁,A₂,A₃……A_N并不一定是按等差数列中的顺序给出的)。
[输出格式]
输出一个整数，表示答案。
[样例输入]
2   6  4  10  20
[样例输出]
10
[样例说明]
包含2、6、4、10、20 的最短的等差数列是2、4、6、8、10、12、14、16、18、20。
[评测用例规模与约定]
对于所有评测用例,2≤N≤100000,0≤Ai≤109。
[提示]
（1）本题的解题方法相对比较容易想到，首先对原始数列进行排序:
2  4  6  10  20
（2）然后按顺序求出相邻两个数之间的差:
2  2  4   10
（3）接着求所有差的最大公约数:
2 （4）最后利用公差的项数公式，计算项数。

3.上期答案——数的分解

【参考程序1】——宋秀杰答案

#include <stdio.h>
int isOk(int a)//判断是数字是否有2或4 
{
 int b;
 while(a){
  b=a%10;
  if(b==2||b==4)
  return 0;
  a/=10;
 }
 return 1;
}
int main()
{
int a=2019,count=0,i,j,k;
  for(i=1;i<673;i++)
    for(j=i+1;j<1009;j++) 
     for(k=j+1;k<2017;k++){
       if(i+j+k==2019&&isOk(i)&&isOk(j)&&isOk(k))
        count++; 
       }
printf("%d",count);
return 0;
}

【参考程序2】——吴炳毅答案（这个答案用了对所有数的枚举，三个数据的全排列是6种，最后用总的序列除以6，效率虽然低些，但是思路没有问题，结果也正确）

#include <iostream>
using namespace std;
int A(int a){
    int b=0;
while(a){
if(a%10==2||a%10==4)b++;
a=a/10;
}
if(b==0)return 1;
else return 0;
}
int main(int argc, char** argv) {
int a=2019;
int num=0;
for(int i=1;i<a;i++){
for(int j=1;j<a;j++){
int b=a-i-j;
if(b>0&&A(i)&&A(j)&&A(b)&&i!=j&&j!=b&&b!=i) num++;
}
}
num/=6;
cout<<num;
}

4.上期答案——特别数之和

（这个题目简单，都是一个思路）

【参考程序2】

# include<iostream>
using namespace std;
bool isOk(int n) //整数n是否满足条件
{
 while(n)
 {
 if(n%10==2||n%10==0||n%10==1||n%10==9)
       return true;
    n/=10;
    }
 return false;
}
int main()
{
 int n;
 int sum=0;
 cout<<"input n："; 
 cin>>n;
 for(int i=1;i<=n;i++)
  if(isOk(i))
   sum+= i;
 cout<<sum;
 return 0;
}

---

添加 家长论坛微信