蓝桥杯 | DFS算法及例题01,02
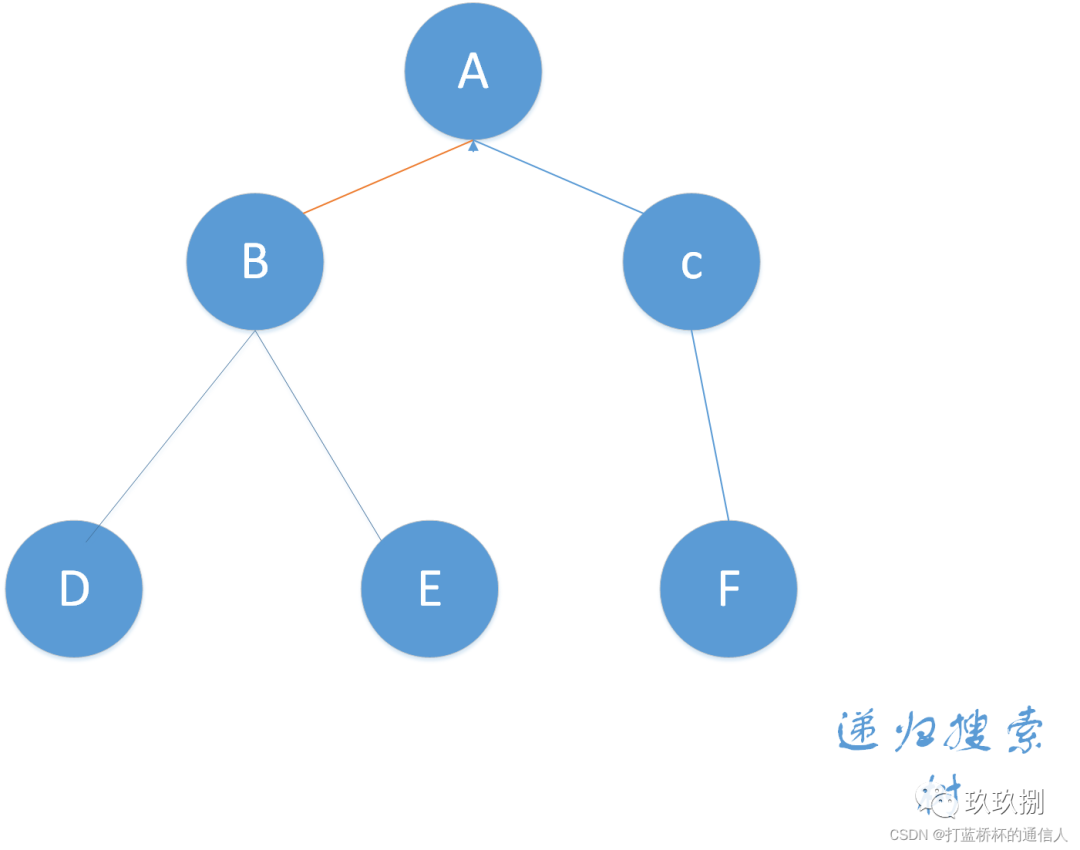
DFS模板:
#include <iostream>using namespace std;bool check(){...}void dfs(){if (满足边界条件){return;}for (int i = 0; i < 可扩展的路径数; i++){if (check()){修改现场;dfs(下一种情况);还原现场;}}}
经典DFS例题:
1.模板题——迷宫问题
题目介绍:
给定一个N*M方格的迷宫,迷宫内设置有T处障碍。给定起点坐标和终点坐标,问:每个方格最多经过一次,有多少种起点到终点的方案。在迷宫中有上下左右三种移动方式,且每次只能移动一格。
输入格式:
第一行输入N行,M列和T个障碍,第二行输入起点坐标SX,SY和终点坐标FX,FY,接下来T行,每行都为自定义的障碍物的坐标。
输出格式:
从起点坐标到终点坐标的方案总数
输入输出样例:
输入:
2 2 1
1 1 2 2
1 2
输出:
1
题目分析:
迷宫问题是拿来练习DFS和BFS的很经典的题目,迷宫问题有很多种问法,比如迷宫从起点到终点的路径有几条,最短路径是多少。
(个人:其实就是把每一步都走一遍,碰壁则回头重新开始,比如一棵大树,一根树枝一根树枝的遍历,减去不合理的枝干,所以时间复杂度会很高)
以数组map[][]来表示迷宫,当 map [ ] [ ] ==1 时为障碍点, map [ ] [ ] == 0时为正常点,设置好迷宫后开始遍历。
AC代码:
#include <iostream>using namespace std;const int N = 100;int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};//方向数组技巧int n, m, T;//n行m列T障碍总数int ans;//记录方案总数int sx, sy, fx, fy, l, r;//起点坐标(sx,sy)终点坐标(fx,fy)障碍点坐标(l,r)bool visited[N][N];//记录某点是否被访问过int map[N][N];//map[i][j] == 1表示是障碍bool check(int x, int y)//check某点是否合法{if (x < 1 || x > n || y < 1 || y > m) return false;//该点出界不合法if (map[x][y]) return false;//该点是障碍点不合法if (visited[x][y]) return false;//该点被访问过不合法return true;//其他情况访问合法}void dfs(int x, int y)//dfs维护点的坐标参数{if (x == fx && y == fy)//满足边界条件,到达终点{ans++;//方案数+1return;}for (int i = 0; i < 4; i++)//枚举四个方向{int newx = x + dx[i];int newy = y + dy[i];if (check(newx, newy))//该点合法{visited[x][y] = true;//将(x,y)设置成已访问,修改现场dfs(newx, newy);//dfs下一个点visited[x][y] = false;//回溯,恢复现场}}}int main(){cin >> n >> m >> T;cin >> sx >> sy >> fx >> fy;while(T--){cin >> l >> r;map[l][r] = 1;}dfs(sx, sy);//从起点开始搜索cout << ans << endl;return 0;}
空间优化,以maze数组表示迷宫,同时可以记录迷宫中的点是否被访问(可能是减少时间复杂度,避免超时)
//空间优化#include <iostream>using namespace std;const int N = 100;int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};//方向数组int n, m, T;int ans;int sx, sy, fx, fy, l, r;//bool visited[N][N];int map[N][N];//map[i][j] == 1表示是障碍bool check(int x, int y)//判断某点是否可以访问{if (x < 1 || x > n || y < 1 || y > n) return false;if (map[x][y] || map[x][y] == 3 ) return false;//该点是障碍点或已经访问过,不能访问//if (visited[x][y]) return false;return true;}void dfs(int x, int y){if (x == fx && y == fy){ans++;return;}for (int i = 0; i < 4; i++){int newx = x + dx[i];int newy = y + dy[i];if (check(newx, newy)){map[x][y] = 3;//标记成已访问dfs(newx, newy);//点(x,y)能访问说明它不是障碍点所以回溯要让map[x][y]=0//而不是map[x][y]=1map[x][y] = 0;}}}int main(){cin >> n >> m >> T;cin >> sx >> sy >> fx >> fy;while(T--){cin >> l >> r;map[l][r] = 1;}dfs(sx, sy);cout << ans << endl;return 0;}
2.01背包问题
题目分析:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是Vi,价值是Wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式:
第一行有两个整数,N ,V ,用空格隔开,分别表示物品数量和背包容积。
接下来用 N 行,每行两个整数Vi和Wi 分别代表第 i 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N , V <=1000
0<Vi , Wi <=1000
输入样例:
4 5
1 2
2 4
3 4
4 5
输出样例:
8
题目分析:
背包问题也是一个经典问题,有很多种解法,DFS就是其中一种。
第 i 件物品无非就是选和不选两种情况,在搜索的过程中DFS函数必须要记录当前处理的物品编号index,和当前背包的容量sumi,当前的总价值sumC
如果不选择第i个物品时,此时sumi,sumC的值不变,然后去判断第i+1个物品,也就是DFS(i,sumi,sumC)。
当选择第 i 个物品时,sum 变成 sumi+w[i] ,sumC变成sumC+v[ i ] ,接着处理第 i +1 个物品,也就是DFS(i+1,sumi+W[i],sumC+V[i]。边界条件也就是把最后的一件物品也处理完,即为当n=i的时候。
当一条分支结束时,需要判断该分支最终满不满足总重量不大于背包容量,即为 sumi<=v。满足的话则更新价值maxvaule 即 maxvalue=max(maxvalue,sumC)。
AC代码:
//01背包问题的dfs版本#include <iostream>#include <algorithm>using namespace std;const int N = 10010;int n, v, maxvalue;int w[N], c[N];//DFS维护三个参数,正在选第index个物品,当前的总体积,当前的总价值void dfs(int index, int sumW, int sumC){if (index == n){if (sumW <= v){maxvalue = max(maxvalue, sumC);}return;}dfs(index + 1, sumW, sumC);//不选第index个物品dfs(index + 1, sumW + w[index], sumC + c[index]);//选第index个物品}int main(){cin >> n >> v;for (int i = 0; i < n; i++){cin >> w[i] >> c[i];}dfs(0, 0, 0);//开始时对第1件物品进行选择,此时背包重量0价值也是0cout << maxvalue << endl;return 0;}
如果背包问题用DFS来解决,当数据比较大的时候仍然不能使用AC,会导致超出时间限制。

添加 家长论坛微信


全部 0条评论