揭秘三角形外心、垂心、重心之间的关系：数学奥林匹克小丛书--初中卷（5）
-
-
上海小升初 这家伙很懒，还没有设置简介
0 人点赞了该文章 · 153 浏览
本系列参考教材为小蓝本：数学奥林匹克小丛书（第三版）初中卷
正文
第七章 三角形的四心
除了它们各自的性质，将其中几个心组合起来又可得到一些美妙的性质，下面我们介绍两个定理：
卡诺定理
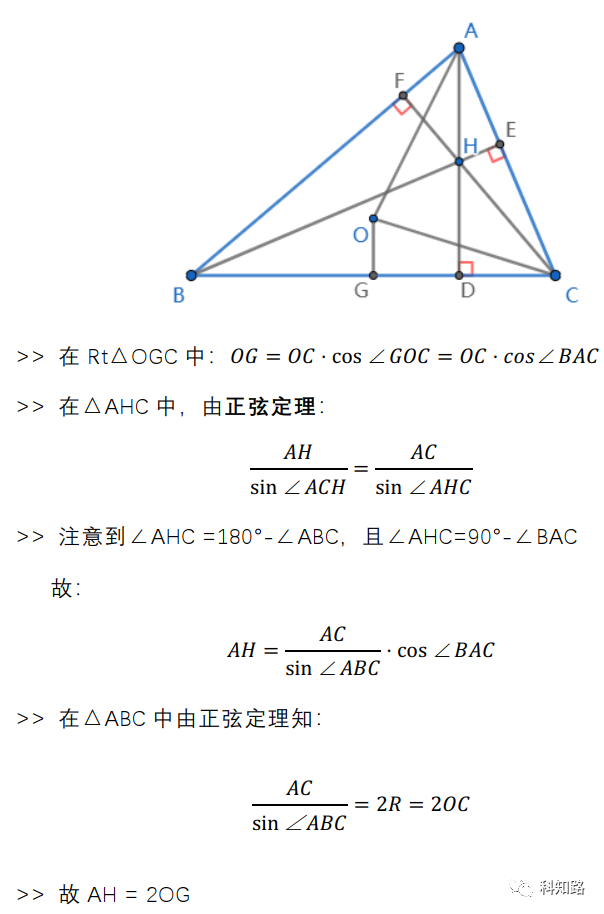
这个定理本身非常特别，揭示了外心和垂心之间的奇妙联系，下面我们尝试用多种方法进行证明，其中纯几何的证明以构造线段OG的二倍为入手点，借助中位线、平行四边形、直角三角形以及圆的知识完成证明。教材上的做法以中点构图为主，这里不再赘述。
证明思路一：
下面这一方法个人认为最为简单直接，比教材上的更容易想到：
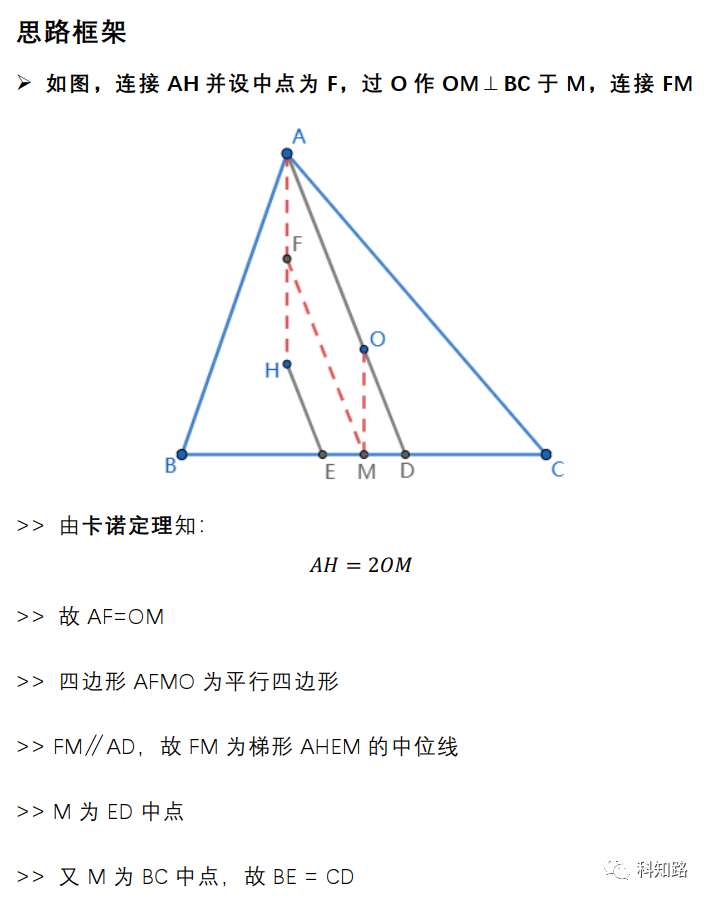
证明思路二：
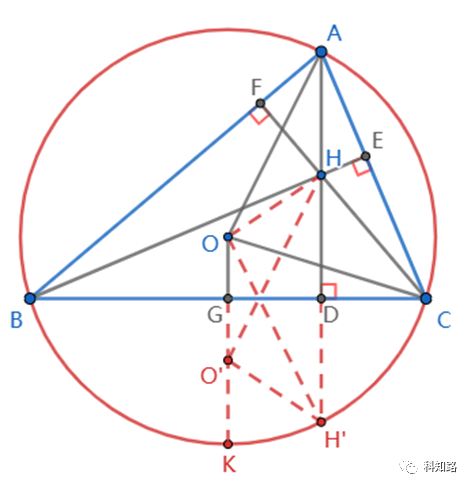
证明思路三：计算法（三角函数）
在卡诺定理基础上，我们可以进一步证明欧拉定理，得到外心、垂心和重心之间的关系：
欧拉定理
最后我们看一道例题：
本题利用卡诺定理很容易解决，只需要构造出对应的元素。
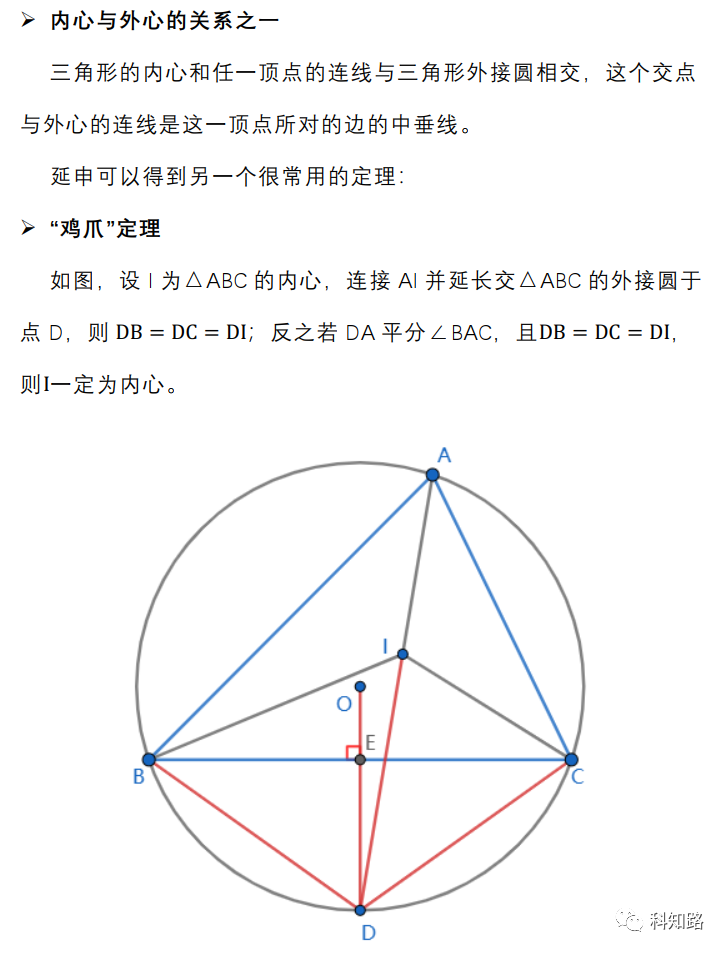
三角形任一顶点与外心、垂心的连线构成等角线
全部 0条评论