比利时弗拉芒区青少年数学奥林匹克竞赛（JWO）面向比利时弗拉芒大区（荷语区）中学3年级和4年级的学生。每年大约有1万多名选手参加第一轮的比赛，其中大约1千名选手晋级第二轮，通过两轮选择题的选拨，大约有70-80名选手最后晋级决赛。

JWO的决赛由四道开放式问题组成，与其他国家的青少年数学奥林匹克竞赛相比，其难度不高。大致相当于国内普通初中的练习题？

今年的JWO决赛于4月17日下午在布鲁塞尔大学进行。赛后我从小朋友手中拿到试题，下面对这四道题作一些分析和解答。

（看到试卷变成这个样子，我猜测这位小朋友一定在考试过程中把题目都掰开揉碎了理解，可以期待取得好成绩哦！）

第一题，简单翻译如下：

Christelle做了n ≥ 2个煎饼，这些煎饼大小各不相同，她把这些煎饼叠放在一个盘子上。Christelle希望这些煎饼可以由大到小叠放（最大的一个放在最下面），改变这些煎饼叠放顺序的唯一方法是将锅铲推入到某个煎饼的底下，然后通过翻转锅铲，把其上方的所有煎饼翻过来再叠放回盘子上。试证明：Christell最多需要翻转2n – 3次锅铲，就可以使得这一堆煎饼按照她所希望的顺序叠放。

分析：

解决问题最基本的一条黄金规则就是：从最简单的几种情况入手，然后分析这几种情况之间有何联系，是否存在递推的关系，再根据需要证明的问题是否和整数序列有关，从而考虑使用数学归纳法。

这道题就是适用于上述思路的一个典型例子。

解答：

对于n = 2的情况。

如果大煎饼在小煎饼之下，那么Christelle无须做什么翻转。

如果大煎饼在小煎饼之上，那么Christelle只需将锅铲推入小煎饼下方，进行一次翻转，即可使得两个煎饼按照由大到小的顺序叠放。

因此，对于n = 2，翻转次数最多1 = 2 ∙ 2 – 3次。

命题对于n = 2成立。

假设命题对于n = k成立，即对于一堆k个煎饼，最多只需2k – 3次翻转即可使得这k个煎饼按照由大到小的顺序叠放。

现在考虑以任意顺序叠放的k + 1个煎饼，我们可以通过以下操作将这k + 1个煎饼按照由大到小的顺序叠放。

1. 找到其中最大的一个煎饼，将锅铲推入其下方，将这个煎饼及其以上的所有煎饼翻转，此时最大的煎饼位于整个煎饼堆的最上方。

2. 将锅铲推入整个煎饼堆的下方，将所有煎饼翻转，此时最大的煎饼位于整个煎饼堆的最下方。

3. 考虑由除最大煎饼之外的k个煎饼组成的煎饼堆，根据假设，最多需要2k – 3次翻转即可使得它们以由大到小的顺序叠放。

通过以上最多1 + 1 + 2k – 3 = 2(k + 1) – 3 次翻转，以任意顺序叠放的k + 1个煎饼即可变成按照由大到小的顺序叠放。

因此，命题对于n = k +1也成立。

综上，根据数学归纳法，对于任意n ≥ 2，Christelle最多需要2n – 3次翻转即可使得这n个煎饼按照由大到小的顺序叠放。

证明完毕。

第二题，简单翻译如下：

Ron有一块只有白色格子的神奇游戏板，他希望将它制作成一个带有白色和黑色格子的象棋棋盘图案，图案中相同颜色的格子互不相邻。

此外，Ron还有一个棋子：一只马。Ron可以把这只马放置在他选好的格子中，然后通过马的跳跃将其移动到另一个格子。如旁边的图示，在每次跳跃中，马要么横向移动两个格子、纵向移动一个格子；要么横向移动一个格子，纵向移动两个格子。

在下面的俯视图中，马在跳跃中越过了两个格子，如图中的交叉标记所示。在马的任意一次跳跃中，这两个格子的颜色都随之发生一次转变：黑色的格子将变成白色，而白色的格子将变成黑色，如旁图中的例子所示。

试证明：

a. 当游戏板为3 × 3格子大小时，Ron可以将它转换成一个象棋棋盘图案。

b. 当游戏板为4 × 4格子大小时，Ron无法将它转换成一个象棋棋盘图案。

c. 当游戏板为3 × 5格子大小时，Ron无法将它转换成一个象棋棋盘图案。

分析：

这是一道以棋盘为背景的组合题，一般来说，可以先根据游戏规则，将棋盘中的格子分成几类，观察每类格子的数量，然后再通过计算每类格子的奇偶性、计算棋盘和覆盖形状之间的整除性、或者利用特殊的涂色方案证伪完美覆盖不可行。

这道题比较简单，大致用不到上面所说的后两种方法。

解答：

a. 证明可行，一般不需要啥技巧，阐述或者描述一种可行的方法就行。

对于3 × 3格子大小的游戏板，可以把其格子按照位置标记为3类：角上的格子C，边上的格子S和中央的格子M。

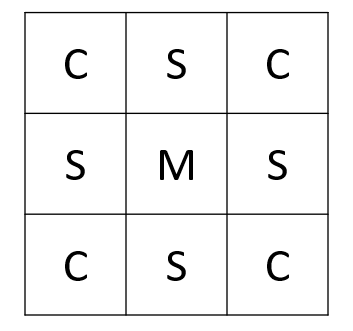
马在这样的格子间跳跃，显然只存在从C跳到S，或者从S跳到C的跳跃方式，无法从M起跳，也无法跳跃到M。

无论从C跳到S，还是从S跳到C，按照题目中的规则，越过的两个格子一定为一个S和一个C。从全部白色格子的游戏板，到黑白格子相间的象棋棋盘图案，最少需要将其中的四个格子变为黑色，所以至少需要4次跳跃。

而这4次跳跃是可行的，马按照下图所示的顺序跳跃即可。

b. 证明不可行，有时候比证明可行还要简单。

对于4 × 4格子大小的游戏板，用类似的方法根据格子位置的不同将它们分成C，S和M三类。

不难看出，根据题目中通过马的跳跃来改变颜色的规则，只有S和M的颜色可能被改变，而马不可能越过C，所以C的颜色将保持为白色。

假设4 × 4格子大小的游戏板最终可以转变为黑白格相间的图案，考虑第一行两个角上的方格C，它们之间相差3个格子为奇数，所以这两个格子的颜色互不相同，其中必然存在一个黑色格子。

这与上述C的颜色将保持为白色相矛盾。

因此，4 × 4格子大小的游戏板无法转变为一个象棋棋盘图案。

c. 同样使用反证法。

假设3 × 5格子大小的游戏板最终可以转变为黑白格相间的图案，根据b中得到的结论，其角上的格子只能是白色，所以最终图案只有下图这一种情况。

如果将白色格子数值记为0，黑色格子数值记为1，那么在游戏板的初始状态，全部15个格子都是白色，15个格子数值的总和为0，是个偶数；在最终的黑白格相间的图案中，一共有7个黑色格子，8个白色格子，15个格子数值的总和为7，是个奇数。

而在马的每一次跳跃中，有且只有两个格子的颜色发生改变，不论是从黑色变成白色还是从白色变成黑色，这两个格子数值的奇偶性同时发生变换，使得在跳跃后，这两个格子数值之和的奇偶性不变，所以所有15个格子数值总和的奇偶性也保持不变。

所以，不论跳跃多少次，也不论如何跳跃，这15个格子数值的总和不可能从初始状态的0变为最终黑白格相间图案状态的7。

因此，3 × 5格子大小的游戏板无法转变为一个象棋棋盘图案。

第三题，简单翻译如下：

如图所示，两个相同大小的圆相切，且每个圆都与一个直角三角形的两条边相切。已知直角三角形的两条直角边的边长分别为21和28，圆的半径是多少？

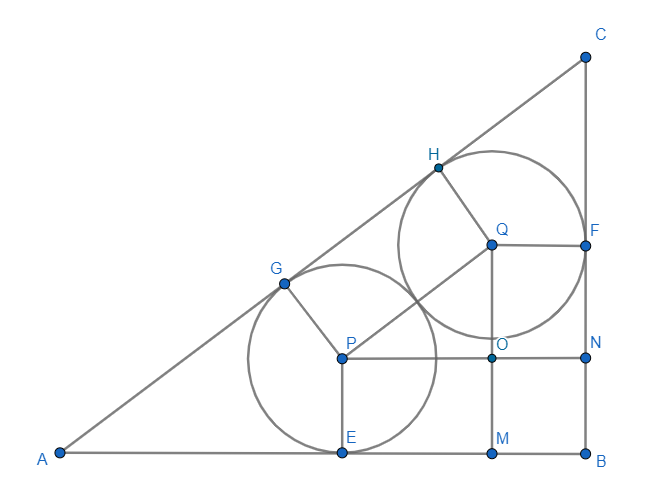
分析：

圆和圆相切，圆和三角形相切，一个简单的思路就是先把圆心和圆心连接起来，把圆心和切点连接起来，然后寻找直角三角形使用勾股定理。

解答：

令两圆的圆心分别为P和Q，圆的半径为r。

如图所示，令两圆和三角形边之间的切点分别为E、F、G、H。通过P作BC的垂线，垂足为N；通过Q作AB的垂线，垂足为M，PN交QM于O。

因为AB ⊥ CB，易知PN ⊥ QM。

再由相切关系，易知PQGH、POME、QONF都为矩形，BMON为边长为r的正方形。

因为∆POQ的三条边分别与∆ABC的三条边平行，所以

∠OPQ = ∠BAC，∠QPO = ∠CAB

所以，∆POQ ~ ∆ABC。

根据勾股定理，易知BC : AB : CA = 3 : 4 : 5，CA = 35。

所以，OQ : PO : QP = 3 : 4 : 5。

又QP = 2r，所以

PO = 2r/5 ∙ 4 = 8r/5，OQ = 2r/5 ∙ 3 = 6r/5。

这样，

GH = PQ = 2r，

EM = PO = 8r/5，

EN = QO = 6r/5。

由同一点引圆的两条切线，令AE = AG = a，CF = CH = c。

这样，

AB = 28 = a + 8r/5 + r

BC = 21 = c + 6r/5 + r

CA = 35 = a + c + 2r

前两式相加减去第三式，得到：14 = 14r/5。

所以，r = 5。

第四题，简单翻译如下：

设a₁, a₂, a₃, …, a₉为正实数，满足

a₁² + a₂² + a₃²+ … + a₉² ≤ 2024

试证明：在a₁, a₂, a₃, …, a₉这9个数字中存在3个数字，其和小于45。

分析：

题目的条件是一个轮换对称的不等式，证明的目标也是一个不等式，可以考虑使用基本的均值不等式。

解答：

利用反证法。

假设在a₁, a₂, a₃, …, a₉这9个数字中的任意3个数字之和都大于等于45，即

对于任意互不相等的1 ≤ i, j, k ≤ 9，都有a_i + a_j + a_k ≥ 45。

考虑从9个数字中选取3个数字的组合数C(9, 3) = 84，所以诸如

a_i + a_j + a_k ≥ 45

的不等式一共有84个。

将这84个不等式加起来，因为a₁, a₂, a₃, …, a₉中的每个数字在这84个不等式中出现3 ∙ 84 / 9 = 28次，所以加起来后的不等式即

28(a₁ + a₂ + a₃ + … + a₉) ≥ 45 ∙ 84

简化得到，

a₁ + a₂ + a₃ + … + a₉ ≥ 135

根据均值不等式中的AM-QM，有

(a₁ + a₂ + a₃ + … + a₉)/9 ≤ √[(a₁² + a₂² + a₃² + … + a₉²)/9]

综合以上两个不等式，有

135/9 ≤ √[(a₁² + a₂² + a₃² + … + a₉²)/9]

整理后，得到

a₁² + a₂² + a₃² + … + a₉² ≥ 135²/9 = 2025

这与题目中的条件a₁² + a₂² + a₃² + … + a₉² ≤ 2024相矛盾。

因此，在a₁, a₂, a₃, …, a₉这9个数字中必然存在3个数字，其和小于45。

证明完毕。