2024年中科大少年班入围数学试卷”。我大略看了看，感觉这张试卷更注重的是知识的广度，而不是挖掘所谓的“解题技巧”。毕竟只是入围题，以考查知识点为主很正常，难度并不大。如果考生的知识面拓展到了 多项式定理、复平面、定积分、图论、条件概率，等等，答起来就会比较容易。此外，还需要耐心和细心，不要错过细节。

下面我们挑选其中的第五题进行解析：

三角形 ABC 中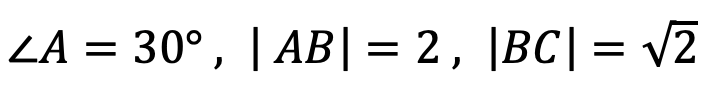，  ，求 |AC| 。

方法一：

做三角形ABC如下 

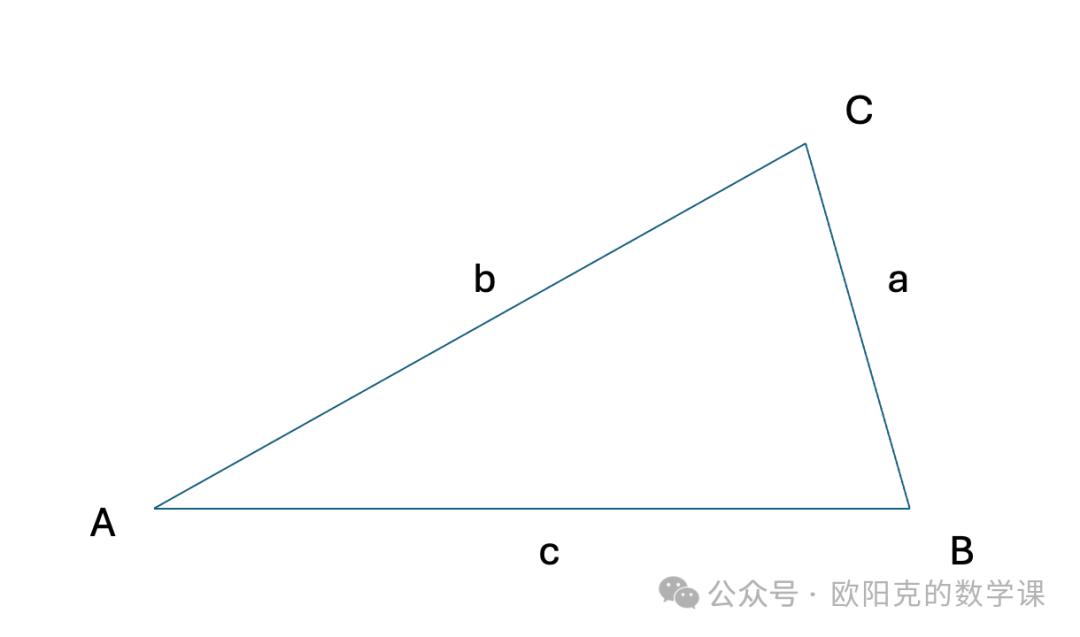
顶点A的对边边长记为 |BC| = a , 

顶点B的对边边长记为 |AC| = b , 

顶点C的对边边长记为 |AB| = c , 

根据正弦定理，

  ，

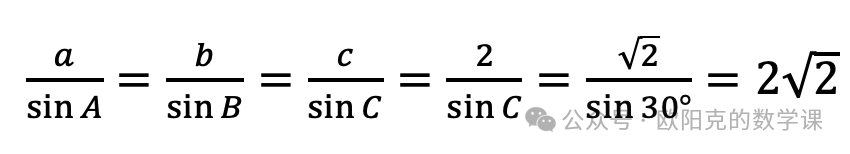则

  

 则  ，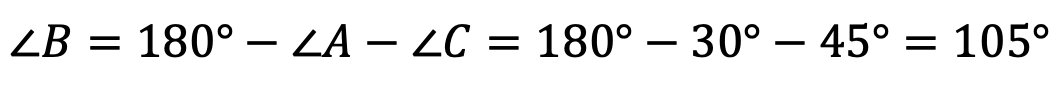

这样就求得了角B的大小，如果能求到角B的正弦值或者余弦值，就能代入到正弦定理或者余弦定理 ，从而求得AC的长度b。

这时候就需要使用三角函数的两角和公式:

 

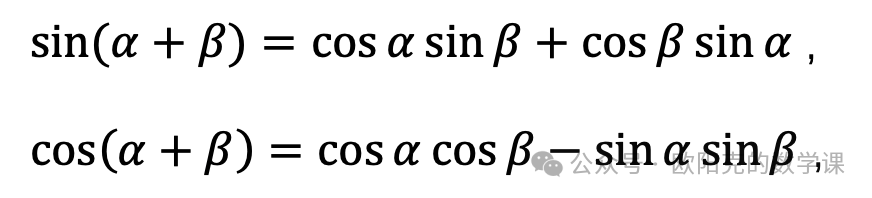
我们使用前者，

 

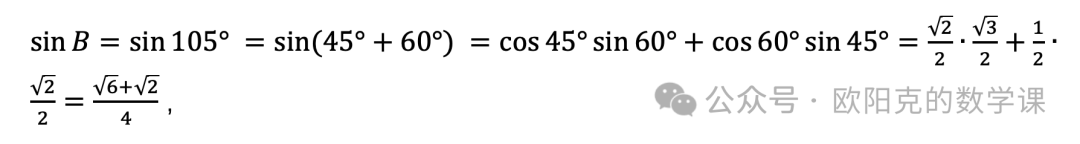
代入正弦定理可得

  ，

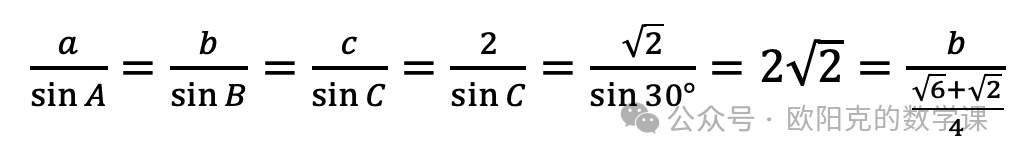解得

 。

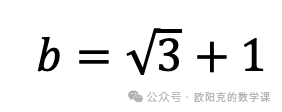这就做完了吗？

很遗憾，如果试卷上你写的是这个答案，那是不能得分的。

问题出在，钝角。

大部分同学能够牢牢记得，等腰直角三角形的的两个底角的正弦值和余弦值都是   ，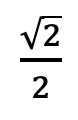

所以  ，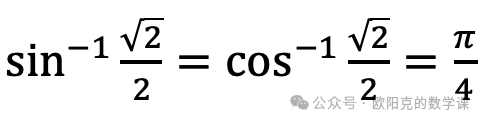

这没问题，但是，

为了使反三角函数成为函数（单值函数），反正弦的定义域是被限制在 [-1, 1] 的，值域被限制在  ，反余弦的值域则限制在 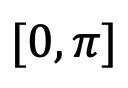 ，如下图，绿色为反正弦函数，蓝色为反余弦函数。

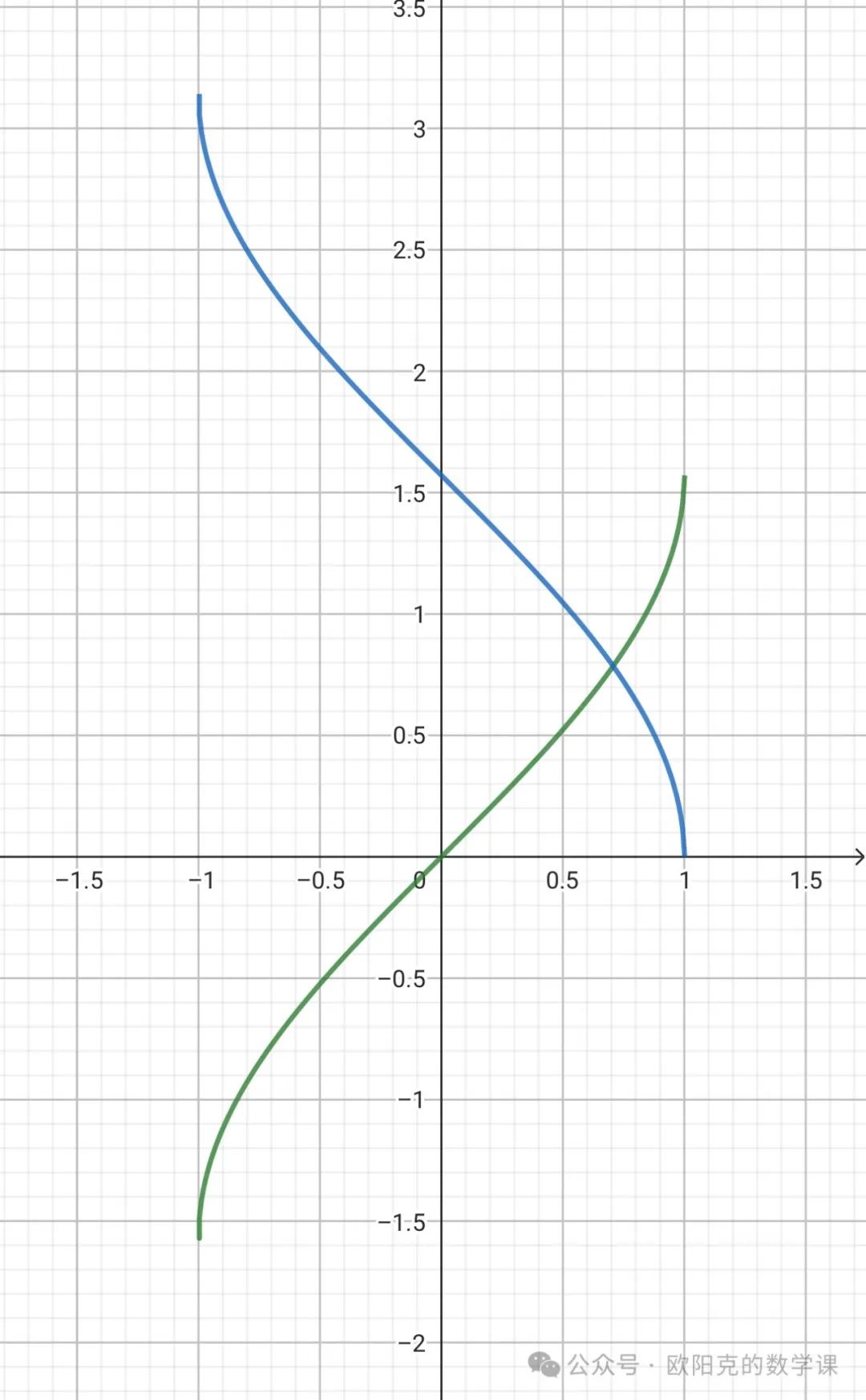
而根据正弦函数的图像，

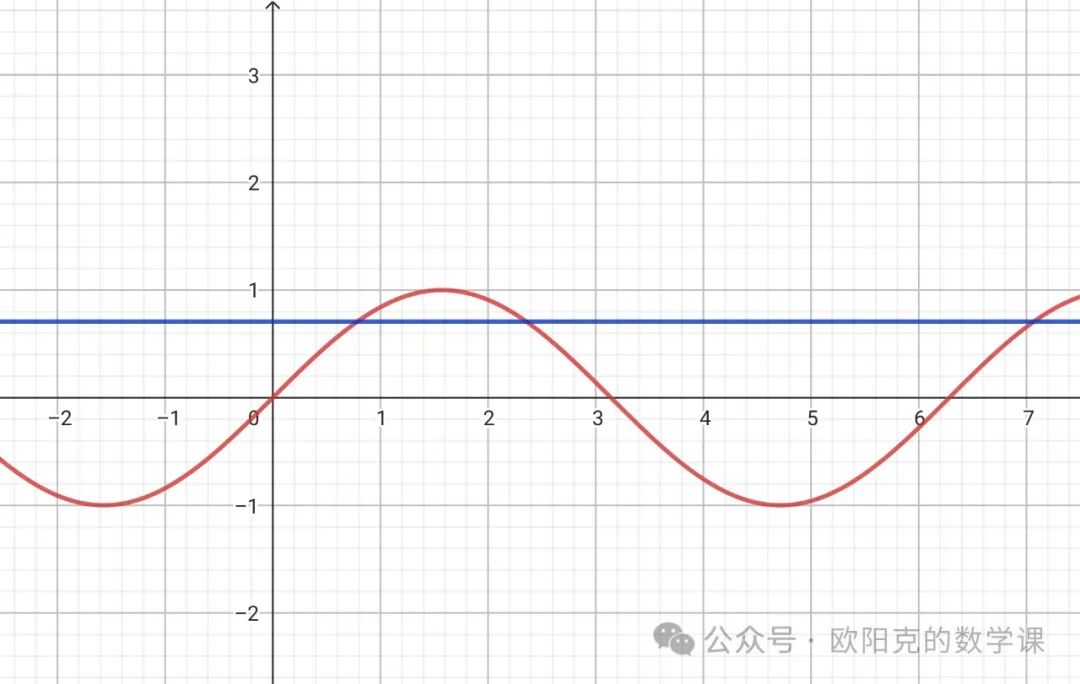
在任意三角形内角的可能取值范围内（即0至  ），每一个y值都对应着两个x值 x₁ 和 x₂（直角时 x₁ = x₂），

由图中可以看出，因为正弦函数关于 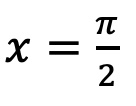  左右对称，所以在  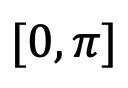上x₁ 加 x₂刚好等于  ，即

三角形内角的正弦值等于它的补角的正弦值。

推广到整个实数轴，就有了正弦函数的诱导公式（之一）

 。

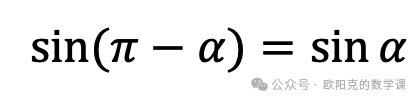回到原题，

在原图上过点B向AC作高BD，垂足为D，在AD上找到点C关于D的对称点C'，

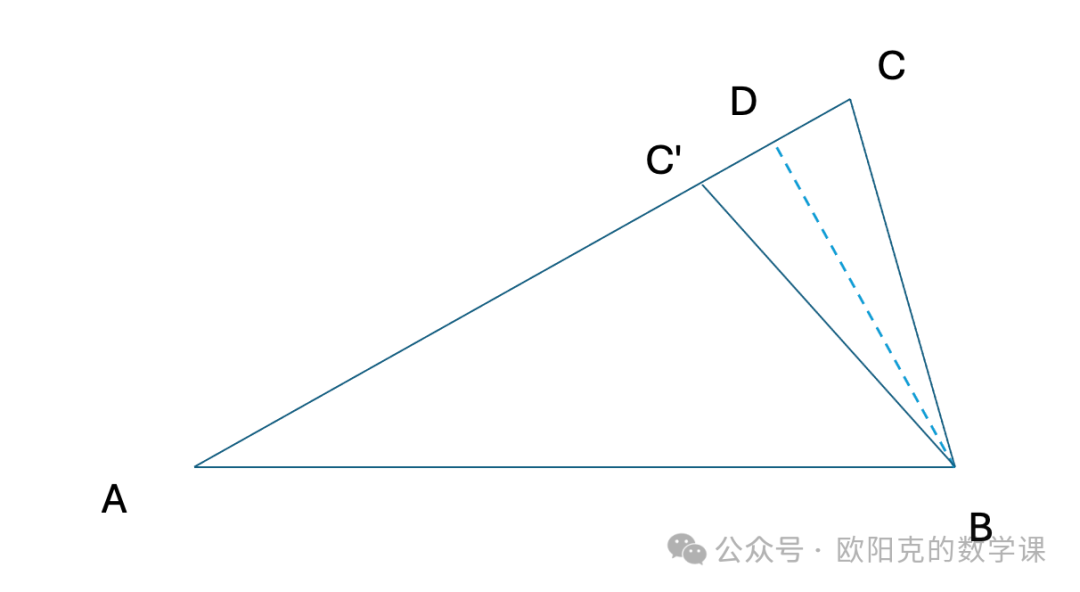
则很明显三角形 ABC' 也是符合题意（角A和边AB、BC大小固定）的三角形，且角 AC'B 和角ACB 互补。

所以我们刚才的解答漏掉了角C是钝角的情况，应该改为

  ，

则还有一种情况，就是

 ，

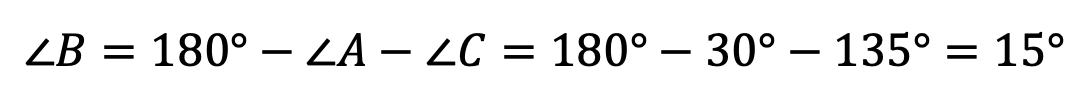这时我们需要使用三角函数的两角差公式:

 ，

则

 

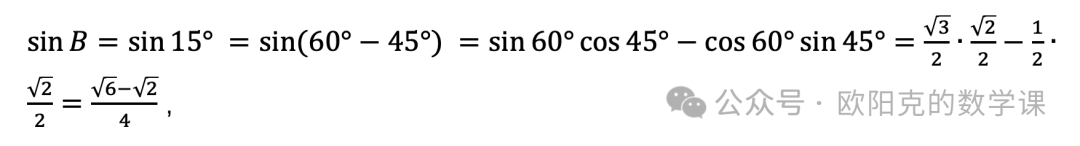
代入正弦定理可得

  ，

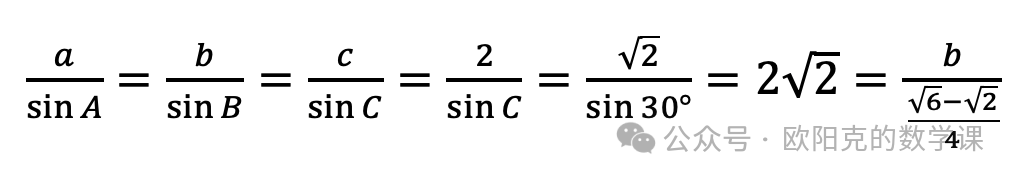解得

 。

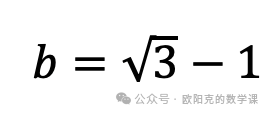所以最终答案是

 。

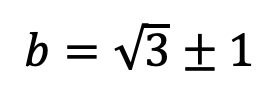如果换用余弦定理来做，那就要先求得

  ，

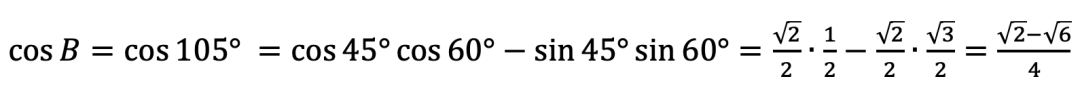或

  ，

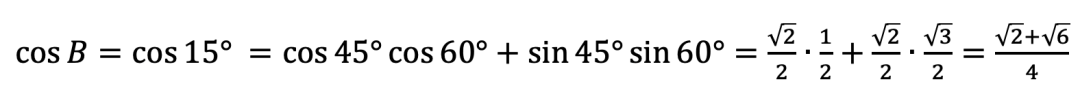代入余弦定理得

 ，

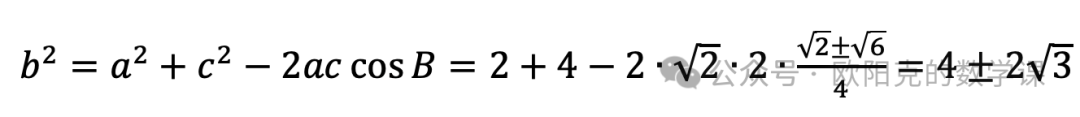则

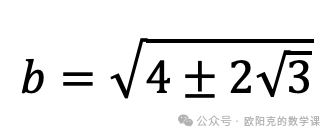  ，（边长为正数）。

等一下，这怎么和正弦定理做出的结果不一样啊？

不要慌，稍作验证可知，

 ，

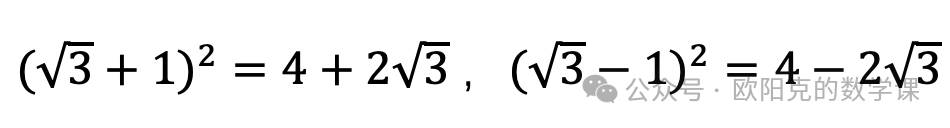请保持对完全平方的敏感。

方法二：

由方法一我们可以体会到，做三角形的题目时，千万要注意三角函数的周期性和对称性，或者说作图时千万别忘了钝角三角形，否则就可能会有所遗漏。

那么有什么方法可以避免遗漏吗？

一般来说，可以考虑使用纯代数方法来避免遗漏。

这就有了方法二。

对任意三角形，其面积都等于两夹边之积乘夹角正弦值的一半，即

  。

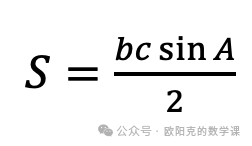又等于半周长与各边长之差依次（轮流）相乘，再乘以半周长，最后开方，即海伦公式

 。

则代入本题， 

 ，

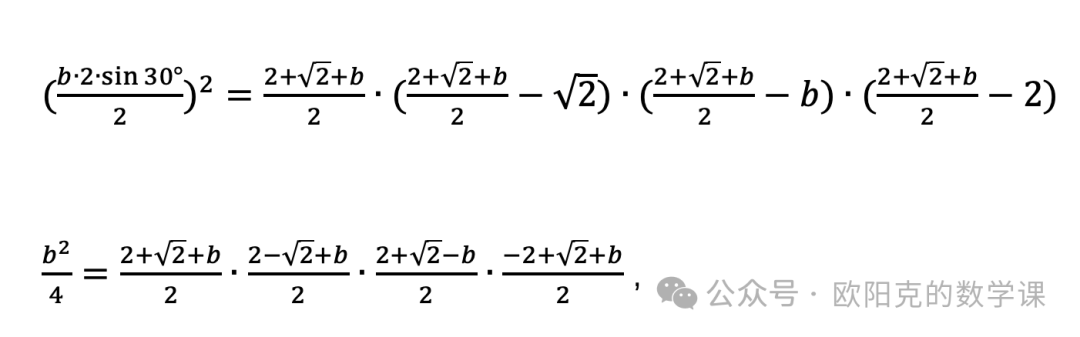反复使用平方差公式可以快速化简，

 ，

因为边长为正数，所以

 ，

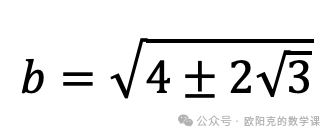再根据三角形成立的条件进行验证，即

两边之和大于第三边，两边之差小于第三边，

 ，

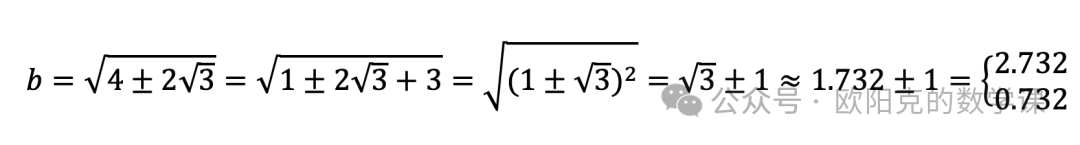可知 a+b>c，a+c>b，b+c>a，|a-b|

两个三角形都存在，因此两个解都是答案，

可见纯代数方法不需要考虑钝角三角形，只需要解方程，然后验证方程的根是否符合题意即可。

则答案就是 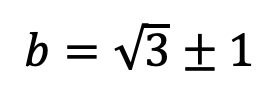 ，也可写成  。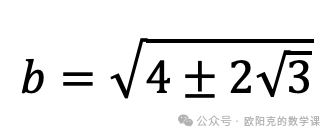

不难看出，使用方法一中的正弦定理加两角和（差）公式是最快捷的。

但是，三角函数的两角和（差）公式

 

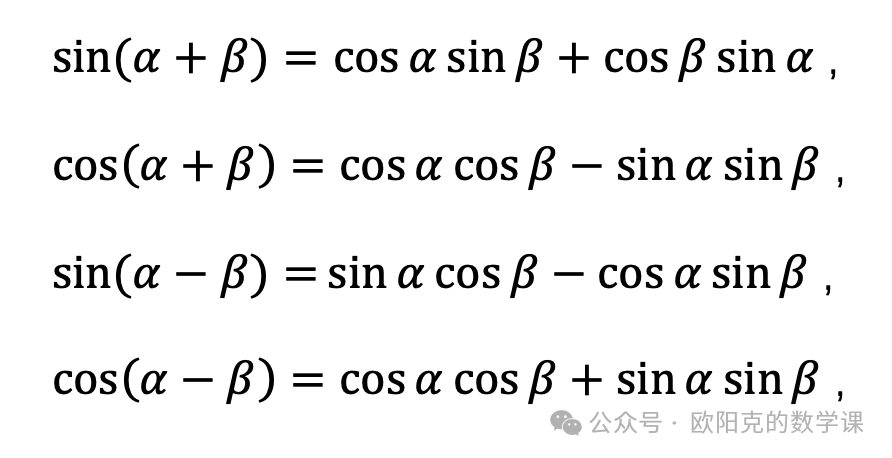
并不容易记忆，还很容易混淆。

要命的是，三角函数相关的公式需要记忆的非常之多，包括但不限于：

倍角公式

三倍角公式

半角公式

两角和公式

两角差公式

积化和差公式

和差化积公式

降幂公式

...

等等。

课本上的各种几何证明固然巧妙，但是使用和记忆仍然很是麻烦。

三角函数岂是如此不便之物？