2020年起，6年级设决赛环节。

第一部分：试题

一、填空题（满分80分，每小题8分）

1、若三个质数x、y、z，使得等式xyz+7=2020成立，则x+y+z=？

2、如图所示，由O点引出的6条射线形成的角满足∠AOB=∠BOC=∠COD=

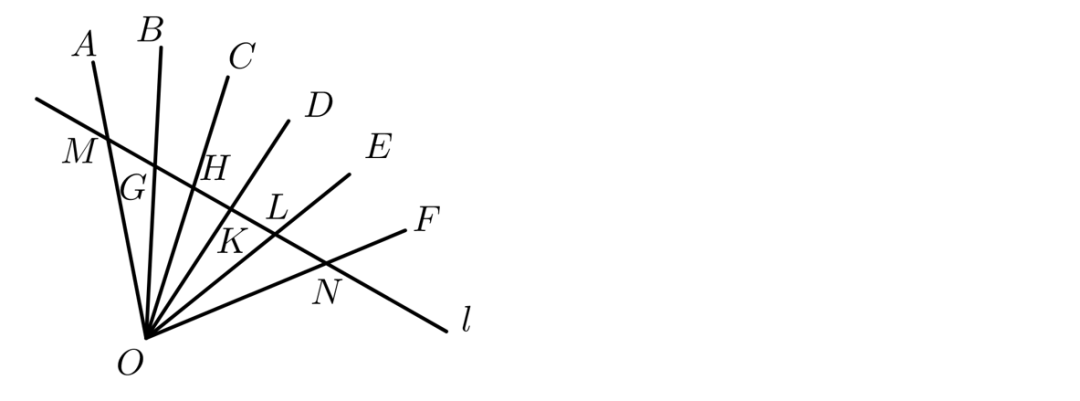
∠DOE=∠EOF=18°。直线L分别交这6条射线依次于点M、G、H、K、L、N，则图中至少有锐角多少个？

3、四个两位数的乘积“众志×成城×防控×疫情”中，相同的汉字表示相同的数字，不同的汉字表示不同的数字，这个乘积数值的结尾最多可连续有多少个零？

4、边长分别为8cm和6cm的两个正方形ABCE与BEFG如图并排放在一起，连接AF交BD于P，则四边形BPFE的面积是多少平方厘米？

5、由0、1、2、3、4、5、6、7、8、9这十个数字，每个数字只用一次排出可能得十位数，将这些十位数从小到大自左向右排成一行，则从左向右的第6个数是？

6、一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，含盐百分比变为12%；第三次再加入同样多的水，盐水的含盐百分比将变为多少？

7、在1-1000000的自然数中，所有7的倍数的和等于？

8、今年，祖父的年龄是小学生明明年龄的6倍，几年过去了，祖父的年龄将是明明年龄的5倍，又过去了几年以后，祖父的年龄是明明年龄的4倍，祖父今年多少岁？

9、如图是一个容积为30立方厘米的正方体铁皮盒被剪去的一个“角”后的平面展开图（图中相同字母表示长度相等的线段）各侧面剪掉的三个阴影三角形的面积分别是2平方厘米，3平方厘米，3平方厘米，则该铁皮盒最多可以装多少立方厘米的水？

10、在2名六年级选手与至少10名五年级选手一起进行比赛象棋，每两个人彼此都恰好比赛一场，每场比赛胜者得2分，负者得0分，若和局则各得到1分．比赛结束后，已知2名六年级的选手得分之和是20分，且每名五年级选手都得到了N分，则N=?

二、解答题（满分70分，11题10分，12-15题各15分）

11、(50/9-0.8+22/9)×(7.6÷4/5+12/5×1.25)

12、一个六位数abcdef满足defabc=6×abcdef，试确定这个六位数abcdef的值，并且写出求解过程。

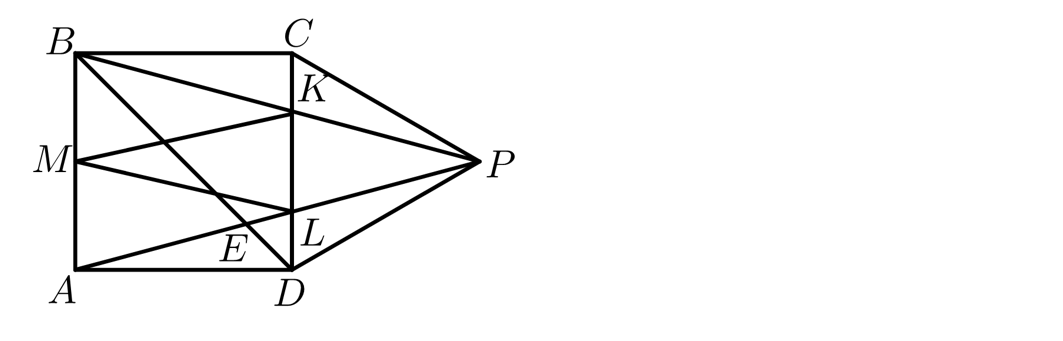
13、如图所示，ABCD是正方形，PCD是面积为1的正三角形，线段AP交BD、CD分别于E和L，BP交CD于点K，取AB中点M，连接MK、ML。

(1) 证明：BE=PE

(2) 求四边形PKML的面积

14、如果一个三角形的三条边长是彼此不等的三个质数，这样的三角形叫做“鹏程三角形”。

(1) 试举一个鹏程三角形的实例。

(2) 证明：不存在周长为2020的鹏程三角形。

(3) 证明：鹏程三角形一定不是直角三角形。

15、在一个平地上站着n个人，对每个人来说，他到其他的人的距离均不相同，当有火灾信号发出的时候，每人都用水枪击中距离他最近的人。

(1) 当n=2020时，请你举例说明，可能每个人都是湿的。

(2) 当n=2021时，证明至少有一个人身上是干的。

第二部分：解析

一、填空题（满分80分，每小题8分）

1、若三个质数x、y、z，使得等式xyz+7=2020成立，则x+y+z=？

由题意知xyz=2013，将2013分解质因式=3×11×61。所以x+y+z=3+11+61=75。

2、如图所示，由O点引出的6条射线形成的角满足∠AOB=∠BOC=∠COD=

∠DOE=∠EOF=18°。直线L分别交这6条射线依次于点M、G、H、K、L、N，则图中至少有锐角多少个？

以O为顶点的角中，18°有5个，36°有4个，54°有3个，72°有2个。另L与各边相交，形成6组24个角，其中最多有一组是4个直角，其它每对有2个锐角和2个钝角，共10个锐角。图中至少有锐角5+4+3+2+10=24个。

3、四个两位数的乘积“众志×成城×防控×疫情”中，相同的汉字表示相同的数字，不同的汉字表示不同的数字，这个乘积数值的结尾最多可连续有多少个零？

末尾0的数量取决于乘积中5和2的因数数量，相较而言，2比较容易构建，但5最多仅能构建出3个，即25或75+任一个整10数，所以，结尾最多可连续有3个零。

4、边长分别为8cm和6cm的两个正方形ABCE与BEFG如图并排放在一起，连接AF交BD于P，则四边形BPFE的面积是多少平方厘米？

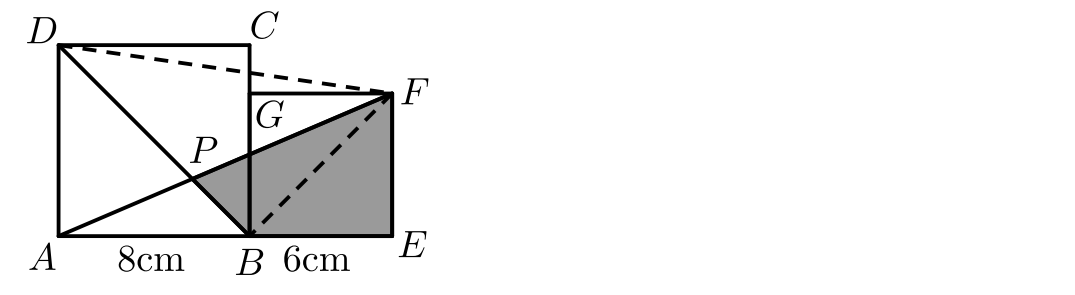
连接DF、BF，S△ABF=1/2×8×6=24cm²；S△ADF=1/2×8×14=56cm²；可知DP/BP=S△ADF/S△ABF=7/3。因S△ABD=1/2×8×8=32cm²，S△ABP=3/10×32=9.6cm²。而S△AEF=1/2×6×14=42cm²。S四边形BPFE=42-9.6=32.4cm²。

5、由0、1、2、3、4、5、6、7、8、9这十个数字，每个数字只用一次排出可能得十位数，将这些十位数从小到大自左向右排成一行，则从左向右的第6个数是？

这些数从小到大为1023456789,1023456798,1023456879,1023456897,

1023456978,1023456987。第6个数是1023456987。

6、一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，含盐百分比变为12%；第三次再加入同样多的水，盐水的含盐百分比将变为多少？

设第一次加水后，盐水共有100份，盐有15份，15÷12%=125份，第二次加入的水为25份，第三次再加入25份水，含盐百分比=15÷（100+25+25）=10%。

7、在1-1000000的自然数中，所有7的倍数的和等于？

1000000÷7=142857余1，即所有7的倍数的和=7×（1+142857）×142857÷2=7×142857×(142858÷2)=999999×71429=(1000000-1)×71429=71428928571。

8、今年，祖父的年龄是小学生明明年龄的6倍，几年过去了，祖父的年龄将是明明年龄的5倍，又过去了几年以后，祖父的年龄是明明年龄的4倍，祖父今年多少岁？

有题意可知，祖父和明明的年龄差是5、4、3的倍数，[5、4、3]=60，年龄差为60岁，从今年来看，60等于5份明明的年龄，明明今年12岁，祖父今年72岁。

9、如图是一个容积为30立方厘米的正方体铁皮盒被剪去的一个“角”后的平面展开图（图中相同字母表示长度相等的线段）各侧面剪掉的三个阴影三角形的面积分别是2平方厘米，3平方厘米，3平方厘米，则该铁皮盒最多可以装多少立方厘米的水？

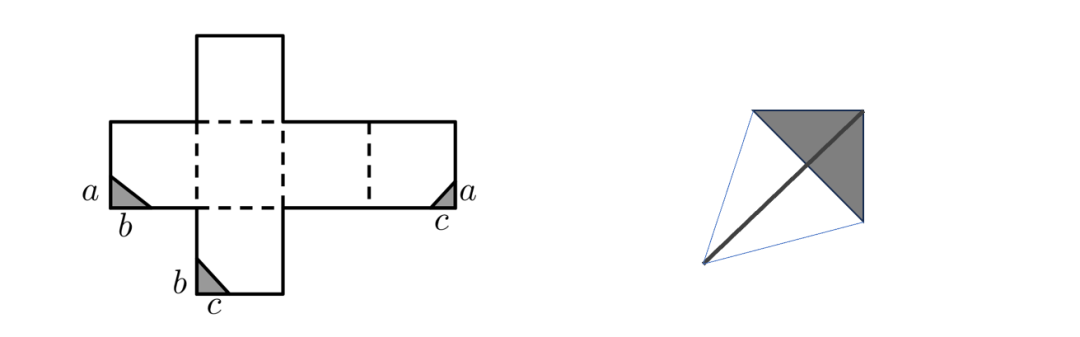由题中信息可以求出a、b、c分别为2、2、3厘米。剪掉的三角形在正方体的一个角汇聚，形成右侧四面体。铁皮盒最多可以装的水，即用铁皮盒体积减去小四面体体积。小四面体体积=1/2×(2×2)×3×1/3=2立方厘米，铁皮盒最多可以装28立方厘米的水。

10、在2名六年级选手与至少10名五年级选手一起进行比赛象棋，每两个人彼此都恰好比赛一场，每场比赛胜者得2分，负者得0分，若和局则各得到1分．比赛结束后，已知2名六年级的选手得分之和是20分，且每名五年级选手都得到了N分，则N=?

设5年级有n人，则所有选手总得分=(n+2)(n+1)，N=[(n+2)(n+1)-20]/n=(n²+3n-18)/n=n+3-18/n，因n≥10，要使N为整数，n=18。N=20分。

二、解答题（满分70分，11题10分，12-15题各15分）

11、(50/9-0.8+22/9)×(7.6÷4/5+12/5×1.25)

答案=90。

12、一个六位数abcdef满足defabc=6×abcdef，试确定这个六位数abcdef的值，并且写出求解过程。

根据位值原理1000def+abc=6000abc+6def，994def=5999abc，142def=857abc，因142和857互质，所以def=857，abc=142。abcdef=142857。

另，如对n/7熟悉，可知原式=1/7×6=6/7，即0.142857×6=0.857142，可得到结果。

13、如图所示，ABCD是正方形，PCD是面积为1的正三角形，线段AP交BD、CD分别于E和L，BP交CD于点K，取AB中点M，连接MK、ML。

(1) 证明：BE=PE

(2) 求四边形PKML的面积

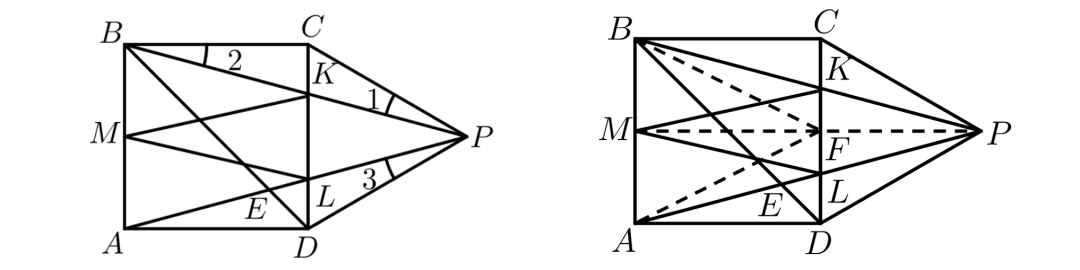
(1)见左图，因为BC=CP，且△PCD是正三角形，所以∠1=∠2=（180°-90°-60°）÷2=15°；同理，∠3=15°。可知∠EBP=90°-45°-15°=30°；而∠BPE=60°-15°-15°=30°，△BEP是等腰三角形，BE=PE。

(2)见右图，连接BF、AF、MF、PF。因为△CPF和△BPF同底等高，面积相同，所以S△CPK=S△BKF，而S△BKF=S△MKF，所以S△MKF=S△CPK，同理可证S△MLF=S△LPD，S四边形PKML=S△CPD=1。

14、如果一个三角形的三条边长是彼此不等的三个质数，这样的三角形叫做“鹏程三角形”。

(1) 试举一个鹏程三角形的实例。

(2) 证明：不存在周长为2020的鹏程三角形。

(3) 证明：鹏程三角形一定不是直角三角形。

(1)如：3、5、7。

(2)不存在。三个质数相加和为偶数，其中必有2，而任意2个质数之间相差2，所以2与另外2个质数无法构成三角形。

(3)假设三角形三边为a、b、c，要使其为直角三角形，即a²+b²=c²，根据奇偶性判断，a、b、c中必有一个偶数，即2，而根据（2）可知，不存在边长为2的三角形，所以鹏程三角形一定不是直角三角形。

15、在一个平地上站着n个人，对每个人来说，他到其他的人的距离均不相同，当有火灾信号发出的时候，每人都用水枪击中距离他最近的人。

(1) 当n=2020时，请你举例说明，可能每个人都是湿的。

(2) 当n=2021时，证明至少有一个人身上是干的。

(1)把2020个人每2人分成一个组，可令每组两人间的距离互不相同，但小于他们与其他人的距离，这样同组的人会相互攻击，所有人都是湿的。

(2)先考虑距离最短的2人，他们会相互击中，再考虑剩下的2019个人中距离最近的2人，这2人要不就是攻击对方，要不就是攻击之前的2人；接着，依次考虑剩下的人中距离最近的2人，这2人同上，要不攻击对方，要不攻击之前的人。最终，至少有1人是干的。