2020年起，鹏程杯考卷分数从120分调整到150分。

第一部分：试题

一、填空题（满分80分，每小题8分）

1、两个质数与1之和等于2020，则这两个质数的积等于？

2、一棵参天大树，树干周长为3米。地上有一根常青藤恰好绕了它5圈，藤尖 离地面20米高。那么，这根常青藤至少有多少米？

3、若正整数n使得3n-4, 4n-5和5n-3都是质数，则这三个质数的乘积等于多少？

4、被2、3、4、5、6除都余1且被7整除的自然数中最小的一个是多少？

5、如图，在一个大正方形纸片中，剪掉两个带阴影的正方形：一个为甲，另一个为乙。已知甲的面积是16cm²，则乙的面积是多少？

6、甲、乙汽车分别从A、B两站同时出发相向而行，两车第一次在距A站32千 米的C处相遇，相遇后两车继续行进，各自到达B、A两站后，立即沿原路返回，第二次在距A站64千米的D处相遇。则A、B两站的距离是多少千米？

7、一队少年儿童不超过50人，围成一圈做游戏。每个儿童的左、右相邻的都恰是一个男孩和一个女孩。则这队少年儿童最多有多少人？

8、一个长方体，长:宽=2:1，宽:高=3:2。如果长方体所有棱长之和是220厘米，则长方体的体积是多少立方厘米？

9、战斗在抗击“新冠肺炎”第一线的钟南山院士出生的公元年份数是个完全平方数，那么今年（2020年）钟院士已经是多少岁？

10、由一条公路对A、B、C、D四个居民点依次开通四条道路（如图）。已知沿道路一公路—道路由A到B的路程等于9千米，由A到C的路程等于13千米， 由B到C的路程等于8千米，而由B到D的路程等于14千米。则由A到D的路程等于多少千米？

二、解答题（满分70分，11题10分，12-15题各15分）

11、计算：0.4×[11/52÷11/4×(4.3-1.8)] ×26

12、

(1)试将505写成10个连续自然数之和；

(2)能将2020写成10个连续自然数之和吗？如果能，把它写出来；如果不能，说明理由。

13、小明在一张平面曲边薄板的边缘上选取5个点A、P、B、C、D，如图所示。已知AB//DC且AB = DC。连接PD交AB于E，连接PC交AB于F，连接EC。已知△PAE 的面积=1.5, △PBF的面积=2.5，求△CEF的面积。

14、对于任意的n个自然数，总能选出其中的4个数a、b、c、d，使得(a—b)(c-d) 被2020整除。试确定n的最小值，简述你的理由。

15、现在有100个人参加象棋单循环赛，每两人都对弈一局且决出胜负。

(1)求总共对弈多少局？

(2)证明：比赛结束后，一定可以将这100个人列为一队，使得队列中的每一个

人都战胜了紧跟在他后面的那个人！

第二部分：解析

一、填空题（满分80分，每小题8分）

1、两个质数与1之和等于2020，则这两个质数的积等于？

两个质数和为2019，只能是2和2017，积为4034。

2、一棵参天大树，树干周长为3米。地上有一根常青藤恰好绕了它5圈，藤尖 离地面20米高。那么，这根常青藤至少有多少米？

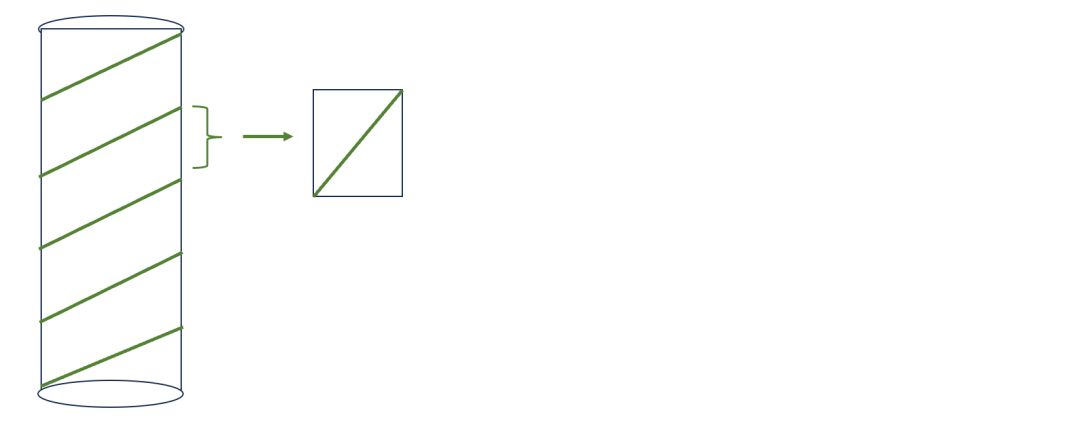
每段常青藤与树干周长（3米）、树干高度（20/5=4米）构成直角三角形。常青藤长度=5×5=25米。

3、若正整数n使得3n-4, 4n-5和5n-3都是质数，则这三个质数的乘积等于多少？

对任意正整数n，4n-5总是奇数，而3n-4和5n-3则奇偶性相反。其中必有一个为2。

若3n-4=2，则n=2。此时4n-5=3，5n-3=7，符合题意。

若5n-3=2，则n=1。此时4n-5=-1，不符合题意。

这三个质数乘积=2×3×7=42。

4、被2、3、4、5、6除都余1且被7整除的自然数中最小的一个是多少？

所求的数减1，是2、3、4、5、6的倍数。2、3、4、5、6的最小公倍数是60，所以61、121、181、241、301、361……都是被2、3、4、5、6除余1的数，其中能被7整除的最小一个数是301。

5、如图，在一个大正方形纸片中，剪掉两个带阴影的正方形：一个为甲，另一个为乙。已知甲的面积是16cm²，则乙的面积是多少？

设大正方形面积为2a，两个等腰直角三角形的面积为a，从图中可知，甲的面积是4/9a，求得a=36cm²，乙的面积等于1/2a=18cm²。

6、甲、乙汽车分别从A、B两站同时出发相向而行，两车第一次在距A站32千 米的C处相遇，相遇后两车继续行进，各自到达B、A两站后，立即沿原路返回，第二次在距A站64千米的D处相遇。则A、B两站的距离是多少千米？

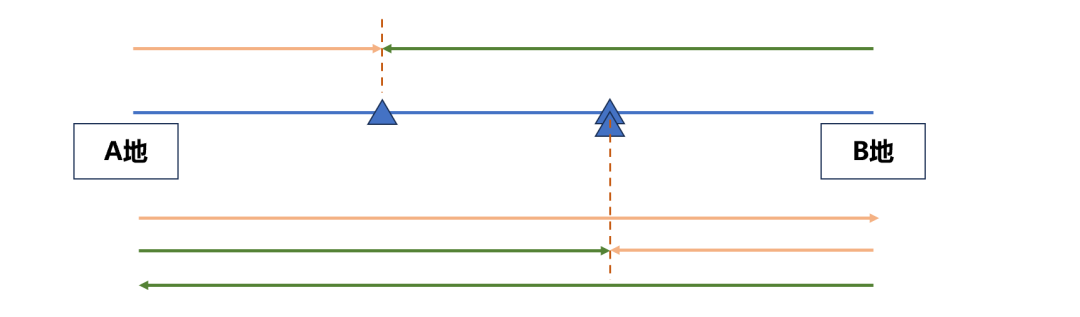如图，设AB两地距离为x，32/(x-32）=（2x-64）/(x+64），解得x=80千米。

7、一队少年儿童不超过50人，围成一圈做游戏。每个儿童的左、右相邻的都恰是一个男孩和一个女孩。则这队少年儿童最多有多少人？

设n个少年儿童围成一圈，每个儿童的左、右相邻的都恰是一个男孩子和一个女孩，那么，一定是两个男孩和两个女孩依次相邻：…男男女女男男女女…要使其首位相连，n必须是4的倍数，最多可有48人。

8、一个长方体，长:宽=2:1，宽:高=3:2。如果长方体所有棱长之和是220厘米，则长方体的体积是多少立方厘米？

220÷4=55，即三条棱长和为55，因长:宽=2:1，宽:高=3:2，即长：宽：高=6:3:2，长为30厘米，宽为15厘米，高为10厘米，长方体体积=4500立方厘米。

9、战斗在抗击“新冠肺炎”第一线的钟南山院士出生的公元年份数是个完全平方数，那么今年（2020年）钟院士已经是多少岁？

易知45²= 2025，所以在2020前面最近的完全平方数是44²=1936。因此今年钟院士已经是2020-1936=84岁。

10、由一条公路对A、B、C、D四个居民点依次开通四条道路（如图）。已知沿道路一公路—道路由A到B的路程等于9千米，由A到C的路程等于13千米， 由B到C的路程等于8千米，而由B到D的路程等于14千米。则由A到D的路程等于多少千米？

由A到B，再由B到C，比A直接到C多出2个b端的路程，即2b=9+8-13=4，b=2。A到D的路程=A到B的路程+B到D的路程-4=9+14-4=19千米。

二、解答题（满分70分，11题10分，12-15题各15分）

11、计算：0.4×[11/52÷11/4×(4.3-1.8)] ×26

答案=2。

12、

(1)试将505写成10个连续自然数之和；

(2)能将2020写成10个连续自然数之和吗？如果能，把它写出来；如果不能，说明理由。

(1)设存在自然数 a满足 a + (a + l) + (a + 2) + (a + 3) + (a + 4) + (a + 5) + (a + 6) + (a + 7) + (a + 8) + (a + 9) = 505。即 10a + 45 = 505, 解得 a = 46。505可以写成46-55这连续10个自然数之和。

(2)同上，设存在自然数 a满足 a + (a + l) + (a + 2) + (a + 3) + (a + 4) + (a + 5) + (a + 6) + (a + 7) + (a + 8) + (a + 9) = 2020。即 10a + 45 = 2020, a无自然数解。所以，2020不能写成10个连续自然数之和。

事实上，更简便的证明方法是：10个连续自然数必有5奇5偶，和必为偶数，可证2020不能写成10个连续自然数之和。

13、小明在一张平面曲边薄板的边缘上选取5个点A、P、B、C、D，如图所示。已知AB//DC且AB = DC。连接PD交AB于E，连接PC交AB于F，连接EC。已知△PAE 的面积=1.5, △PBF的面积=2.5，求△CEF的面积。

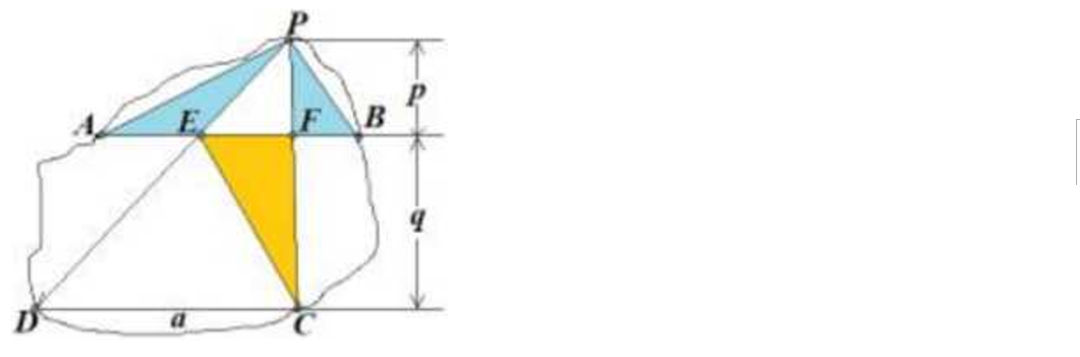
设AB=DC=a，P到AB的距离为p，到DC的距离为q。S△PDC=1/2×a（p+q），S△PAB=1/2×ap，S△DCE=1/2×aq，可知S△PDC=S△PAB+S△DCE，即S△PAB=S△PEC，即S△CEF=S△PAE+S△PBF=1.5+2.5=4。

14、对于任意的n个自然数，总能选出其中的4个数a、b、c、d，使得(a—b)(c-d) 被2020整除。试确定n的最小值，简述你的理由。

2020=101×2×2×5。要使n最小，需要（a-b）和（c-d）中较大的那个数尽量小，在本题中选定为101和20。

要使n个自然数中，选出2个数的差是101的倍数，那么至少需要有102个数，因为对任意选取的102个数，它们除以101的余数至多存在0、1、2、3、……、99、100这101种可能，根据抽屉原理，必然有2数除以101的余数相同，差为101。

同样可证，这102个数中，减去2个数后，还有100个数，其中必然有2个数除以20同余，可以找出另两个数差为20，命题得证。

15、现在有100个人参加象棋单循环赛，每两人都对弈一局且决出胜负。

(1)求总共对弈多少局？

(2)证明：比赛结束后，一定可以将这100个人列为一队，使得队列中的每一个

人都战胜了紧跟在他后面的那个人！

(1)100人，每人下99局，共对弈100×99÷2=4950局。

(2)可以让这100名选手依次上台排队。先让2人上台，胜者排在前（设为A1），负者排在后（设为A2）；第3人上台，如果他胜A1，则排A1前面，如果他负于A1再与A2比较，胜A2则排在A2前面（即A1和A2之间），若负于A2，则排在A2的后面。此后选手依次上台，从前往后逐一比较，即可站成题目所设队列。