[题目](2022年2月，北京八中高三下学期开学考，19)已知函数

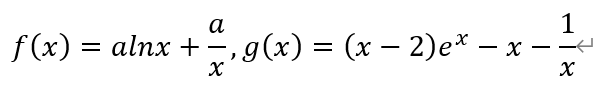
其中a≠0。

（1）求f(x)的单调区间；

（2）设当a=1时，若对任意x∈(0,1]，不等式f(x)+g(x)＜m恒成立，求整数m的最小值。

 

[解析] 1）函数f(x)的定义域为x＞0。

对函数f(x)求导，得

令f′(x)=0，解得x=1。

当a＜0时，函数f(x)在(0,1)上单调递增，在(1,+∞)上单调递减；当a＞0时，函数f(x)在(0,1)上单调递减，在(1,+∞)上单调递增。

 

2）当a=1时，有

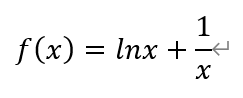
根据已知，当x∈(0,1]，满足

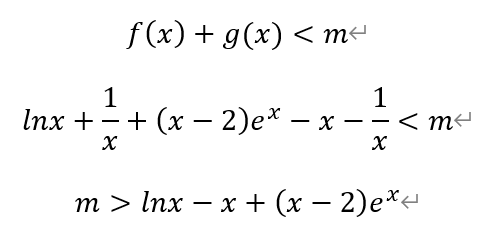
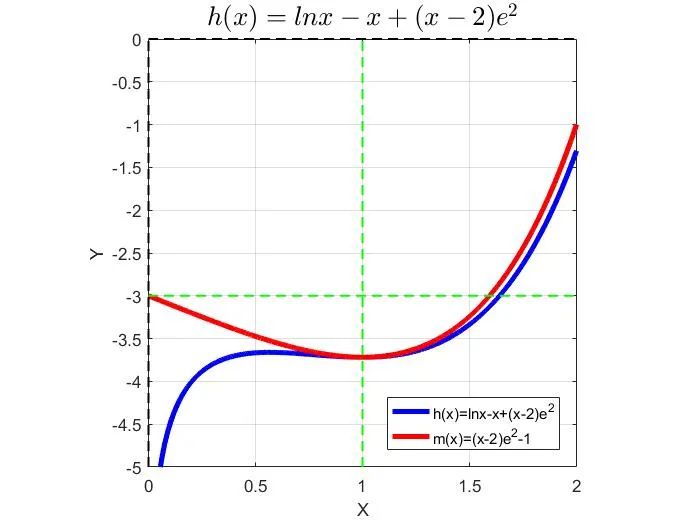
构造函数h(x)

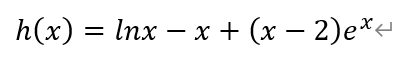
其中x∈(0,1]。

欲求m的最小整数值，需要先求m的最小值，等价于求函数h(x)的最大值。

 

方法一：

对函数h(x)求导，得

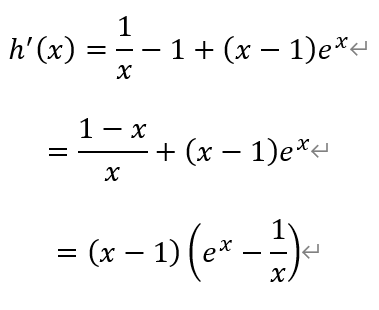
构造函数m(x)，

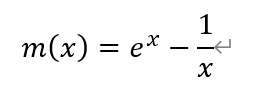
其中x∈(0,1]。

由于x＜1，所以h′(x)的符号与函数m(x)的符号相反。

对函数m(x)求导，有

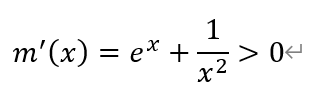
即函数m(x)在定义域上单调递增。

又由于

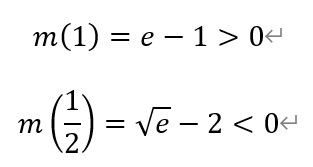
根据零点存在定理，函数m(x)在(1/2,1)上存在唯一零点x0，使得

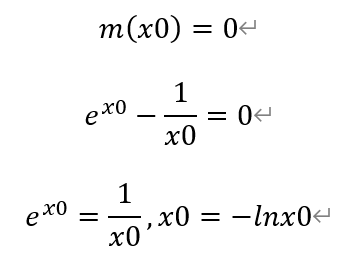
当x变化时，h(x)和h＇(x)变化情况如下

x	(0,x0)	x0	(x0,1)
h＇(x)	＋	0	－
h(x)	↗	极大	↘

函数h(x)在x0处取得最大值，即

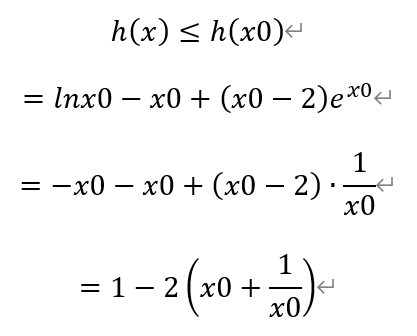
由于函数n(x),

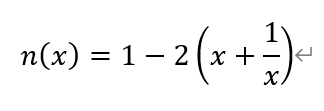
在(0,1]上单调递增，所以

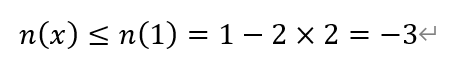
从而m的最小整数值为-3。

 

方法二：利用切线放缩公式，

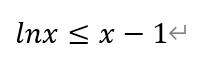
当且仅当x=1时取等号。

对函数h(x)进行放缩，有

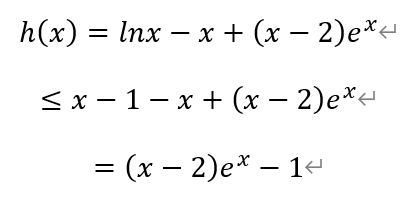
构造函数t(x)，

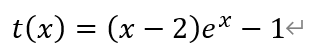
其中x∈(0,1]。

欲求函数h(x)的最大值，等价于求函数t(x)的最大值。

对函数t(x)求导，得

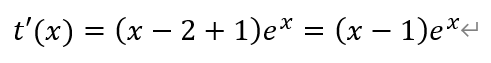
令t′(x)=0，解得x=1。由于x∈(0,1]，所以t′(x)＜0，即函数t(x)单调递减。从而有

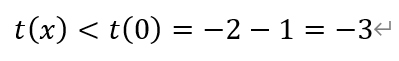
从而m的最小整数值为-3。