[题目](2022年2月，北京八中高三下学期开学考，20)已知⊙F1：(x+1)²+y²=16，F2(1,0)，M为⊙F1上的动点。若线段MF2的垂直平分线交MF1于点P。

（1）求动点P的轨迹C的方程；

（2）已知T(1,y0)(y0＞0)为C上一点，过T作斜率互为相反数且不为0的两条直线TA,TB，分别交曲线C于点A,B。求|AB|的取值范围。

 

[解析]1）连接PF2。由于PN为PF2的垂直平分线，所以MP=PF2。

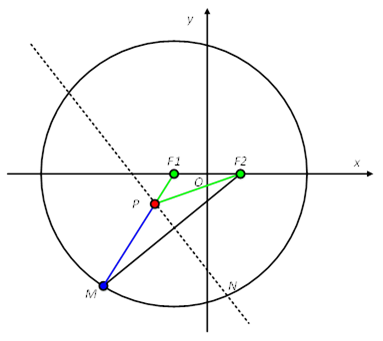
于是，有

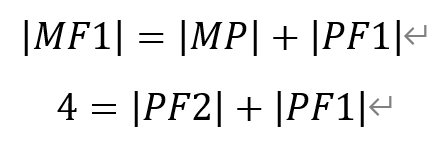
即点P为到两个定点的距离之和为定值的点的轨迹，它是一个椭圆。其中，2a=4，a=2，c=1。从而有，b²=a²-c²=4-1=3。因此，点P的轨迹方程为，

 

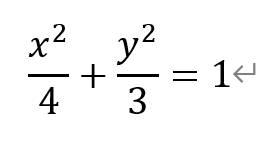
2）由于点T的横坐标为1，所以代入椭圆的方程，有

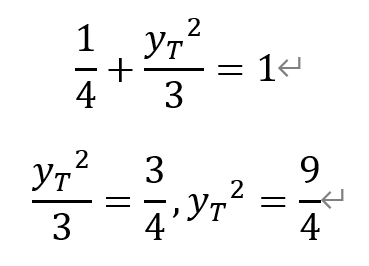
解得，y_t=±3/2。不失一般性，取正，即T(1,3/2)。

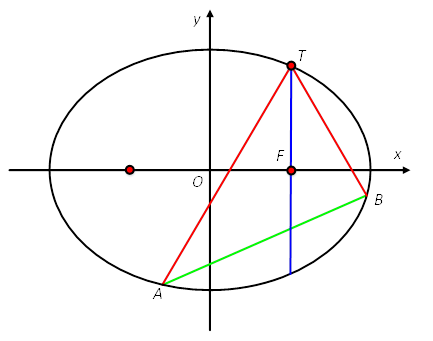
设直线AB的方程为：y=kx+m。与椭圆的方程联立有，

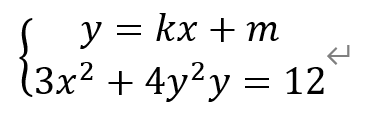
消去y，得到一个关于x的一元二次方程，

其中，

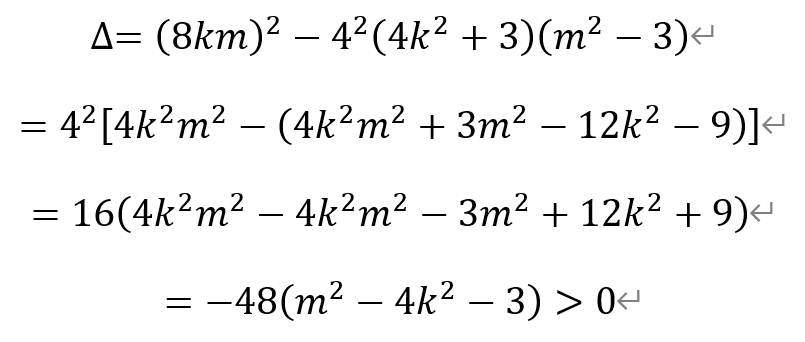
即

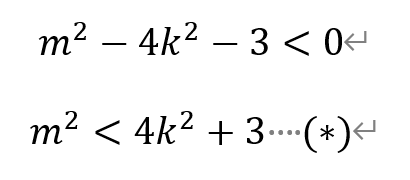
设点A(x1,y1)，B(x2,y2)。则有

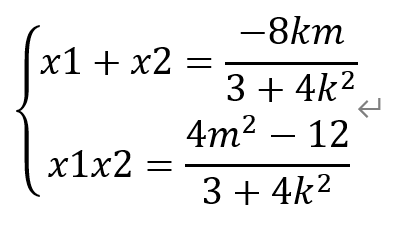
又，直线TA和TB的斜率为

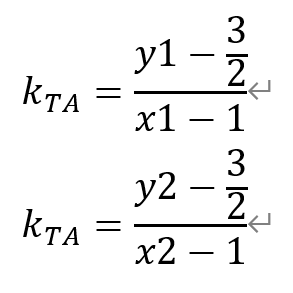
它们互为相反数，即

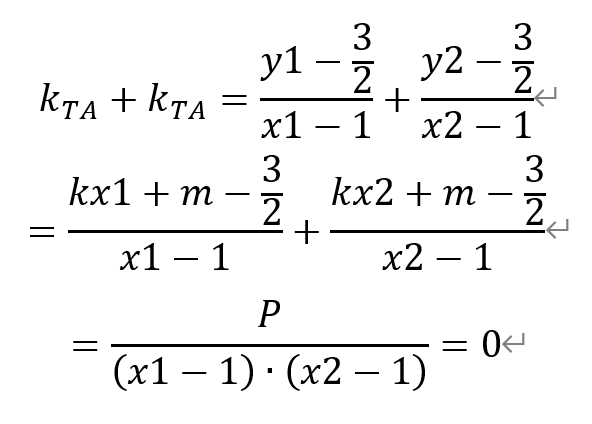
其中，

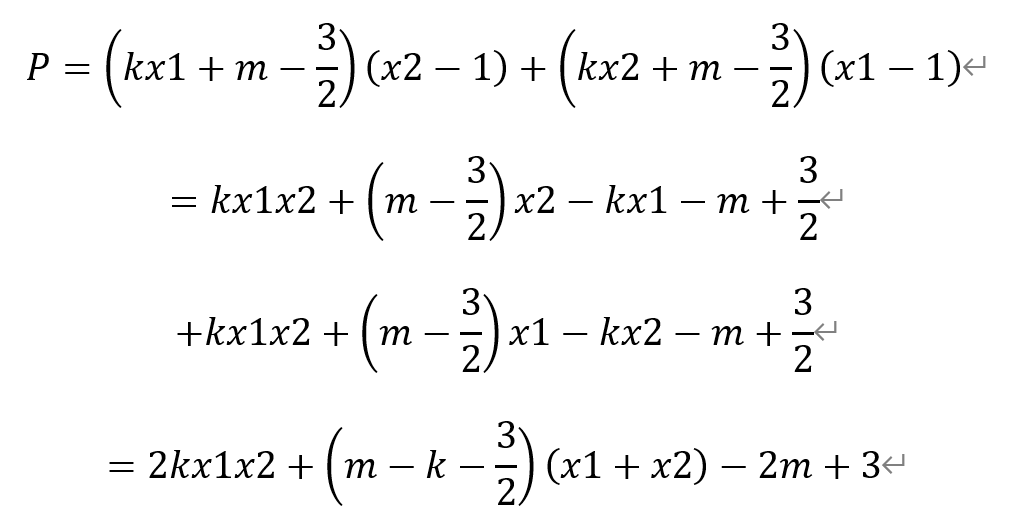
将前述x1+x2和x1x2的值代入，有

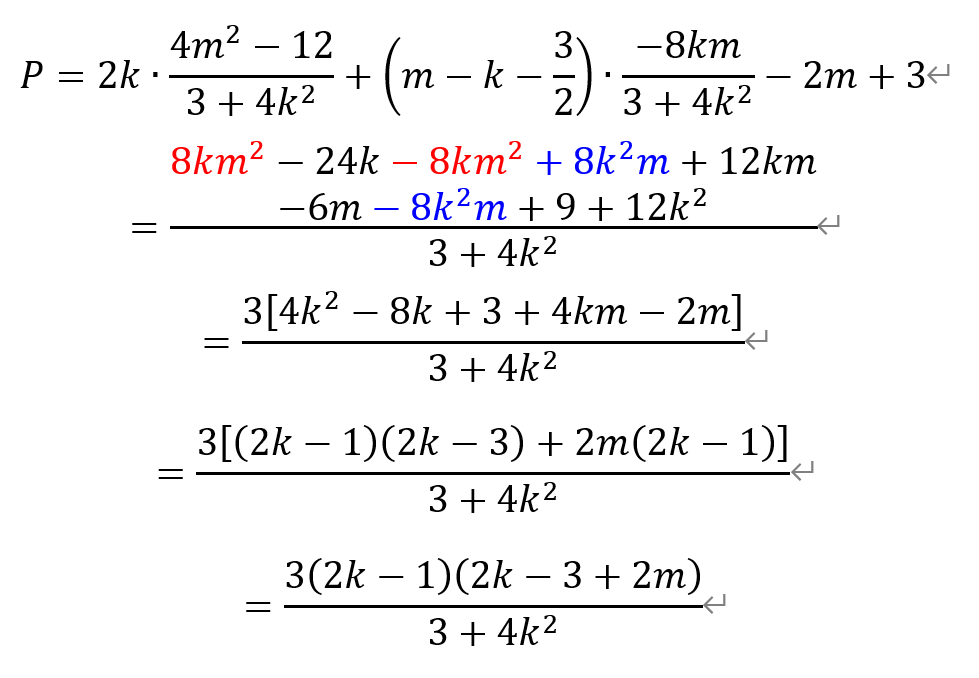
于是，有

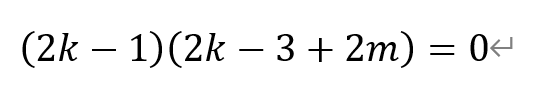
解得

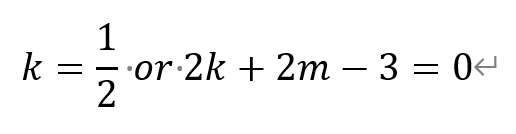
若2k+2m-3=0，则有

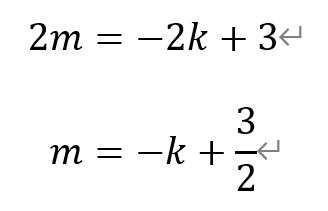
代回直线AB的方程，有

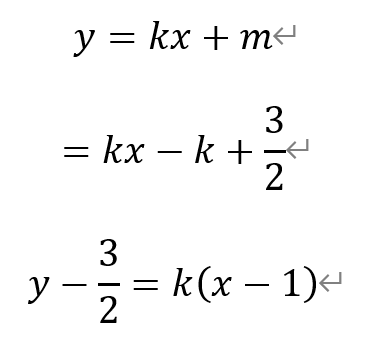
即直线AB过点T。由于直线TA和TB的斜率不为0，所以这种情况不符合题意。

从而有k=1/2。根据（*）有

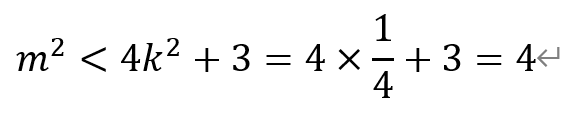
从而，线段AB的长度为

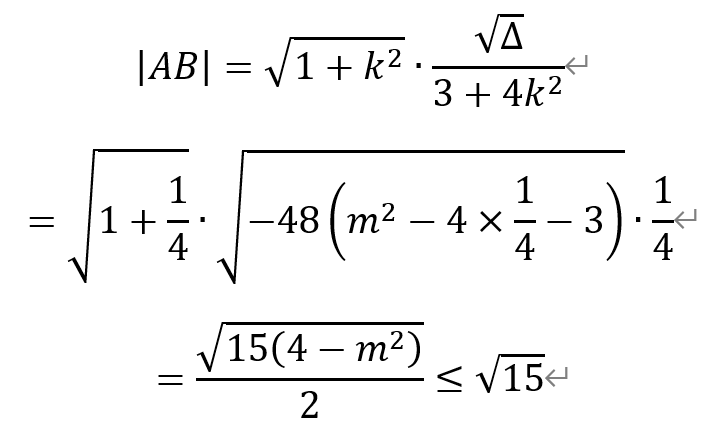
即|AB|的取值范围为(0,√15]。