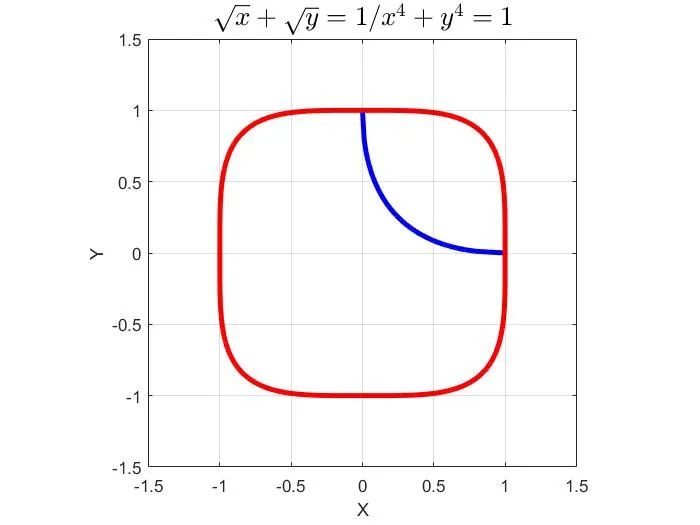
[题目](2022年，北京房山高三期末，10)某数学兴趣小组研究曲线C1：√x+√y=1和曲线C2：x⁴+y⁴=1的性质，下面是四位同学提出的结论：

甲：曲线C2关于原点对称；

乙：曲线C1,C2都关于直线y=x对称；

丙：曲线C1与坐标轴在第一象限围成的面积S1＞1/2；

丁：曲线C2与坐标轴在第一象限围成的面积S2＞π/4。

四位同学的结论中错误的是（  ）。

A)甲    B)乙    C)丙    D)丁

 

[答案]C

 

[解析]关于选项A：将曲线C1的方程，用x=-x，y=y替换，方程不变，所以选项A正确。

 

关于选项B：将曲线C1和曲线C2的方程，用y=x替换，方程不变，所以选项B正确。

 

关于选项C：曲线C1在第一象限围成的面积S1为边长为1的正方形减去半径为1的1/4圆，所以面积为，

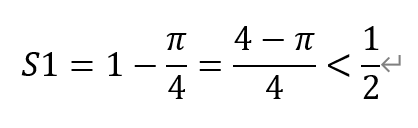
因此，选项C错误。

 

关于选项D：曲线C2在第一象限围成的面积大于1/4圆，所以面积S2＞π/4。因此，选项D正确。

 

综上，选项ABD正确，选项C错误。故选C。

 

[题目](2022年，北京房山高三期末，15)设函数

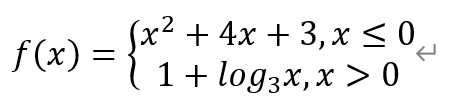
给出下列四个结论：

① 函数f(x)的值域是R；

② 对任意t＞0，方程f(x)=t都有3个实数根；

③ 存在x0∈R⁺，使得f(-x0)=f(x0)；

④ 若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3)，则x1+x2+x3的取值范围是(-35/9,5]。

其中所有正确结论的序号是        。

 

[答案]①③④

 

[解析]函数f(x)的图像，如图所示。

 

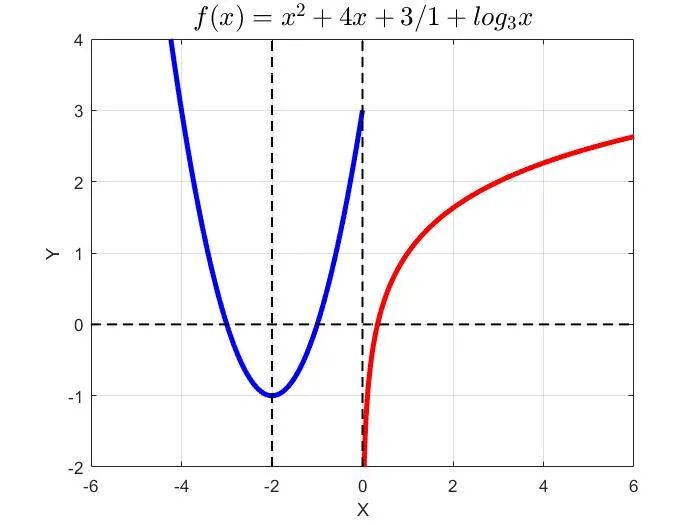
关于选项①：当x＞0时，对数函数的值域为R。所以函数f(x)的值域为R。因此，选项①正确。

 

关于选项②：对于t＞0，方程f(x)=t有3个实数根的取值范围为[-1,3]。因此，选项②错误。

 

关于选项③：当x≤0时，函数f(x)=x²+4x+3。其关于y轴对称的函数为f′(x)=x²+4x+3，其中x≥0。做出该函数的图像，与函数f(x)当x＞0时的图像有交点。因此，选项③正确。

 

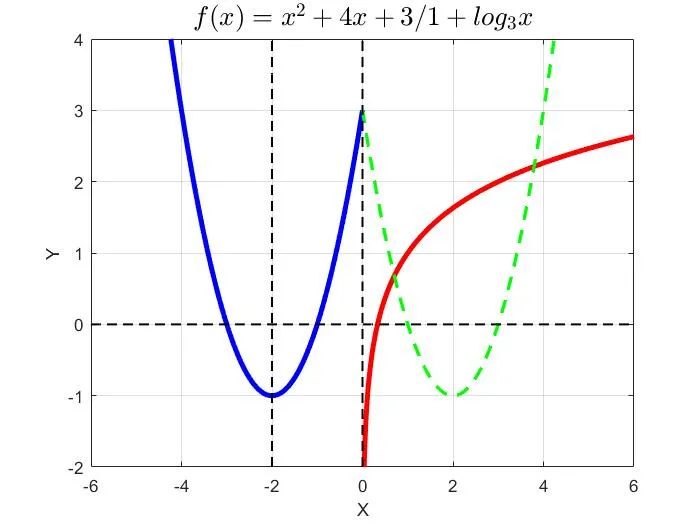
关于选项④：由②可知，若存在互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3)，则f(x)的取值范围为[-1,3]。

根据轴对称函数的性质可知，x1+x2=2x0=2×(-2)=-4。

对于方程1+log₃x=t，当t=-1时，有

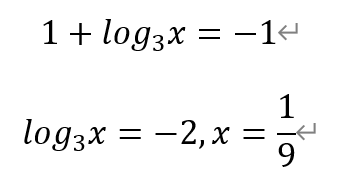
当t=3时，有

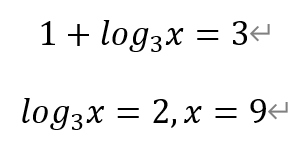
于是，x3的取值范围为(1/9,9]。从而，x1+x2+x3的取值范围为(-35/9,5]。因此，选项④正确。

 

综上，选项①③④正确，选项②错误。故填入①③④。