一、选择题：共10小题，每小题3分，共30分。在每小题列出的四个选项中，选出符合题目要求的一项。

1.下列直线中，倾斜角为锐角的是（  ）。

A)x-y+1=0    B)y=-2x+1   C)y=1    D)x=2

 

[答案]A

 

[解析]将直线x-y+1=0的方程变形得，y=x+1。斜率为1，倾角为45°，是锐角。故选A。

 

2.已知{an}为等差数列，且a1=1，a3+a4+a5=15，则a7=（ ）。

A)12    B)9   C)6    D)3

 

[答案]B

 

[解析]由a3+a4+a5=15得，3a4=15，a4=5。再次运用等差中项的性质，有2a4=a1+a7，即a7=2a4-a1=10-1=9。故选B。

 

3.抛物线y²=-8x的焦点F到准线l的距离为（  ）。

A)16    B)8   C)4    D)2

 

[答案]C

 

[解析]根据抛物线方程中p的几何意义，即焦点到准线的距离，可得p=4。故选C。

 

4.已知平面α,β的法向量分别为n1=(x,1,-1)，n2=(6,y,3)，且α∥β，则x+y=（  ）。

A)4/3    B)1   C)-3    D)-5

 

[答案]D

 

[解析]由于α∥β，所以

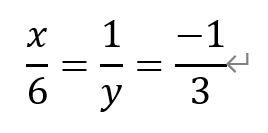
解得，x=-2，y=-3。因此x+y=5。故选D。

 

5.已知△ABC的三个顶点是A(-3,0)，B(6,2),C(0,-6)，则边AC上的高所在的直线方程为（  ）。

A)x+2y-2=0    B)x-2y-2=0

C)x-2y-4=0    D)2x+y-14=0

 

[答案]B

 

[解析]直线AC的斜率为，

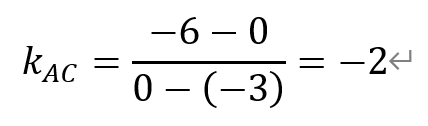
于是，AC边上的高的斜率为1/2。

根据直线方程的点斜式有，

即为x-2y-2=0。故选B。

 

6.设数列{an}的前n项和为Sn，若a2=7，a_n+1=a_n-4，n∈N^*，则S1，S2，S3，S4中，最大的是（ ）。

A)S1    B)S2   C)S3    D)S4

 

[答案]C

 

[解析]由a_n+1=a_n-4得，a_n+1=a_n=-4。于是数列{an}为等差数列，公差d为-4。=

利用拓展的通项公式，有

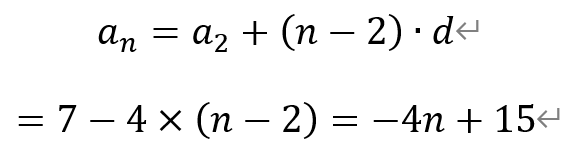
根据该通项公式，显然a3＞0，a4＜0。因此，前n项和Sn在n=3时取得最大值。故选C。

 

7.在长方体ABCD-A1B1C1D1中，AB=AD=4，AA1=3，点E,F分别在棱BB1，CC1上，EF∥AD1，BE=1/3BB1，则|B1F|=（  ）。

A)1    B)4/3   C)2    D)8/3

 

[答案]D

 

[解析]如图所示。由于AD1∥BC1，所以EF∥BC1。

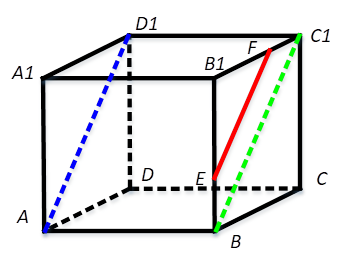
在面BCC1B1中，由于BE=1/3BB1，所以C1F=1/3C1B1。从而，

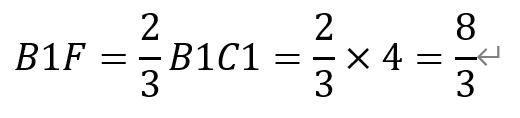
即值为8/3。故选D。

8.“a=2”是“圆(x-a)²+(y-b)²=4与y轴相切”的（ ）。

A)充分而不必要条件    B) 必要而不充分条件

C)充分必要条件    D)既不充分也不必要条件

 

[答案]A

 

[解析]当圆(x-a)²+(y-b)²=4与y轴相切时，可得a=±2。因此，a=2只是充分条件，而不是必要条件。故选A。

 

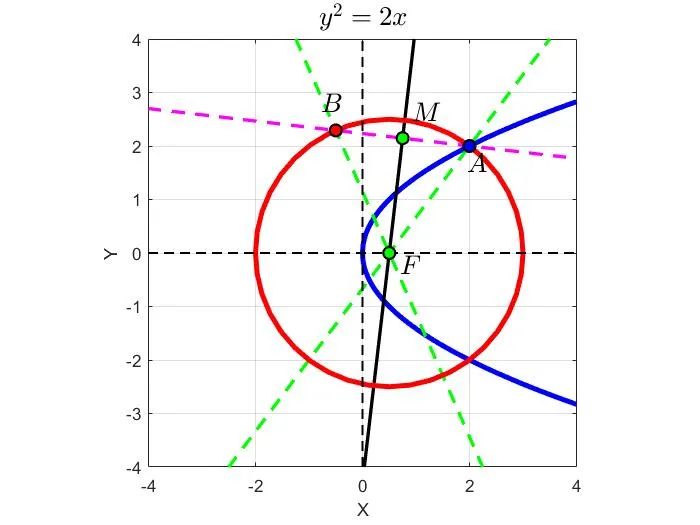
9.已知抛物线C：y²=2px(p＞0)过点A(2,2)，点B为平面直角坐标系平面内一点，若线段AB的垂直平分线过抛物线C的焦点F，则点B与原点O间的距离的最小值为（  ）。

A)√2    B)2   C)5/2    D)3

 

[答案]B

 

[解析]由于抛物线C：y²=2px(p＞0)过点A(2,2)，所以代入点A的坐标，解得p=1。于是点F(1/2,0)。

设点B(x0,y0)。则AB中点

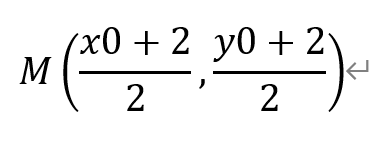
由于F在AB的中垂线上，所以FM•AB=0，

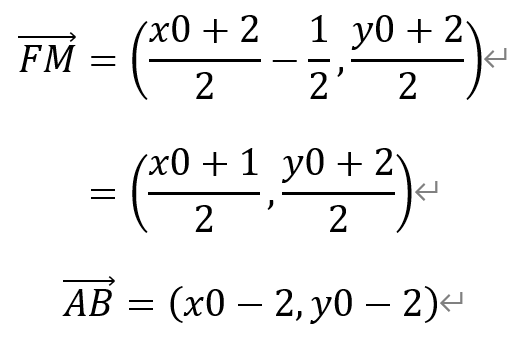
即有

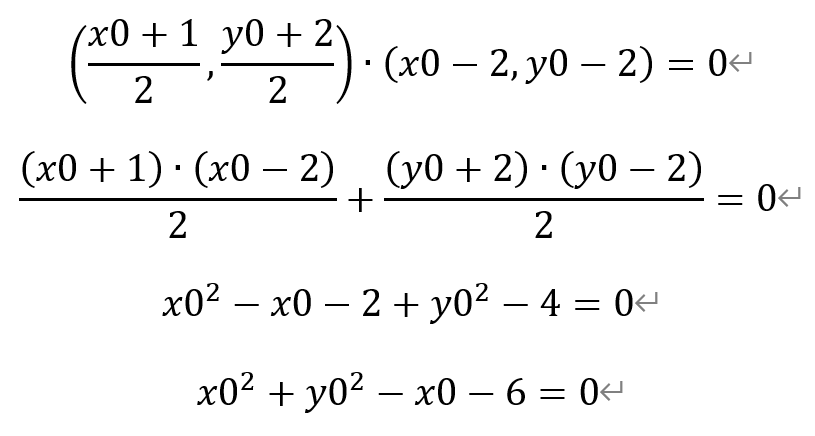
其轨迹为一个圆，配方得

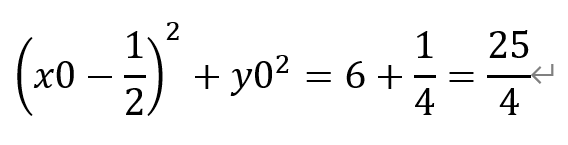
该圆的圆心为F(1/2,0)，半径r为5/2。

因此，它与原点O间的距离的最小值为

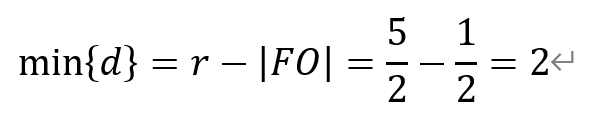
即值为2。故选B。

 

10.均匀压缩是物理学一种常见现象.在平面直角坐标系中曲线的均匀压缩，可用曲线上点的坐标来描述.设曲线C上任意一点P(x,y)，若将曲线C纵向均匀压缩至原来的一半，则点P的对应点为P1(x,1/2y).同理，若将曲线C横向均匀压缩至原来的一半，则曲线C上点P的对应点为P2(1/2x,y).若将单位圆x²+y²=1先横向均匀压缩至原来的一半，再纵向均匀压缩至原来的1/3，得到的曲线方程为（  ）。

A)x²/4+y²/9=1    B)x²/9+y²/4=1

C)4x²+9y²=1    D)9x²+4y²=1

 

[答案]C

 

[解析]将单位圆x²+y²=1横向均匀压缩至原来的一半，有

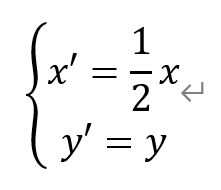
再纵向均匀压缩至原来的1/3，有

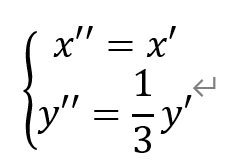
于是有，

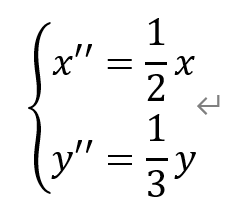
即

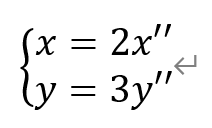
代入单位圆的方程，得

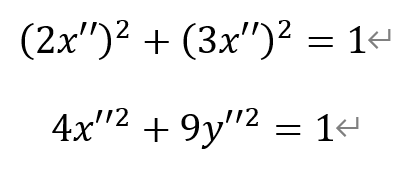
将变量换回x,y，得4x²+9y²=1。故选C。

 

二、填空题：共6小题，每小题4分，共24分。

11.若过点O(0,0)和M(1,3)的直线与直线ax-y-2=0平行，则a=        ．

 

[答案]3

 

[解析]直线OM的斜率为

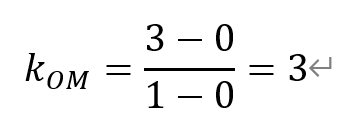
将直线ax-y-2=0的方程变形，得y=ax-2。根据两条直线的平行关系，可知a=3。故填入3。

 

12.写出一个离心率e=2且焦点在x轴上的双曲线的标准方程        ,并写出该双曲线的渐近线方程        ．

 

[答案]x²-y²/3=1；y=±√3x。(答案不唯一)

 

[解析]根据双曲线离心率和渐近线斜率的关系，有

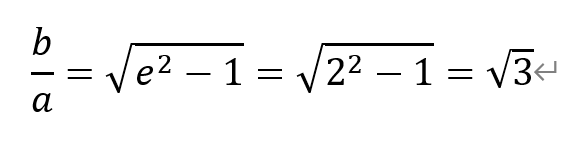
下略。

 

13.已知数列{an}满足

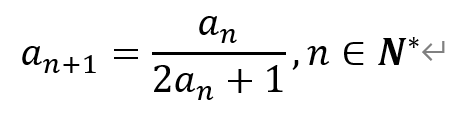
若a3=1/7，则a1=        ．

 

[答案]1/3

 

[解析]将所给表达式取倒数，有

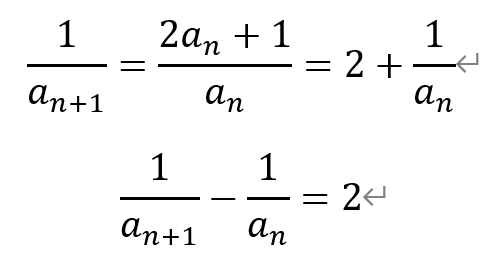
即数列{1/an}为公差为2的等差数列。

由于a3=1/7，所以1/a3=7。从而有，1/a2=5,1/a1=3。即a1=1/3。故填入1/3。

 

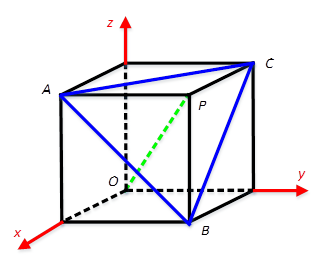
14.已知点M(-1,2,0)，平面α过A(1,0,1)，B(1,1,0)，C(0,1,1)三点，则点M到平面α的距离为        ．

 

[答案]√3/3

 

[解析]如图所示。可见平面α即平面ABC，其中OP⊥面ABC。因此面ABC的法向量为(1,1,1)。

取点A(1,0,1)。则根据平面方程的点法式，可知面ABC的方程为，

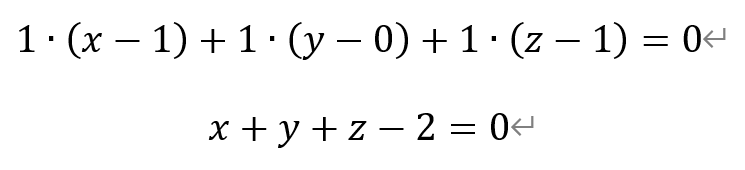
再利用点到平面的距离公式，有

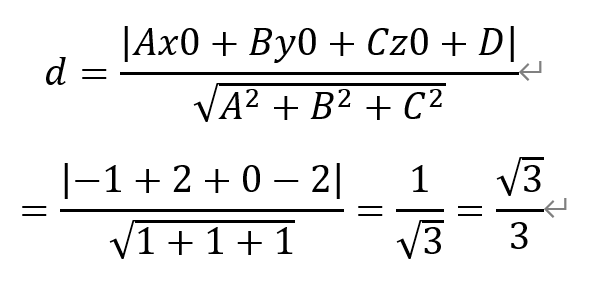
即值为√3/3。故填入√3/3。

15.1970年4月我国成功发射了第一颗人造地球卫星“东方红一号”，这颗卫星的运行轨道是以地心(地球的中心)为一个焦点的椭圆.已知卫星的近地点(离地面最近的点)距地面的高度约为439km，远地点(离地面最远的点)距地面的高度约为2384km，且地心、近地点、远地点三点在同一直线上，地球半径约为6371km，则卫星运行轨道是上任意两点间的距离的最大值为        km．

 

[答案]15,565

 

[解析]如图所示。近地点距离地面的高度为AM，远地点距离地面的高度为BN。F为地心，即卫星椭圆轨道的一个焦点。则AF=a-c，BF=a+c。

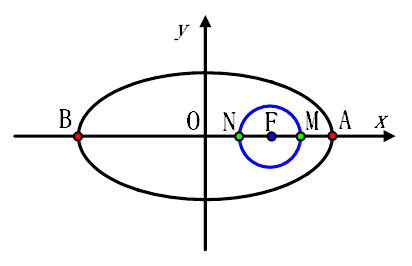
考虑到地球半径，于是椭圆中的长轴长为，

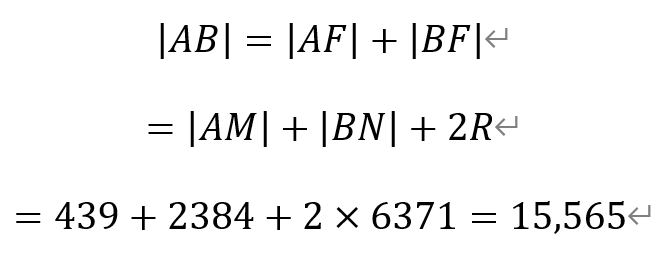
即值为15565。故填入15565。

16.如图，在棱长都为1的平行六面体ABCD-A1B1C1D1中，AB，AD，AA1两两夹角均为π/3，则AC1•BD=________；请选择该平行六面体的三个顶点，使得经过这三个顶点的平面与直线AC1垂直.这三个顶点可以是________．

 

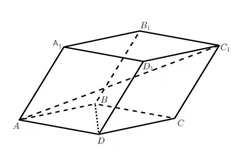
[答案]0；A1,B,D或者B1,D1,C。

 

[解析]根据空间向量的合成，有

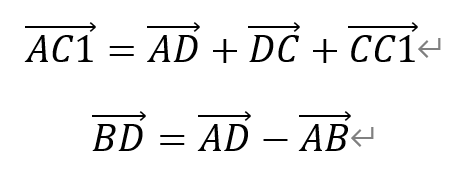
于是，AC1•BD为

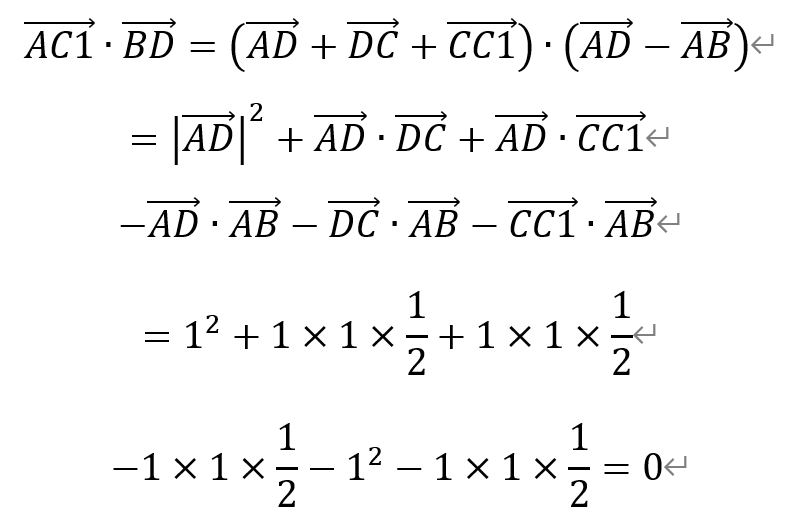
其中需要注意的是，两个向量之间的夹角要考虑共起点的情况。如果不是共起点，需要进行平移。例如∠ADC=2π/3，但是AD和DC之间的夹角为π/3。

由于底面ABCD为菱形，所以AC⊥BD。又由前述AC1•BD=0可知，AC1⊥BD，AC∩AC1=A，因此BD⊥面ACC1。根据面面垂直的判定定理，面A1BD⊥面ACC1。进而可得AC1⊥面A1BD。类似的，可以证明AC1⊥面B1D1C。

故分别填入0，以及A1,B,D或者B1,D1,C。