[题目](2022年，北京丰台高三期末，10)已知函数

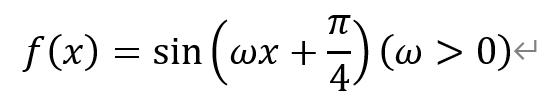
在区间[0,π]上有且仅有4条对称轴，给出下列四个结论：

① f(x)在区间(0,π)上有且仅有3个不同的零点；

② f(x)的最小正周期可能是π/2；

③ ω的取值范围是[13/4,17/4)；

④ f(x)在区间(0,π/15)上单调递增.

其中所有正确结论的序号是（  ）。

A)①④    B)②③    C)②④    D②③④

 

[答案]B

 

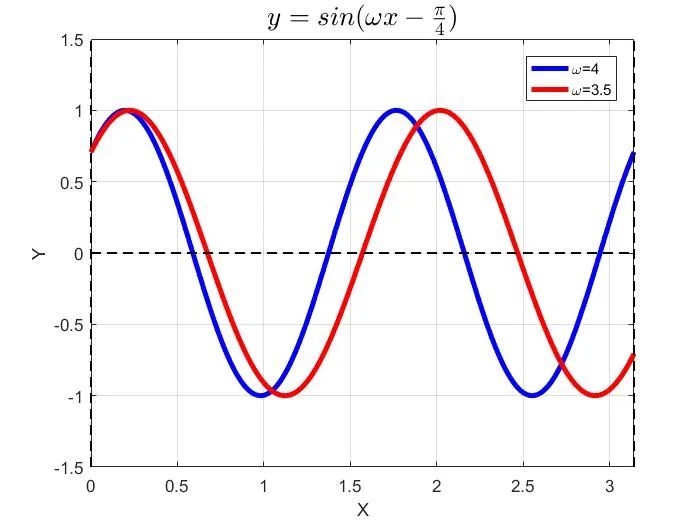
[解析]关于选项①：虽然函数f(x)在[0,π]上包含四条对称轴，但是随着ω的变化，在第4条对称轴后，可能包含相邻的下一个对称点。

 

例如，当ω=4时，函数f(x)在[0,π]上有四个零点；当ω=3.5时，函数f(x)在[0,π]上有三个零点。如图所示。因此，选项①错误。

 

关于选项②：若函数f(x)的最小正周期为π/2，则

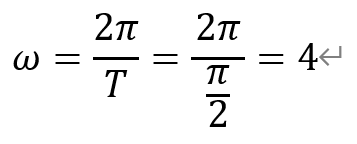
即ω=4。如上图所示。因此，选项②正确。

 

关于选项③：函数f(x)的对称轴为，

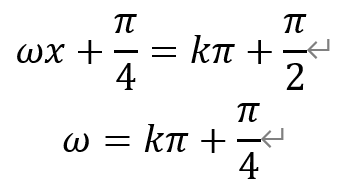
其中k∈Z，且k≥0。

关于ω的取值范围，下限为：x=π是它的第四条对称轴，即

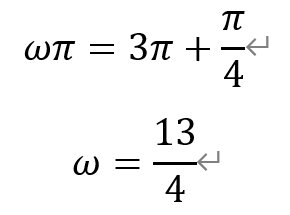
上限为：x=π是它的第五条对称轴(该上限取不到)，即

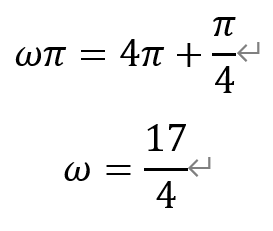
于是，ω的取值范围为[13/4,17/4)。因此，选项③正确。

 

关于选项④：当x∈(0,π/15)时，有

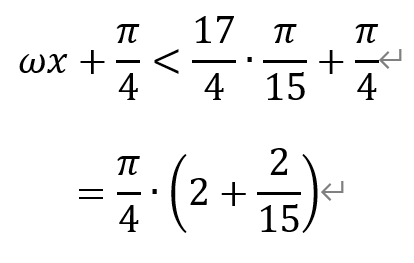
该值已经超过π/2，进入单减区间。因此，选项④错误。

 

综上，选项②③正确，选项①④错误。故选B。

 

[题目](2022年，北京丰台高三期末，15)已知点P(2,0)和圆O：x²+y²=36上两个不同的点M，N，满足∠MPN=90°，Q是弦MN的中点，给出下列四个结论：

① |MP|的最小值是4；

② 点Q的轨迹是一个圆；

③ 若点A(5,3)，点B(5,5)，则存在点Q，使得∠AQB=90°；

④ △MPN面积的最大值是18+2√17。

其中所有正确结论的序号是        。

 

[答案]①②④

 

[解析]关于选项①：对于圆O上的任意一点M，都可以做出PN⊥PM，与圆交于点N和N′。其中点P与圆O上的点的最小距离为6-2=4。因此，选项①正确。

 

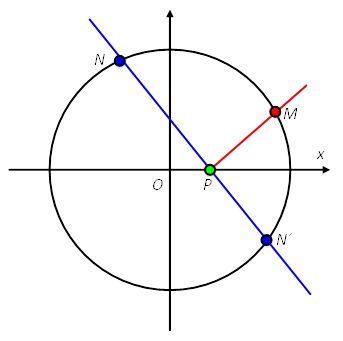
关于选项②：设点Q(x,y)。如图所示。

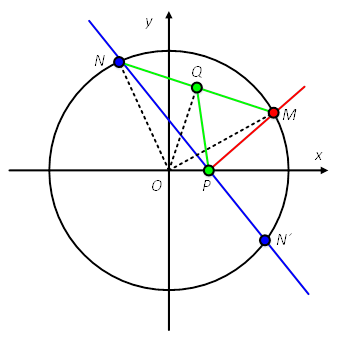
在Rt△MPN中，点Q为斜边MN的中点。于是有，

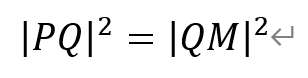
连接OM，ON。由于OM=ON=6，所以△MON为等腰三角形。Q为MN中点，根据等腰三角形的性质，OQ即为边MN上的高，即OQ⊥MN。于是，根据勾股定理，有

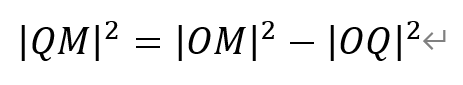
从而有，

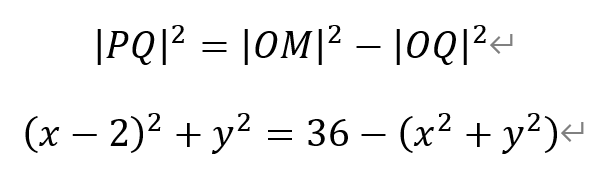
整理得，

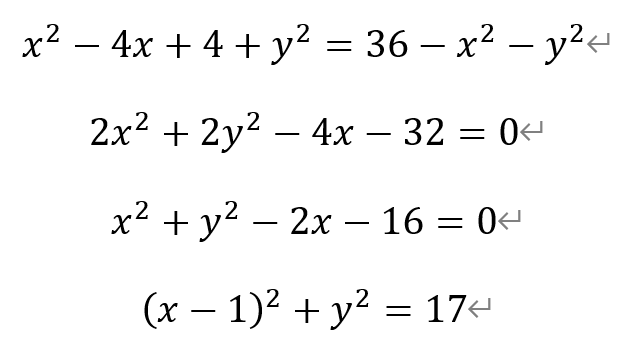
即点Q的轨迹是圆心为S(1,0)，半径r1为√17的圆。因此，选项②正确。

 

关于选项③：以点A(5,3)，点B(5,5)为直径的圆，圆心T为(5,4)，半径r2为1。两个圆的圆心距|ST|为

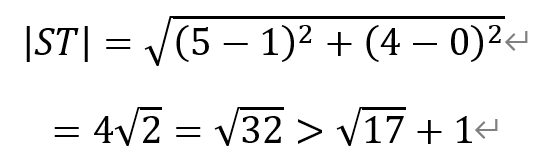
即圆S与圆T相离，两个圆没有交点。于是在圆S上不存在点Q，使得∠AQB=90°。因此，选项③错误。

 

关于选项④：当点M和点N的连线垂直于x轴，且都位于y轴的左侧时，△MPN的面积最大。如图所示。

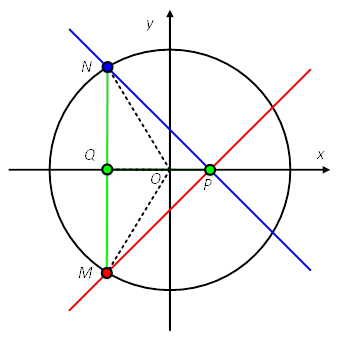
此时，点Q的坐标为(-√17+1,0)。于是，

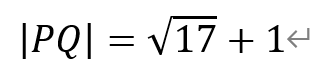
△MPN的面积为

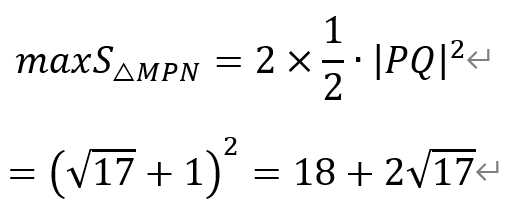
即值为18+2√17。因此，选项④正确。

 

综上，选项①②④正确，选项③错误。故填入①②④。