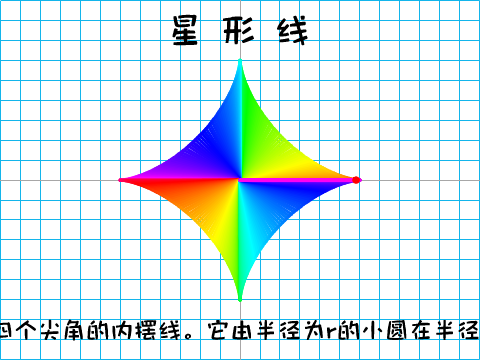
[题目](2022年，北京石景山高三期末，10)如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E,F，且EF=1/2，给出下列三个结论：

① AC⊥BE；

② △AEF的面积与△BEF的面积相等；

③ 三棱锥A-BEF的体积为定值；

其中，所有正确结论的个数是（ ）。

A)0    B)1    C)2    D)3

 

[答案]C

 

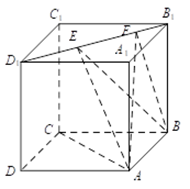
[解析]关于选项①：连接BD。由于AC⊥BD，AC⊥DD1，且BD∩DD1=D，所以AC⊥面BDD1B1。BE在面BDD1B1内，所以AC⊥BE。因此，选项①正确。

关于选项②：由于|EF|=1/2，为定值，所以△AEF和△BEF的面积取决于点A和点B到直线B1D1的距离。其中点A到直线B1D1的距离为

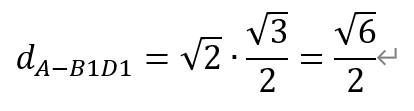
而点B到直线B1D1的距离为1。于是，它们的面积不相等。因此，选项②错误。

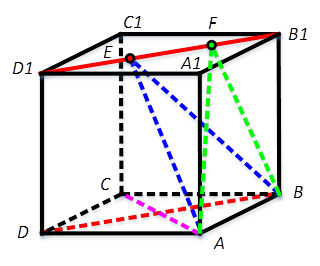
关于选项③：连接DE。可以将三棱柱ABD-A1B1D1分割为：

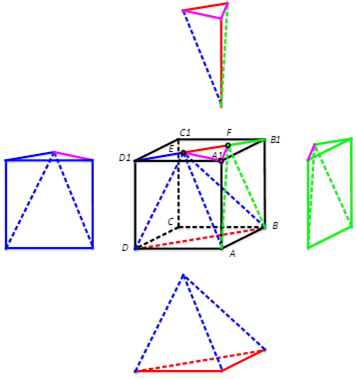
四棱锥E-AA1D1D(左侧)、四棱锥F-AA1B1B(右侧)、三棱锥A-A1EF(上方)、三棱锥E-ABD(下方)和三棱锥A-BEF(未单独标出)。

其中，由于底面积和高不变，三棱锥A-A1EF和三棱锥E-ABD的体积为定值。

四棱锥E-AA1D1D和四棱锥F-AA1B1B的底面积相等且不变，它们到底面的高分别为EG和FH。其平面图如图所示。

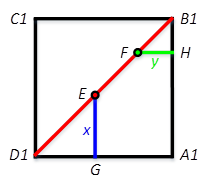
由于△EGD1和△FHB1都是等腰直角三角形，所以

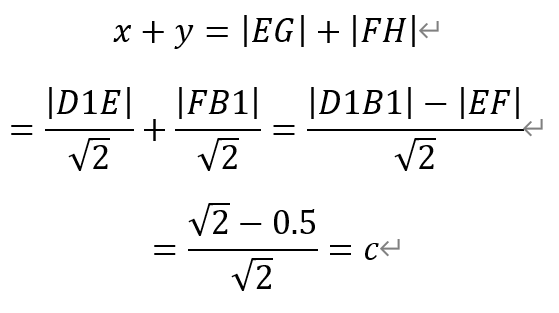
即它们的高线之和为定值，从而四棱锥E-AA1D1D和四棱锥F-AA1B1B的体积为定值。

于是，三棱锥A-BEF的体积为定值。因此，选项③正确。

 

综上，选项①③正确，选项②错误。故选C。

  

[题目](2022年，北京石景山高三期末，15)数学中有许多形状优美的曲线，如星形线，让一个半径为r的小圆在一个半径为4r的大圆内部，小圆沿着大圆的圆周滚动，小圆的圆周上任一点形成的轨迹即为星形线．如图，已知r=1，起始位置时大圆与小圆的交点为A(A点为x轴正半轴上的点)，滚动过程中A点形成的轨迹记为星形线C．有如下结论：

① 曲线C上任意两点间距离的最大值为8；

② 曲线D：|x|+|y|=4的周长大于曲线C的周长；

③ 曲线C与圆x²+y²=4有且仅有4个公共点．

其中正确的序号为        ．

 

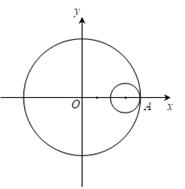
[答案]①③

 

[解析]星形线得名于希腊文的星星，是有四个尖角的内摆线，属于超椭圆的一种。它的直角坐标方程为，

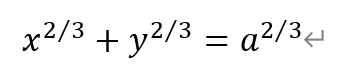
参数方程为，

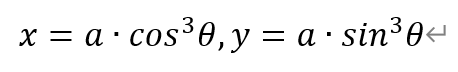
现实生活中，公共汽车的折叠门就是其典型应用：开门时一扇门折拢成为半扇，关门时又重新伸展成一扇。门轴在滑槽中的运动轨迹就是星形线。

 

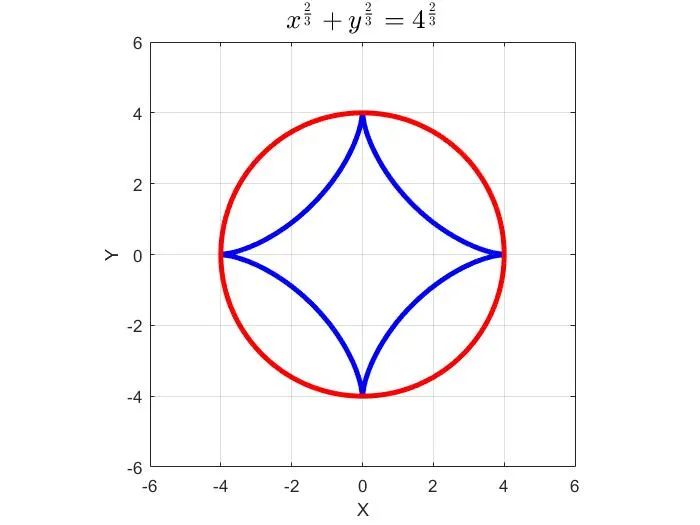
关于选项①：由于r=1，所以a=4r=4。于是，曲线C上任意两点间距离的最大值为8。因此，选项①正确。

 

关于选项②：星形线在半径为a的大圆内的周长为6a。本题中a=4，于是弧长为24；曲线D：|x|+|y|=4在第一象限的边长为4√2，整个闭合曲线的长度为16√2。从而有，

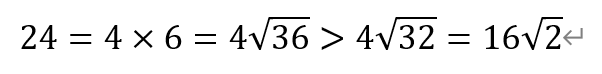
即曲线C的周长大于曲线D的周长。因此，选项②错误。

 

关于选项③：曲线C与圆x²+y²=4有且仅有4个公共点。因此，选项③正确。

 

综上，选项①③正确，选项②错误。故填入①③。

 

 

[附录]星形线周长的计算。

 

设生成大圆的半径为a。由于星形线关于两个坐标轴对称，所以只需计算第I象限的部分即可。

 

星形线的参数方程为，

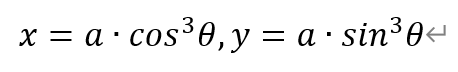
分别对θ求导，得

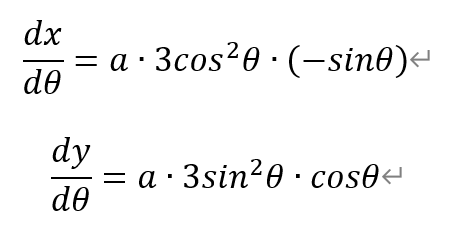
于是，其在第I象限的弧长为，

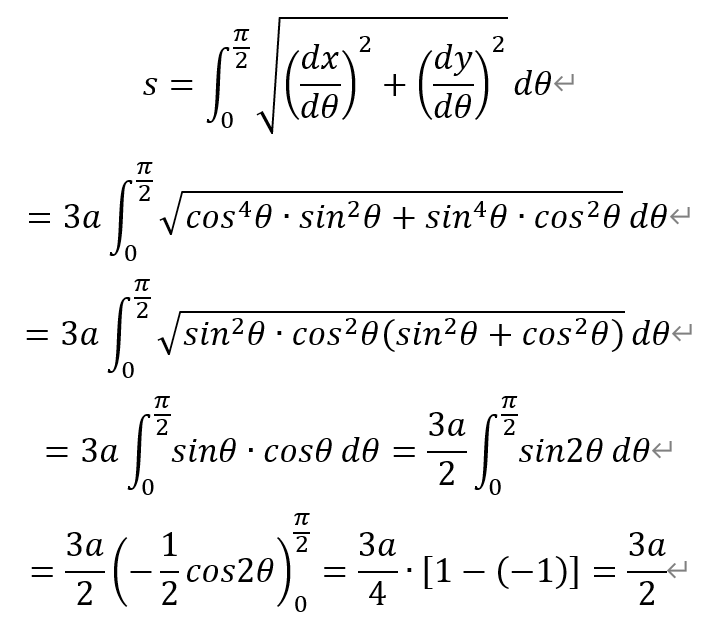
从而，星形线的周长为，

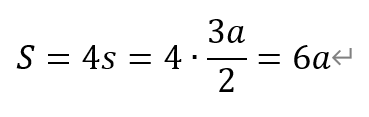
即值为6a。