众所周知，AMC 8主要拉开分数都在最后的几道题，前面的一般难度不大。这里我们一起来看看今年的AMC 8出题人是如何为难同学们的。
1-9这9个数字，分别三个三个组合起来，每组数字加起来相等。这样的组合总共有多少种？已知 1+2+...+9 = 45，那么每一组的总和就是45/3=15。我们首先用最大的数字9来看，当这一组中包含9的时候，只有两个组合（9, 1, 5）和（9,2,4）。
然后我们再用包含8，加起来和为15的分类来对一下：很显然，每组之下只有一个组合符合标准。也就是说，当有一组为(9,1,5)的时候，剩下符合条件的就只能是(8, 3, 4) 和（7,2,6）；当有一组为(9,2,4)时候，剩下两组就一定是(8,1,6)和(7,3,5)。因此，所有的组合只有两种，选(C)。
一个正整数数列，第三项开始，数字是前面两项的乘积。数列中第6项是4000，请问第一项是多少？
根据题目，已知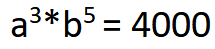 
此时心算能力强的估计可以得到答案了，不强也没关系：问a是多少，就拿选项去印证一下啊，显然可以排除（a=1)，(a=2), (a=4)，到（a=5)时，运气来了：5*5*5 = 125; 4000/125 = 32 = 2*2*2*2*2 ；因此a=5，b=2，选（D）。
在3*3的格子里，随机放入四种小方块，请问最后形成的图案中，包括一个大的2*2菱形（图示了一种）的概率有多大？首先我们来看形成一个菱形的概率是 (1/4)*(1/4)*(1/4)*(1/4)
显而易见，在3*3方格中有4种情况摆放一个2*2的菱形（左上,右上,左下.右下），所以总的概率是：
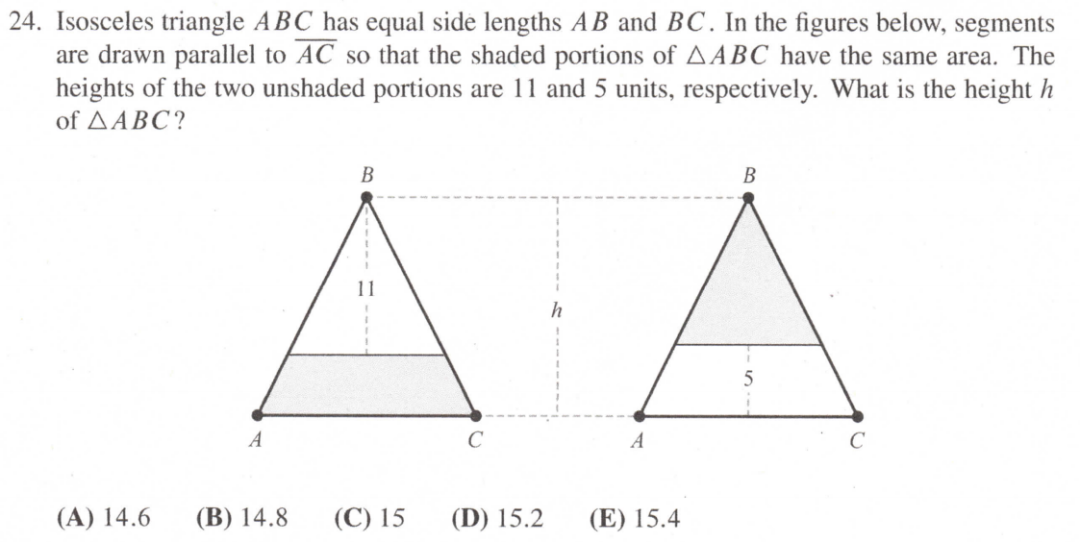
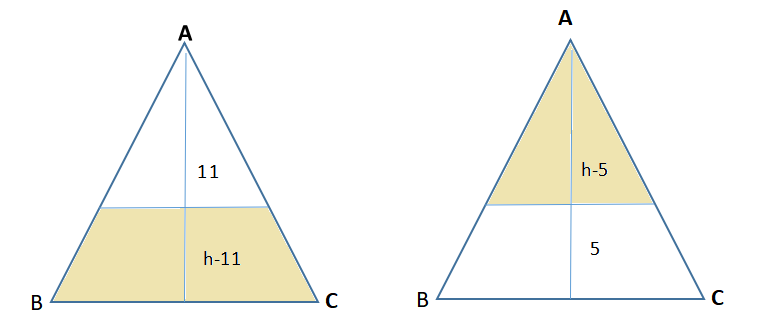
(1/4)*(1/4)*(1/4)*(1/4)*4 = 1(4*4*4) = 1/64 选（C）(此题说明了当你没有把握的时候，选C蒙对的可能性大一点)已知ABC为等腰三角形，在图中做了两条AC的平行线，使得两个图形中的阴影面积相等，即左边梯形面积和右边小三角形相等。已知左边空白部分高为11，右边空白部分高为5，求三角形ABC的高h
设左侧阴影面积为S1，右侧阴影面积为S2。先来回顾一下相似三角形的面积比知识：【相似三角形定理】相似三角形的对应角相等，对应边成比例。相似三角形任意对应线段的比等于相似比，相似三角形的面积比等于相似比的平方。
我们记大三角形ABC面积为S，左侧梯形阴影面积为S1，右侧三角形阴影面积为S2，下图可以得出：(选C的同学不要怪我啊，说实话这个15的整数值很有欺骗性...)15个数构成等差数列，其中第1个数在1和10之间，第3个数在13和20之间，第15个数在241和250之间。求第14个数的各位数字之和；
为了求出公差d，我们要想办法消去a1。将(1)取负，可以得到：
将d=17代入(2):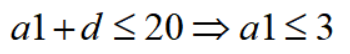 
将d=17代入(3)：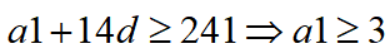
综合以上：a1 = 3 a14=3+13*17 = 224
最后我们得到a14=224，三位数总和为8，选A
以上，是2023年AMC 8数学竞赛最后5题的分享，如果小伙伴有更好的解法欢迎分享，谢谢啦~
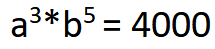
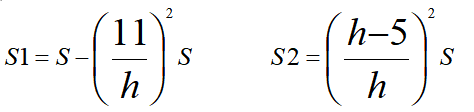
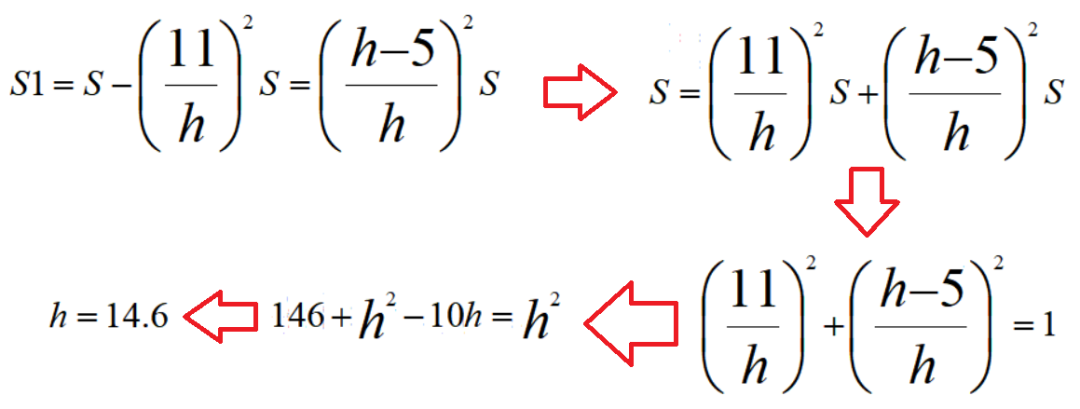
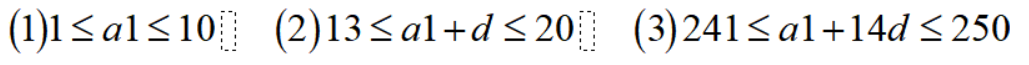
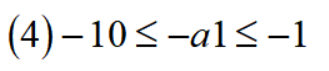
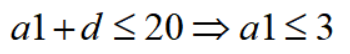
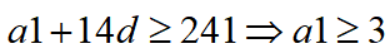
全部 0条评论